圆锥曲线求值问题中的奇思妙解
2015-09-11 18:42杨美
新课程·中学 2015年7期
杨美
在圆锥曲线数值问题中,如何结合题目条件,根据圆锥曲线的定义、性质以及相应的思维方法来分析与处理是解决问题的关键.下面结合实例就圆锥曲线中数值问题的巧解加以实例剖析.
一、妙用定义,巧求未知量
圆锥曲线的定义揭示的是各对应的曲线的本质属性.对于涉及的圆锥曲线中的参数问题,若能巧妙灵活应用定义,往往能达到化繁为简、事半功倍的效果.
例1.已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点M(-3,m)到焦点距离等于5,求抛物线的方程和m的值.
分析:解答本题可以直接利用抛物线的定义,得点M到准线的距离为5,直接得出有关p的关系式,从而求出p的值.
点评:本题涉及直线与抛物线的位置关系中的变量的取值范围问题,通过方程有不等实根的充要条件的转化,巧妙地把几何问题转化为代数问题,从而达到求解参数的取值范围的目的.构思新颖,方法巧妙.
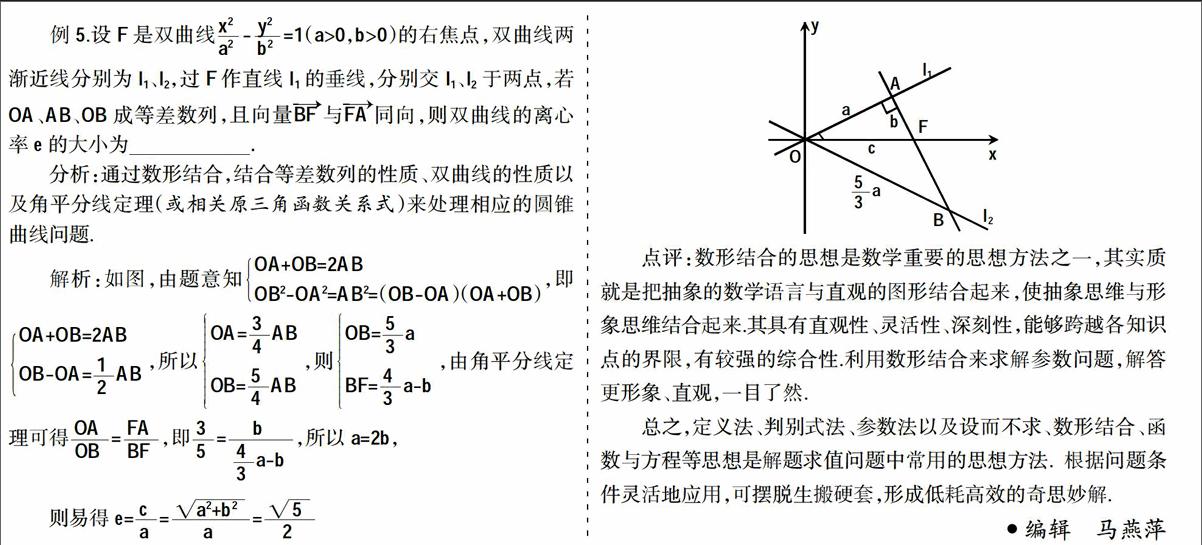
五、数形结合,巧求离心率
著名数学家华罗庚说过:“数形本是两相倚,焉能分作两边飞.数缺形时少直观,形少数时难入微.”在圆锥曲线中的许多基本量都具有一定的几何意义,挖掘题目中的隐含条件,揭示图形的几何性质,采用数形结合的思想方法,可解决一些相应的参数问题.
点评:数形结合的思想是数学重要的思想方法之一,其实质就是把抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维结合起来.其具有直观性、灵活性、深刻性,能够跨越各知识点的界限,有较强的综合性.利用数形结合来求解参数问题,解答更形象、直观,一目了然.
总之,定义法、判别式法、参数法以及设而不求、数形结合、函数与方程等思想是解题求值问题中常用的思想方法.根据问题条件灵活地应用,可摆脱生搬硬套,形成低耗高效的奇思妙解.
编辑 马燕萍
猜你喜欢
初中生学习指导·中考版(2023年9期)2023-09-30
中学生数理化·七年级数学人教版(2022年4期)2022-04-26
理科爱好者(教育教学版)(2022年1期)2022-04-14
中学生数理化·七年级数学人教版(2021年4期)2021-07-22
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
新高考·高二数学(2017年9期)2018-03-16
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16