习题教学中培养学生问题意识的几点做法

黄天星

问题意识是指思维的问题性心理。学生的问题意识主要是指在学习中会遇到一些不明白的问题或者是现象，产生疑问、探求的心理状态，是对学习中的问题进行质疑、思考、探讨、反思的心理品质。

爱因斯坦有一句名言：“提出一个问题往往比解决一个问题更为重要。”亚里士多德曾说：“一切真正有所作为的人，都是具有强烈问题意识的人。”

习题教学本应该是培养学生问题意识的主阵地，事实是怎样的呢？“老师滔滔不绝，学生昏昏欲睡”，课堂上只剩下老师的声音，学生更多的是“被问”，而不是“提问”，更多的是“求同”，而不是“存异”。美籍华裔物理学家、诺贝尔物理学奖获得者李政道指出：“我们的教师是在教学生做学答，而不是做学问。”那么，怎样在习题教学中培养学生的问题意识呢？这是值得一线教师思考的问题。对此，我做了以下尝试。

一、利用变式训练培养问题意识

所谓“变式”，是指老师有目的、有计划、有意识地给出一个题干，让学生讨论、交流，思考如何对命题进行合理的转变或转化，以期达到举一反三、触类旁通的目的。

通常，习题变式可以从改变条件、改变设问、改变物理模型三个方面进行。

例题1：如图1所示，设带电粒子质量为m，电量为q（q>0），以速度v垂直电场线方向沿两极板中心线射入匀强电场。已知两极板电势差为u，板长为L，两板间距离为d（不计重力）。

图1

以上是典型的带电粒子在电场中运动的基本题干，根据题干所给条件就可以编写很多设问，例如：

1.带电粒子在电场中的加速度是多少？

2.带电粒子在电场中运动的水平位移是多少？

3.带电粒子在电场中运动的时间是多少？

4.带电粒子出电场时的侧移是多少？

5.带电粒子出电场时的速度是多少？

学生编写设问可以训练逻辑思维能力、归纳总结能力，对题干的准确阅读和理解，并能明白各个已知物理量之间的关系及适用的物理规律，从而学会提出问题。

本题在“条件”上也可以做适当的补充和修改，例如：

1.如果是负电荷，则粒子如何偏转？

2.如果带电粒子恰好出电场，侧移距离是多少？

3.如果带电粒子不能出电场，则粒子经过多长时间打在极板上？

学生练习编写、修改、补充条件可以训练审题、读题能力，特别是：①对特殊字、句、条件的理解和隐含条件的挖掘能力，如“刚好”“这个实验说明了”“静止”“匀速圆周运动”“光滑平面”“不损失机械能”等;②对无关条件（干扰因素）的排除能力，如要用正对面积的题给出物体面积（它们不一定相等），计算静摩擦力的题给出动摩擦系数μ等;③对多解条件的审理能力，如矢量方向引起的多解、周期性導致的多解等。

在“模型”上可以进行以下变换或迁移：

1.如果带电粒子从静止开始经过一电压为u的加速电场加速后再进入偏转电场，则带电粒子离开电场时的速度、侧移、偏转角各是多少？

2.若有一个荧光屏与偏转电场水平距离为s，则带电粒子打在荧光屏上的亮点与屏中心间的距离是多少？

习题变式使一题多用、多题重组，给人新鲜、生动的感觉，能唤起学生的好奇心和探求欲，虽然变换了问题的条件、结论或形式，但不改变问题的本质。学生从“变”中发现“不变”的本质，从“不变”中探究“变”的规律，全方位、多角度、多渠道地思考问题，多探讨、多争论，在无穷的变化中领略物理的魅力，有效训练学生的思维创造性，培养学生的问题意识和创新意识。

二、利用错误结论培养问题意识

“结论法”曾一度成为大家学习物理的“捷径”，但在学习中也产生一些似是而非，真真假假的结论，许多老师和学生又因为受其害而避之，其实这些错误结论是不可多得的“问题素材”，在培养学生的问题意识中收到意想不到的效果。例如，在“瞬间加速度”的教学中就常有“弹簧的弹力瞬间不会突变”这一悖论。

首先，我先给出题目：

例题2：如图2，质量均为m的物体用一根轻弹簧AB连接，并用细绳OA悬挂在天花板上，若用火将细绳烧断，则在绳刚断的这一瞬间，物体的加速度是（    ）

图2

A.a=0    B.a=g/2    C.a=g    D.a=2g

然后让学生思考解答，并有意识地提醒大家用“结论法”，目的是先让学生掉入“陷阱”。结果，大多数学生选了A。我追问了理由，学生的回答是：当烧断绳子这一瞬间，因为“弹力在瞬间不可突变”，物体所受合力依然为零，则瞬间加速度自然也为零。

紧接着，我告诉大家正确答案是C。瞬间安静后就是一阵哗然，显然，学生已经产生“疑问”，我顺势抛出：“这是为什么呢？”学生开始交流、讨论、争辩。

最后，我做出如下解释：在高中阶段，轻弹簧就是指质量为零的弹簧，是理想化的模型。当轻弹簧的两端都固定有质量不为零的物体时，是处于“受约束”状态，弹簧的弹力不会突。当轻弹簧的两端或其中一端不再固定时，处于“解除约束”状态，弹簧的弹力就会发生突变。

例题2中，起初，弹簧两端都受约束，在绳子被烧断瞬间，弹簧的A端解除了约束，弹力瞬间变为零，物体只受重力作用，所以瞬间加速度a=g，方向是竖直向下。

三、利用知识拓展培养问题意识

受种种因素的影响，高中物理教材中有一些内容是“欲言又止”，没有解释到位。这部分内容往往搅乱学生的思维，学生因为不知道“是什么问题”，当然没办法“提出问题”，更不可能“解决问题”，“问题意识”自然就没了。这是一个很尴尬的问题，当然这是一线物理教师在教学中必须注意的问题。我认为，适当地拓展和补充是有必要的，毕竟完整的知识体系对培养学生的问题意识是十分重要的。

例如，关于“感应电流”，在高中物理教材中，并没有感生和动生之说，只是笼统地称之为感应电流。对感应电流产生的条件就只学习“磁通量发生变化”这一种情况，大多数学生都会产生“只有磁通量发生变化才会产生感应电流”的错误认识。

对此，我用下面一道题拓展和释疑。

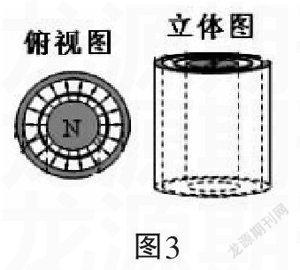
例题3：如图3所示，一个很长的竖直放置的圆柱形磁铁，产生一个辐射状的磁场，磁场水平向外。磁极狭缝间某点的磁感应强度与该点到圆柱形磁极中心轴的距离成反比。圆形单匝线圈从某高度无初速释放，线圈平面始终水平且保持与圆柱形磁极共轴。线圈被释放后（    ）

图3

A.线圈中没有感应电流，线圈做自由落体运动

B.在俯視图中，线圈中感应电流沿逆时针方向

C.线圈半径越大，线圈的最大速度就越小

D.线圈半径越大，线圈的最大速度就越大

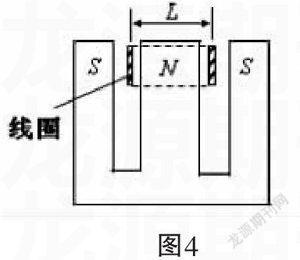
首先，大家进行交流与讨论，然后一起画出这个装置的纵截面图（如图4）。再引导学生画出这个辐射状磁场的磁感线分布示意图（如图5）。

图4                                      图5

从图4、图5可以看出，线圈在下落过程中，磁感线始终与线圈平行，磁通量没有变化。那线圈中有没有感应电流呢？

继续引导学生思考：线圈在下落过程中，有没有切割磁感线？切割会不会产生感应电流？大家再一次进行交流、讨论、争辩，大家众口不一，各执己见。

至此，学生的思维和问题意识都被激活，发挥得淋漓尽致。

接着，我再适时补充感生电流与动生电流的知识，得出“闭合线圈中的磁通量发生变化时，产生感生电流;做切割磁感线运动时，产生动生电流”。

以上是我在习题教学中培养学生问题意识时常用的做法。美国现代心理学家布鲁姆说：“最精湛的教学艺术，遵循的最高准则就是让学生提问题，让学生学会提问。”只要我们用心，就能找到许许多多培养问题意识的途径和方法，学生的奇思异想、独立见解就会层出不穷，学生就能变“怕问”为“敢问”，并向“会问”、“善问”和“乐问”发展。