关于平面机构自由度的思考

岳彩青

摘 要： 机构自由度是机构具有独立运动的参数，是机械设计和分析中重要的概念，针对分析机构自由度时出现的问题，说明机构自由度公式的应用范围及需注意的问题，并基于此提出思考，以便更好地运用和掌握。

关键词： 机械设计 机构 自由度 独立运动

引言

机构具有确定运动时所必须给定的独立运动参数的数目，称为机构的自由度[1]。机构自由度计算问题，无论在《机械原理》课程中还是在实际机械的设计和分析中都占有重要地位。常规设计的机构，其运动必须是确定的；一个运动链是否成为机构不仅取决于其结构，还取决于其原动件数目，机构具有确定运动的条件是：机构的自由度数（以F表示）等于机构给定的原动件数（以s表示），即S=F且F>0；故自由度计算正确与否将会引起机构确定运动分析结果的正确，它是机构设计必需的步骤。所以机构的自由度计算在机构的设计中占有很重要的地位。早在19世纪中后期，德、俄等国学者已开始对机构的组成要素、组成方式及分类方法等问题进行研究，提出的诸如运动副等基本概念、机构自由度等基本方法一直沿用至今[2]。我国现行的教材无一例外采用1869 年由俄国科学院院士契贝舍夫（Grübler-Kutzbach）提出的契氏公式计算平面机构的自由度。即

F=3n-2■-p■ （1）

其中n为活动构件数，p■ 为低副数，p■为高副数

但是，在用此公式分析一些平面机构如全移动副平面机构时出现错误的结论，与实际情况不符。基于此，笔者对公式应用条件、注意事项等进行了研究并提出了几点思考。

1.契氏公式的应用条件

契氏公式应用到现在已近150年的历史，从发展的角度看，任何事物的存在都不是完备的，都有其一定的局限性，契氏公式也不例外。随着机构的发展、结构自由度研究的进展， 人们逐步揭示了机构学的运动本质和规律， 揭示了机构学与结构学之间的内在联系，自由度计算公式的局限性逐渐凸显出来。

1.1 仅适用于平面机构，不适用于空间机构。

一个活动杆件在平面上有三个自由度，一个平面低副引入两个约束，一个平面高副引入1个约束，故机构的自由度F=3n-2■-p■，显然契氏公式是适用于平面机构的。一个在空间不受任何约束而自由运动的构件共有六个自由度，每个运动副引入约束最多为五，最少为一，显然契氏公式不能满足分析空间机构的需要，基于此前苏联科学院通讯院士陀勃罗伏尔斯基于1943年提出空间机构自由度计算分式：

F=（6-m）n-■（i-m）p■ （2）

其中n为活动构件数， m 为机构各构件在运动时所受到的公共约束数， i 为i级运动副的约束数， 由运动副产生的约束数决定，P■为i级运动副的个数。

1.2不适用于全移动副平面机构。

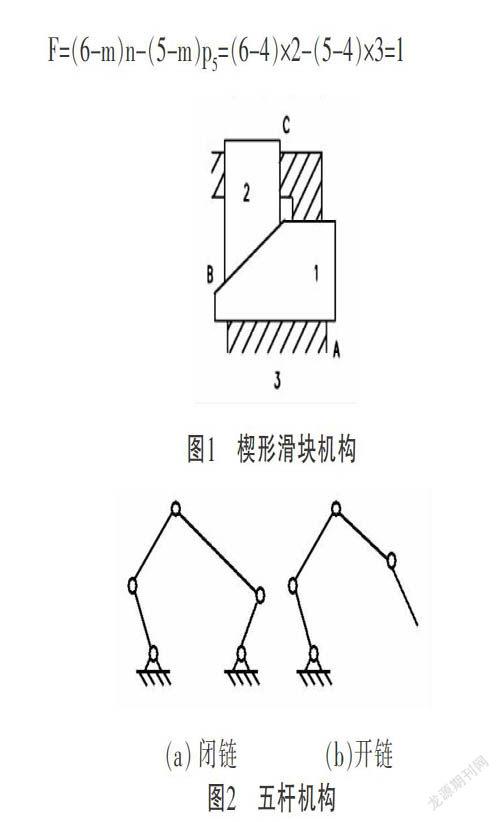
图1为平面楔形滑块机构，活动活动构件数n=2，低副数pL=3，高副数pH=0，计算得机构的自由度为F=0，这与实际情况不符。就一般推论而言， 平面机构可以理解为空间机构的特例，图1所示机构可以用上述空间机构自由度公式来计算。由于该机构为一全移动副平面机构，其两活动构件被限制在xy平面内移动，故其公共约束m=4，则该机构的自由度为：

F=（6-m）n-（5-m）p■=（6-4）×2-（5-4）×3=1

图1 楔形滑块机构

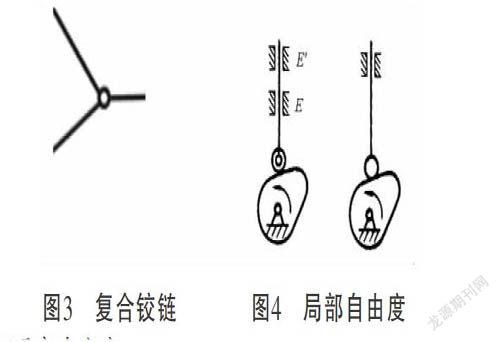
（a） 闭链 （b）开链

图2 五杆机构

1.3仅适用于闭链机构，不适用于开链机构。

图2为五杆机构，活动活动构件数n=4，图（a）中低副数p■=5，高副数p■=0，计算得机构的自由度为F=2，结果正确。图（b）中低副数p■=4，高副数p■=0，计算得机构的自由度为F=4，这与实际情况不符，由此看出契氏公式不适用于开链机构自由度的计算。

2.契氏公式应用时注意事项

契氏公式存在天然的缺陷与不足，然而时至今日，在我国的各种教材、设计手册中，契氏公式仍然还作为最主要的公式在使用，其在很多情况下计算是正确的，在计算机构的自由度时除了明确其使用条件外，还有一些应注意的事项必须正确处理，否则得不到正确结果。

2.1复合铰链。

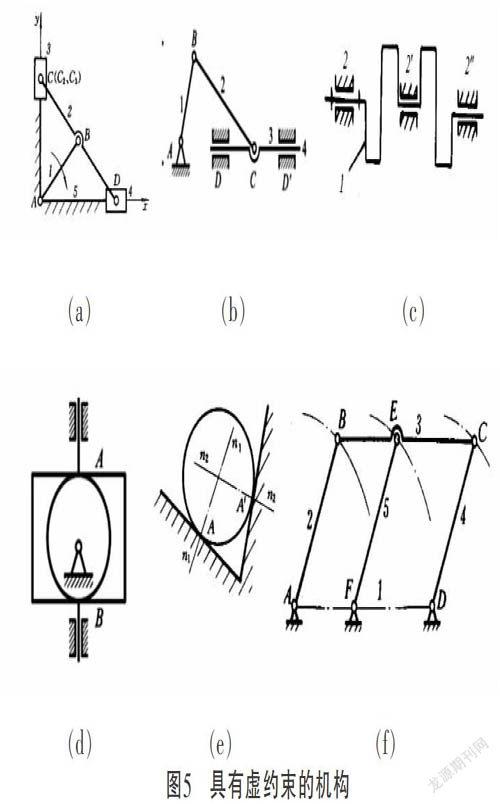
两个以上的构件同时在一处用转动副相连接就构成复合铰链。图3是三个构件汇交成的复合铰链，这三个构件共组成两个转动副。依次类推，K个构件汇交而成的复合铰链应具有（K-1）个转动副。在计算机构自由度时应注意识别复合铰链，以免把转动副的个数算错。

图3 复合铰链 图4 局部自由度

2.2局部自由度。

在有些机构中， 其某些构件所能产生的局部运动并不影响其他构件的运动， 我们把这些构件所能产生的这种局部运动的自由度称为局部自由度。如图 2 所示的凸轮机构，凸轮为主动件，顶杆为从动件。凸轮机构的功用是用顶杆获得预期的运动，滚子是为减少高副元素的磨损而加入的从动件，滚子与顶杆间形成的自由度不会影响输出件的运动，所以滚子与顶杆间的自由度为局部自由度，在计算机构自由度时， 假想滚子和安装滚子的构件固接为一个整体，成为一个构件或将机构中的局部自由度除去不计，否则机构的自由度为二，是不正确的。

2.3虚约束。

在机构中，有些运动副带入的约束对机构的运动只起重复约束作用，特把这类约束称为虚约束，在计算机构的自由度时应将这类虚约束除去，机构中的虚约束常发生在下列情况：

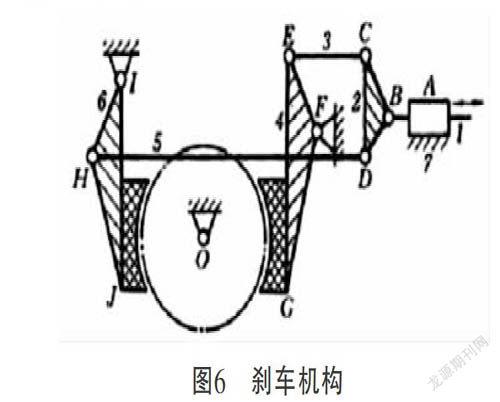
2.3.1在机构中如果两构件用转动副连接，连接前后其连接点的运动轨迹重合，则该连接将带入1个虚约束。如图5（a）中转动副C所连接的C■与C■两点的轨迹就是重合的，均沿y轴作直线运动，故带入一个虚约束。

2.3.2如果两构件在多处接触而构成移动副，且移动方向彼此平行，则只能算一个移动副。如图5（b）中构件3和4在两处形成移动副，且移动方向重合，则在计算自由度时只算一个；如果两构件在多处相配合而构成转动副，且转动轴线重合，则只能算一个转动副。如图5（c）中构件1和2在三处形成转动副，且转动轴线重合，则在计算自由度时只算一个；如果两构件在多处相接触而构成平面高副，且各接触点处的公法线彼此重合，则只能算一个平面高副，如图5（d）中两构件两处相接触而构成平面高副，且各接触点处的公法线彼此重合，因此只算一个高副。图5（e）中高副各接触点处的公法线不重合，所以此种情况没有虚约束。

2.3.3在机构运动的过程中，若两构件上某两点之间的距离始终保持不变，则如用双转动副杆将此两点相连，也将带入1个虚约束。图5（f）中连杆3作平动，BC线上各点的轨迹均为圆心在AD线上而半径等于AB的圆周。构件5与AB等长，两个转动副E、F对机构的运动不产生任何影响，由此带入1个虚约束。

应当注意，对于虚约束，从机构的运动观点看是多余的，但能增强机构的刚性，改善其受力状况，因而被广泛采用。但是虚约束的情况比较复杂，有时很难判断，因此分析时要注意机构的结构，具体问题具体分析，正确计算机构的自由度。

（a） （b） （c）

（d） （e） （f）

图5 具有虚约束的机构

3.机构自由度计算的思考

平面机构自由度的计算公式非常简单，但实际计算很复杂。对于一个工程实际问题，实际自由度的确定往往不能简单地套用公式计算，除了需要考虑复合铰链、局部自由度和虚约束等问题（特别是虚约束的问题，往往不容易判断）外，还必须具体问题具体分析。对此提出以下几点思考。

思考一：不管是最早的平面机构自由度公式，后来的空间机构自由度公式，还是现在的新公式[3]新方法[4]，机构自由度计算的思想是一致的。

一百多年以来，人们对机构的认识在不断提高，对机构理论的研究也越来越深入，机构自由度计算公式也在不断完善，无论公式的形式如何变化，理论如何更新，这些公式或方法的思想都是统一的，都是利用活动构件的自由度减去运动副引入的约束得到的。也就说只要正确获得活动构件的自由度与运动副引入的约束数，机构自由度的计算结果便是正确的。

思考二：活动构件数及自由度的判断是否正确，直接影响到机构自由度计算的正确性。

在现行各种教材及参考书中，都着重介绍复合铰链、局部自由度及虚约束等的分析判断，未见分析活动构件数及自由度对机构自由度的影响。实际上，对于全移动副楔形滑块机构自由度计算应用平面机构自由度公式是没错的，前提是搞清楚活动构件的自由度，如图1所示，活动构件数为2，移动副为3，由于两活动构件被限制在只能在xy平面内运动，即活动构件的自由度不再是3，而是2，移动副引入的约束不是2，而是1，则有F=2×2-3×1=1，结果正确。

在计算机构自由度时，活动构件数目判断不对，计算结果也是错误的。如图6刹车机构，若把车轮误认为机构的一个构件，则结果不正确。

图6 刹车机构

思考三：在分析运动副引入的约束时，应根据具体情况具体分析，不应一味照搬某些结论。一般认为平面机构中，转动副和移动副引入两个约束，但在图1所示楔形滑块机构中，移动副引入一个约束，这是因为两活动构件被限制在只能在xy平面内运动，单个活动构件的自由度为2，移动副只可能引入1个约束，若按引入两个约束计算，结果将是机构不能动，这与实际情况不符。

结语

机构理论不断发展，机构自由度公式也在不断完善，这些公式各有特点，在应用时除了要明确其适用范围，注意复合铰链、局部自由度及虚约束等问题外，对机构自由度计算提出几点思考，以便更好地运用和掌握公式，正确计算机构自由度。

参考文献：

[1]孙桓，陈作模，葛文杰.机械原理第七版[M].高等教育出版社，2006：13.

[2]张策.机械原理与机械设计（上册）[M].机械工业出版社，2011：28.

[3]欧阳富，蔡汉忠，廖明军. 机构结构新旧自由度计算公式对比之理论研究[J].中国机械工程，2010 .12，VOL21（24）.

[4]郭卫东，于靖军. 一种计算平面机构自由度的新方法[J].机械工程学报，2013.04，VOL49（7）.