高中立体几何二十四招式理论与实践（上）

薛超群

摘 要： 高中数学课程的总目标提出培养学生的空间想象等基本能力.如何在教学中对教材内容做进一步提炼、概括，总结立体几何招式套路在解决立体几何问题中的应用，将立体几何题目的解决转化为寻找相对应的招式，使学生学习起来能通俗易懂、快速有效.

关键词： 教材内容提炼 立体几何招式套路 解决立体几何问题

根据《全日制普通高中数学新课程标准》，高中数学课程的总目标是：使学生在九年义务教育数学课程的基础上，进一步提高作为未来公民所必要的数学素养，以满足个人发展与社会进步的需要.具体目标提出提高学生的空间想象等基本能力. 高中立体几何二十四招式理论，是将立体几何中最重要的解题思路总结归纳成招式模式，每一个招式指的是一种解题思路，共二十四个思路.高中立体几何二十四招式实践，是指高中立体几何二十四招式在解决立体几何问题中的应用，将立体几何题目的解决转化为寻找相对应的招式.高中立体几何二十四招式理论与实践，是指上述两项内容的总称.如何在教学中对教材内容做进一步提炼、概括，总结出立体几何招式套路在解决立体几何问题中的应用，将立体几何题目的解决转化为寻找相对应的招式，使学生学习起来通俗易懂、快速有效.

高中立体几何二十四招式前半部分简介如下：

招式一：看到中点找中点：看到三角形一条边的中点，取另一边的中点，连接两个中点.即若E为△ABC边AB中点，则连接E与另一边中点.

招式二：看到垂直做垂直：看到平面α⊥β，在平面α内作垂直于两平面交线l的直线α，则所作的直线l⊥β.即若α⊥β，α∩β=l，a∩α，a⊥l，则a⊥α.

招式三：看到等腰就劈断：看到等腰三角形ABC，连接顶点和底边中点.即若D为等腰三角形ABC底边BC的中点，则连接AD.

招式四：电线杆和田埂：直线l和平面α垂直，则直线l垂直于α内的任一直线a.即若l⊥α，a？奂α，则l⊥a.

招式五：泥工师傅灌平台：平面α内两交线分别平行于平面β，则α∥β.即若a？奂α、b？奂α，a∩b=O，a∥α，b∥β，则α∥β.

招式六：吊瓶架两垂直：直线l垂直于平面α内的两条交线，则l⊥α.即若a？奂α、b？奂α，a∩b=O，l⊥a，l⊥b，则l⊥α.

招式七：公理四传染病：直线a与直线b平行，直线b与直线c平行，则直线a与直线c平行.即若a//b，b//c，则a//b.

招式八：透过竹签就垂直：平面β经过另一个平面α的垂线l，则α⊥β.即若l⊥α，l？奂β，则α⊥β.

招式九：直躺二楼平一楼：平面α与平面β平行，直线l在平面α内，则l//β.即若l？奂α，α∥β，则l//β.

招式十：三推一：平面α外的一条直线a平行于平面α内的一条直线b，则a//β.即若a//b，a？埭α，b？奂β，则a//β.

招式十一：棱（人）无处不在：棱锥中，棱包括侧棱和底面多边形边长. 即在棱锥中，棱包括侧棱

招式十二：棱柱两平行：棱柱两个底面互相平行，侧棱也互相平行.即棱柱底面α与底面β互相平行，

利用以上的招式套路，可以解决大部分立体几何问题，思路清晰，简洁明快.

例1.如图，在正四面体A-BCD中，求证：CD⊥AB.

分析：要证明CD⊥AB，只需证明CD垂直于AB所在的平面.

看到CD=AC，BC=BD，用招式三“看到等腰就劈断”.

看到AD⊥AE，CD⊥BE，用招式六“吊瓶架两垂直”.看到CD平面ABE，用招式四“电线杆和田埂”.

证明：取CD边中点，连接AE、BE，

∵AD=AC，∴CD⊥AE，同理CD⊥BE，

∵AE∩BE=E，∴CD⊥平面ABE，

∵AB？奂平面ABE，∴CD⊥AB.

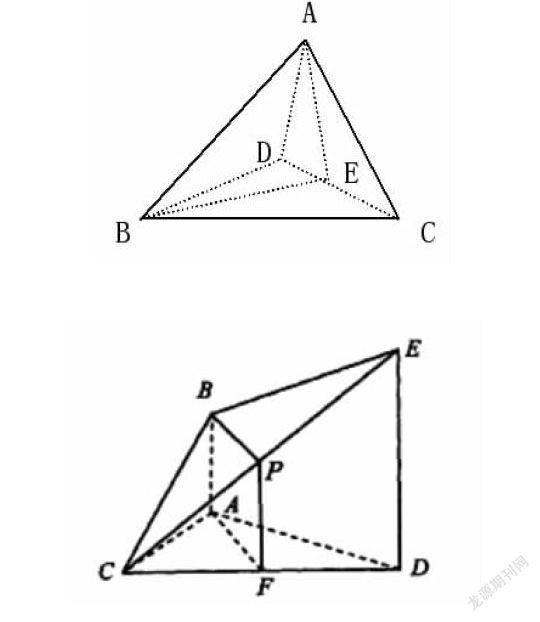
例2.如图，已知AB⊥平面ACD，DE//AB，AD=DE=2 AB，△ACD为正三角形，且F是边CD的中点.（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求证：平面BCE⊥平面CDE.

分析：（Ⅰ）要证明AF∥平面BCE，只需证明AF平行于平面BCE内的一条直线，用招式一“看到中点找中点”、 招式十“三推一”、招式七“公理四传染病”.

（Ⅱ）要证明平面BCE⊥平面CDE，只需证明平面BCE内的一条直线与平面CDE垂直，用招式一“看到中点找中点”、 招式十“三推一”、 招式七“公理四传染病”、 招式八“透过竹签就垂直”招式.

证明：（Ⅰ）取CE边中点P，连接连接BP、PF，

∵F是边CD的中点，∴PF//DE，∵DE//AB，∴AB//PF.

∵DE=2 AB，PF=2AB，∴AB=PF，∴四边形ABPF是平行四边形，

∴BP//AF，∵AF？埭平面BCE，BP？奂平面BCE，∴AF∥平面BCE.

（Ⅱ）由△ACD为正三角形，∴AF⊥CD，

∵AB⊥平面ACD，DE∥AB，∴DE⊥平面ACD，

∴DE⊥AF，CD∩DE=D，∴AF⊥平面CDE，

∵BP？奂平面BCE，∴平面BCE⊥平面CDE.

例3.如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2 AB=2 BC=2，O为AD中点.求证：PO⊥平面ABCD.

根据《全日制普通高中数学新课程标准》及心理学理论，在高中立体几何教学中，对有关概念、公理、性质等内容进行提炼总结，学生根据总结出的二十四招式套路，应用发现思维等寻找证明思路，可以提高立体几何解题能力，增强学习信心.

参考文献：

[1]全日制普通高中数学新课程标准.北京：北京师范大学出版社，2007.