探讨静力学中物体系统平衡问题的几种类型及求解方法
周佳园
摘 要: 正确求解物体系统的平衡问题,是工程力学的一项重要内容。本文对物体系统平衡问题的几种类型加以总结,并介绍相应求解方法。
关键词: 物体系统 平衡问题 求解方法
物体系统平衡问题相对于单个物体平衡问题要复杂一些,学生在求解物体系统平衡问题时,常常会感觉无从下手,不知道如何求解。对于物体系统平衡问题与单个物体平衡问题的区别在于研究对象的选择及解题的顺序。研究对象可以是整体,也可以取单个或一个部分的物体系统,解题顺序按照研究对象选择的顺序而定。本文把物体系统平衡问题分为几种类型,并为每种类型提供解题方法,只要分清属于哪种类型,并对症下药,问题便会迎刃而解。
类型一:以整体为研究对象未知力个数小于3个。如图1所示,该物体系统中,包含3个构件AB、ED、CD,以整体为研究对象,A处固定铰链2个约束反力,B处活动铰链1个约束反力,总共3个约束反力,受力图如图2所示,可以直接列3个平衡方程求解。如有需要还可以以个体为研究对象,约束反力小于等于3个,可以列平衡方程求解。
类型二:以整体为研究对象,未知力个数大于3个,以个体为研究对象未知力个数小于等于3个。如图3所示,物体系统包含AB、BC两个杆件,已知均布载荷q、集中力F,以整体为研究对象,A处固定端约束3个约束反力,C处活动铰链约束1个约束反力,未知力个数大于3个,此时以整体为研究对象列3个方程不能求解4个未知力。所以把个体拿出来画受力图分析,在求解时应该先取BC杆为研究对象,受力图如图4所示,因为BC杆上的未知力为3个,列平衡方程可以直接求解出来,而AB杆受力图如图5所示,未知力为5个,不能直接求解。以BC杆为研究对象,列平衡方程,求解出B、C处的约束反力,再以整体或者AB为研究对象就可以求出A两处的约束反力。
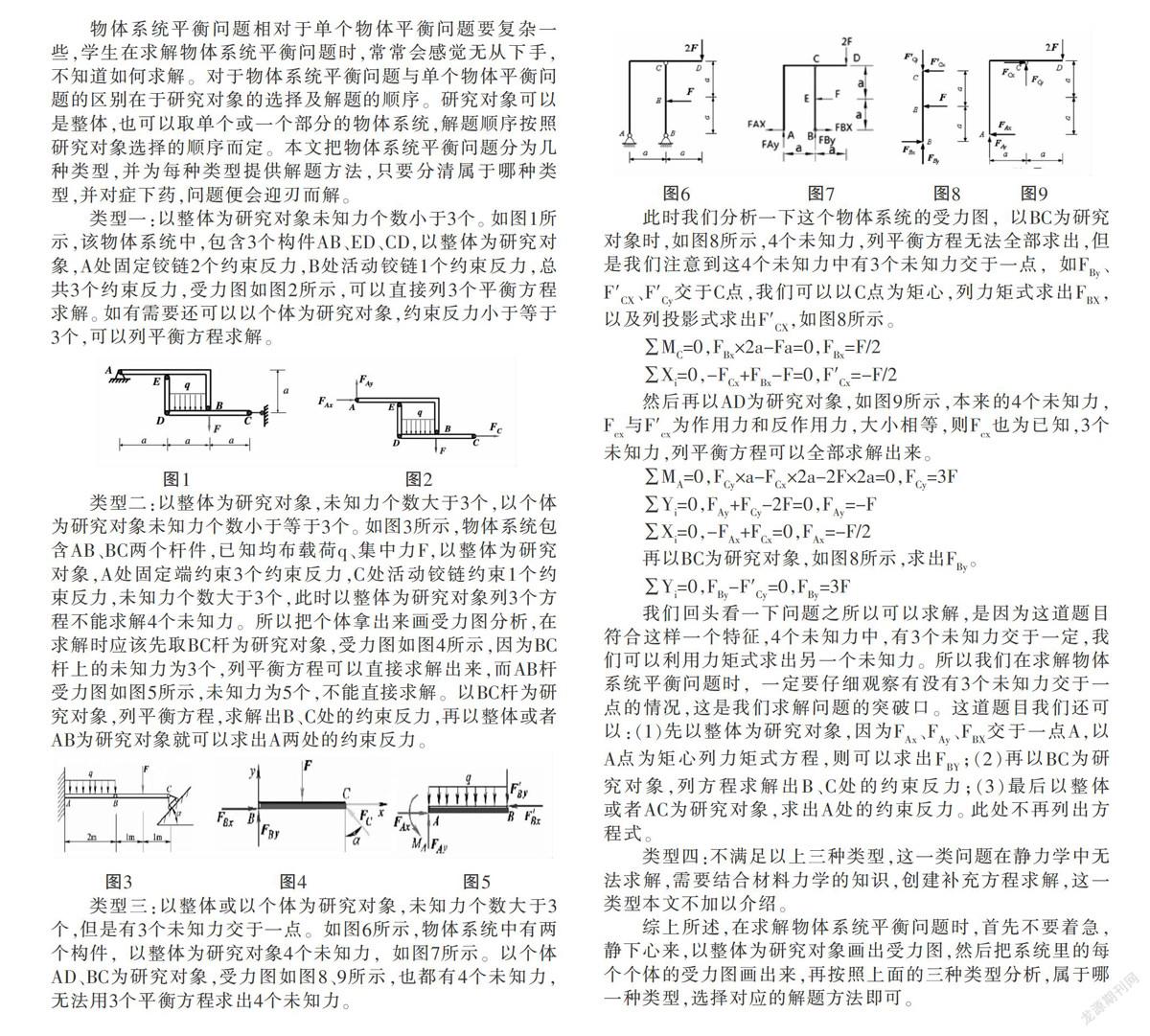
类型三:以整体或以个体为研究对象,未知力个数大于3个,但是有3个未知力交于一点。如图6所示,物体系统中有两个构件,以整体为研究对象4个未知力,如图7所示。以个体AD、BC为研究对象,受力图如图8、9所示,也都有4个未知力,无法用3个平衡方程求出4个未知力。
此时我们分析一下这个物体系统的受力图,以BC为研究对象时,如图8所示,4个未知力,列平衡方程无法全部求出,
我们回头看一下问题之所以可以求解,是因为这道题目符合这样一个特征,4个未知力中,有3个未知力交于一定,我们可以利用力矩式求出另一个未知力。所以我们在求解物体系统平衡问题时,一定要仔细观察有没有3个未知力交于一点的情况,这是我们求解问题的突破口。这道题目我们还可以:(1)先以整体为研究对象,因为F交于一点A,以A点为矩心列力矩式方程,则可以求出F;(2)再以BC为研究对象,列方程求解出B、C处的约束反力;(3)最后以整体或者AC为研究对象,求出A处的约束反力。此处不再列出方程式。
类型四:不满足以上三种类型,这一类问题在静力学中无法求解,需要结合材料力学的知识,创建补充方程求解,这一类型本文不加以介绍。
综上所述,在求解物体系统平衡问题时,首先不要着急,静下心来,以整体为研究对象画出受力图,然后把系统里的每个个体的受力图画出来,再按照上面的三种类型分析,属于哪一种类型,选择对应的解题方法即可。

