神圣的物理学球形牛

物理专业的很多学生在他们早年的学习中都会碰到球形牛这个概念。现实世界里的牛即使长得再壮或喂得再饱，也很难长成球形。这样一来，要想计算物体的体积或面积与其高度之比就是一个很麻烦的问题。但是，学生们了解到，如果假设牛为完美球体，或者说，牛具有球对称性，这些数字就很容易计算。强加某些潜在的（即使只是近似的）对称性，难题也能变简单。

球形牛的教学内容在本科阶段并没有学完，而是一直延伸到物理学的最前沿。在20世纪八九十年代，理论物理学界分裂为两派，起因就是对类似球形牛但比球形牛复杂得多的对称性是否具有现实性产生了分歧。弦理论家主张，用单一的数学描述对现实进行统一表达依赖于某些对称性，但几乎得不到实验支持;其他物理学家则认为，理论的角色是预测和解释实验，而不是追求自身的数学结构，不管这些结构有多美。对立双方在过去的10年中开始和解，他们意识到，弦理论家建立的有些精致工具，可以意想不到地用来解决其他问题，甚至有助于解释实测数据。

最简单的近似是两个电子通过交换一个光子而交互作用，近似计算的结果与实验结果颇为相符。而量子理论认为，电子可以来回传递任意数量的光子，如2个、3个，甚至900万个等。电子和光子之间有微弱的相互作用，因此，每种极其复杂的变异都应该对总振幅有一个适当的数值修正。问题是，即便是第二最简情形，即交换两个光子而非一个光子，计算起来已经极其困难。海森堡的一个学生非常勇敢，1936年尝试计算了一次，出版的公式就印了好几页。

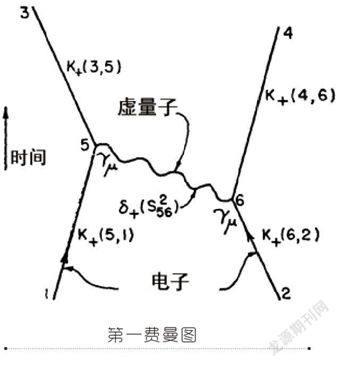
第二次世界大战后，一个名叫理查德·费曼的年轻人接受了这个挑战。他一边在纸上乱画，一边想象一系列事件（参见第一费曼图）。图左和图右两条线段代表电子在空间和时间的（向上）运动，通过释放和吸收一个光子来相互作用;光子携带的活力（能量和动量）足以改变每个电子的运动，因此两个电子向对方施加一个力，将各自推开。费曼用这个框架轻而易举地处理了两个电子之间更复杂的相互作用，将两个电子以各种方式往返交换两个光子的所有情形草草绘制出来。

2013年后半年，两位理论物理学家提出了一种被称为“幅面体”的新计算工具，这标志着物理学中的对称史翻开了新的一章。幅面体是一类古怪的几何多面体，处于多维抽象的学空间中，可以快速得出答案，而现在需要算几百张纸才能做到。最有意思的是，它的力不只是凸显一些对称性，也在于舍弃旧的对称性。这样一来，就可以指出一条道路，改变我们思考空间和时间的方式。

图解寓言

20世纪20年代后期，量子理论的伟大缔造者维尔纳·海森堡、沃尔夫冈·泡利和保罗·狄拉克等人认识到，物理的力是通过交换某些载力的粒子产生的。例如，光子（单个光粒子）就是电磁的载力粒子，电子等带电粒子相互间通过往返传递光子施加电磁力。经过20世纪30年代的发展，物理学家已经想出办法来粗略计算这类过程的“振幅”，由此知道这些过程发生的概率。

费曼图成了寓言，每个要素都传递一定的信息。一个电子有发射或吸收一个光子的一定概率，正如一个光子有从点A到点B畅通无阻地移动的一定概率一样。费曼为其图中的每一种要素找到了对应的数学表达式。手中有了这些简单的转化规则，他用30分钟就解决了困扰世界上顶级理论物理学家几十年的计算问题。

从此以后，物理学家用费曼图完成了更为复杂的计算。例如，康奈尔大学的木下东一郎就率先对电子间交换4个光子的结果进行了计算，涉及近900个不同的费曼图，其理论结果与实验测量的误差小于一万亿分之一，是迄今科学史上理论和实测最接近的结果。

对称性与神来之笔

费曼发明他的图是为了方便计算电子和光子间的交互作用。在他引用这张图之后不久，物理学家就把它运用于一组相当不同的交互作用：核力。这种转变并不总是一帆风顺的。一方面，核粒子相互之间的作用力很强，不像电子和光子之间的作用那么微弱。这就意味着需要更复杂的图，在交互中需要更多的载力粒子，不能再对简略图示做些微修正。这些更为复杂的图在计算振幅时应当比简图的权重更大，这就需要考虑无限多的图。费曼开始产生怀疑，他于1951年晚些时候在写给恩里克·费米的信中说：“介子理论如果使用了费曼图，所做的计算不要相信！”

虽然费曼心有疑虑，但其他人仍然在继续努力。在最早采用费曼图的学者中，有当时在纽约长岛新建的布鲁克海文国家实验室工作的年轻理论家杨振宁和罗伯特·米尔斯。布鲁克海文国家实验室拥有当时功率最高的粒子加速器之一，而杨振宁和米尔斯也正迫切地想弄明白，加速器揭示的核粒子种类和相互作用为什么花样多得令人头晕目眩。

1954年，杨振宁和米尔斯重新捡起海森堡在20世纪30年代早期曾经徘徊过的想法：在考虑核作用时，中子和质子似乎无法分辨。它们当然是不同的粒子：质子带有一个单位的电荷，而中子不带电。然而，中子和质子似乎以对称的方式与π介子等其他核粒子相互作用。质子交换中子或者用中子交换质子，似乎根本没有太大的影响。物理学家把这种无关紧要的差异称为“规范不变性”。

两位年轻的物理学家将这种隐隐约约的对称性提升为一种创造性原理，建立了一个新的核力模型。如果所有的核作用力都必须遵守中子和质子间的对称性，那会怎么样？他们发现，只有引入一种新的粒子，这种对称性才能产生。这种假设的规范粒子的唯一目的（至少杨振宁和米尔斯的计算是这样的），就是以某种方式撞开其他核粒子，在涉及质子对中子的计算结果中抵消任何可能的偏差。同时，这种散射意味着规范粒子会传递力，它是核力的载力粒子，是电磁作用中光子的“表亲”。

这是携带着复仇的对称。杨振宁和米尔斯从海森堡的直觉和散射实验证据中实现了一次大的跳跃，认为中子和质子是精确对称的。为了保护这种对称，他们只能设想一种全新的物质，这正好产生了杨振宁和米尔斯一开始就想理解的核粒子之间的作用力。

20世纪70年代中期，粒子物理学家拼接出一个复杂的核力理论，称其为“标准模型”，其中包含几种不同的规范粒子。数年之内，他们开始积累胶子的实验证据（胶子是将夸克束缚于质子、中子和其他核粒子之内的规范粒子）。1983年，欧洲核子研究所庞大的实验队伍首先探测到了弱核力（引起核衰变的核力）的规范粒子。曾一度被认为只不过是数学工具的杨—米尔斯规范粒子从此成为我们世界的一部分，也成为潜在对称性的物理实例。

确定了规范粒子的真实性之后，物理学家需要计算它们的行为，包括具体的散射振幅。实现这一步很艰难。杨振宁和米尔斯对费曼的图式计算规则做了适度的改动，为保证规范对称的要求允许规范粒子间直接散射。这看上去简单，但实际做起来实在颇费脑筋。现在需要将规范粒子形成的闭环加入费曼图，这种复杂的情况在电子和光子相互作用的图中不可能出现。

1963年，费曼证明这种闭环会破坏引入规范粒子所强加的对称性。所以，物理学家只得在计算中添加更多奇怪的数学运算，包括虚构的“鬼”粒子。这些粒子的唯一目的，就是在某些特定类型的费曼图中跟在规范粒子周围，最终在把费曼图加到一起的计算中相互抵消。“鬼”粒子和规范粒子不同，它是数学上的虚构，并不代表真实粒子，有了它就可以将费曼图应用到杨—米尔斯对称模型。

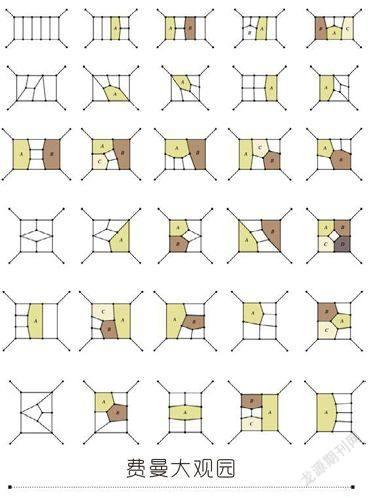
结果，在过去的几十年里，物理学家用这种变通的办法，在黑板和杂志上画满数以百计带着各种规范粒子和“鬼”粒子的费曼图，全力应对这一事实：杨振宁和米尔斯引入的对称性似乎把计算搞得一团糟（见费曼大观园）。

于是，他们引入另一种被称为“超对称”的对称性，作为一招缓兵之计。乍一听超对称有点古怪：先准备两份所有已知种类的物质，这样一来每个粒子就有了一个几乎与自己完全相同的“超伴子”，唯一不同的是它们携带的内禀角动量（或称“自旋”）。所有这些成对的粒子在所有费曼图中精确抵消，极大地降低了既定计算的复杂性。

然而，即使有了超对称，任何涉及夸克和胶子的散射振幅的计算还是会让物理学家陷入笨拙庞杂的图式计算的泥淖。按照唐纳德·拉姆斯菲尔德的说法，费曼图里至少描绘了三类野兽：有已知的已知者，比如夸克和胶子等确实存在于我们世界中的粒子;还有已知的未知者，比如只存在于物理学家想象中的“鬼”粒子，不代表现实世界中的任何实物;然后就是那些超伴子，也就是未知的未知者。

几十年的协作搜寻，甚至动用了欧洲核子研究所的大型强子对撞机，竟然还是没有发现超伴子粒子存在的实验证据。不过，拉姆斯菲尔德曾经很有底气地声明：没有证据并不一定是没有证据。我们的宇宙也许确实是由超对称主宰的，而且所有超伴子总有一天会被发现。但是，它们也可能只是方便的数学假设，是“鬼”粒子的加强版。现在看上去清楚的是，超对称仍然很方便，我们还舍不得抛弃：它是受喜爱的微观世界球形牛。

新任务的新工具

尼玛·阿卡尼·哈米德是普林斯顿高等研究所的一名教授，也是论文被引用次数最多的物理学家之一。尽管他现在才40多岁，但他的论文被引用数已经是理查德·费曼生前所有论文被引用总数的2倍。现在，阿卡尼·哈米德和他以前的学生（也是论文的共同作者）雅罗斯拉夫·特恩卡一起，向每个物理学家计算粒子相互作用时都会碰到的巴洛克艺术般庞杂的计算发起了攻击。

2013年12月6日，阿卡尼·哈米德和特恩卡在arXiv预印本服务器上传了一份讨论幅面体的论文，观点很大胆。文中说，他们为费曼图找到了一个替换，至少可以用来处理载力粒子间直接散射的相互作用（比如说核力）。在超对称模型内进行对比，新的方法能够用数行代数式复制其他人绞尽脑汁计算几百（甚至几千）个费曼图才能得到的散射振幅。

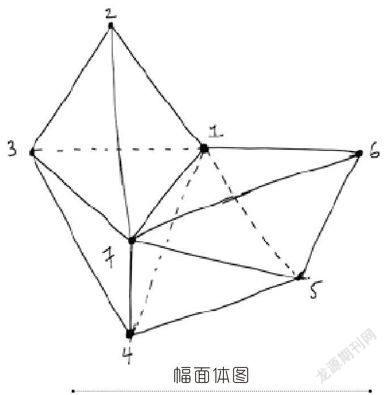
阿卡尼·哈米德和特恩卡用他们精致简约的几何构型幅面体展示了这种新的计算方法。和费曼的涂鸦不同，他们不在空间和时间内描绘，而是处于一种想象的多维数学空间。图中的锚点代表粒子动量、自旋和其他变量的坐标，并不是它们在空间中相遇时的位置。

任何散射下，总动量和总自旋都必须守恒。因此，每个幅面体都是由封闭的多边形构成的，从本质上说，就是由简单的三角形构成。阿卡尼·哈米德和特恩卡像玩魔术一样向我们证明（至少在几个实例中），通过计算相应幅面体的体积，他们得到了和旧方法相同的各种粒子的散射振幅，但不需要那些充满了闭环和“鬼”粒子的费曼图。

结果省时省力，令人激动不已。牛津大学的安德鲁·霍奇斯和哈佛大学的雅各布·布杰利等物理学家，对幅面体方法异乎寻常的浓缩和简约惊叹不已。布杰利说：“这种有效程度令人难以置信。”这是66年前物理学家目睹理查德·费曼用他的图首次计算时的反应的再现。

幅面体的威力在于将一种对称性置于另一种对称性之上。它凸显的那种对称性就是振幅本身，而振幅则由动量守恒等最基本的原理限制。交换一个向外的粒子与一个向内的粒子相当于旋转幅面体，有些旋转可以保持幅面体不变，就像一个十二面体沿一个轴旋转特定角度后看上去完全没有变化一样。对阿卡尼·哈米德和特恩卡来说，这种整体对称性（使整个幅面体结构保持不变的旋转操作）比局部的规范对称性更重要。

也就是说，他们抛开了某些局部的对称性。事实上，他们抛开（或者至少未看重）的正是“局域性”这个概念本身。费曼在设计他的图时假设，当一小块物质在地点X和时刻t与另一小块物质相撞，由此发生的所有物理效应都是局部的。费曼并不需要知道每个碰撞发生的精确位置——他在计算振幅时会对所有位置做积分，但他还是假设每个碰撞都发生在时间和空间中的某个局部位置。

而阿卡尼·哈米德对局域性有不同的看法。在他看来，终极奖品是量子引力理论，幅面体只不过是一座营帐。因为量子引力理论可能会从更深的层次和结构解释空间和时间的出现，他渴望规避对局域性的任何假设，因为局域性的概念已经预先假定了空间和时间的存在。尽管幅面体没有假定局域性，但它产生的结果遵守局域性：局域性是阿卡尼·哈米德理论框架的发生特征，而不是起始假设。

未来

我可以想象一个分形图案在眼前展开。在将来的某一天，我们能够看见幅面体铺满了年轻物理学家的黑板（或平板电脑），使他们觉得需要再发明另一种工具来表示数以百计的幅面体计算，就像一个幅面体能表示几百个费曼图，一个费曼图能表示十几行代数运算那样。每一代人都要重新评估前辈认为理所当然的对称性。一位物理学家神圣的球形牛在另一位物理学家看来，是一种低效率的处理方案。

不过，幅面体及其依赖的超对称仍然是未经证明的猜想。我们知道的是，如果避开局域对称性而强制整体对称性，幅面体就能让物理学家相当轻松地计算复杂的相互作用。即使将来证明了超对称并不是对我们宇宙的精确描述，幅面体的成功也能表明，自然最基本的力也许受到一个比费曼图展现出来的结构更深层、更简单的数学结构的支配。

就这一点来看，幅面体方法让旧的费曼图如同20世纪40年代后期那种塞满房间、密集组建的真空管计算机一样过时了。幅面体究竟是准确的，还是比较好的对称性近似（最新的球形牛），物理学家会在未来几年内搞清楚。他们仍将苦苦思索：应该采用哪些对称性，如何采用这些对称性。

大卫·凯撒，麻省理工学院科学、技术及社会项目的项目主任，麻省理工学院物理系高级讲师。