几类特殊图的拉普拉斯Estrada指标估计
蔡素丽
(福州外语外贸学院)
1 基本概念
在该文中,仅考虑无圈,无重边的无向简单图.
设G=(V,E)是n阶简单图.其顶点集和边集分别记为V=V(G)={v1,v2,…,vn}和E=E(G)={e1,e2,…,en},dG(vi)表示顶点vi在图G中的度且满足M(G)+2m,λ1,λ2,…,λn为图G的邻接矩阵A(G)的特征值,也称为图G的谱.设λ1≥λ2≥…≥λn.图G的谱满足下面的等式关系:
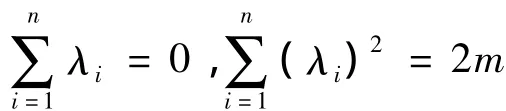
矩阵L(G)称为图G的Laplacian矩阵.设μ1≥μ2≥…≥μn=0为L(G)的特征值,也称为图G的Laplacian谱.
图的Estrada指标定义如下:

定义1.1[1]设G是一个(n,m)-graph,且其Laplacian特征值为μ1≥μ2≥…≥μn=0,那么G的Laplacian Estrada指标定义如下:

定义1.2[2]设G是一个(n,m)-graph,且其Laplacian特征值是μ1≥μ2≥…≥μn=0,图G的Laplacian Estrada指标定义为:

2 主要结论
2.1 关于格子图的L-Estrada指标问题
定义2.1.1[3]平面格子图Pm×Pn的定义为:

引理2.1.1m阶的路Pm的Laplacian谱为

引理 2.1.2[4]设λi(G1),λj(G2)分别为图G1和G2的 Laplacian特征根,则G1×G2的Laplacian特征根为λi(G1)+λj(G2)i=1,…,|V(G1)|,j=1,…,|V(G2)|
定理2.1.1m×n阶格子图Pm×Pn的Laplacian谱为:

定理 2.1.2- 26.799075+16.843984m.
证明 由引理2.1.1知阶为m的路Pm的Laplacian谱为m–1.
根据定义1.1、引理2.1.1 可得LEE(Pm)=
通过Excel散点观察(图略)知路Pm的拉普拉斯Extrada指标与阶数m呈线性关系,设拟合方程为LEE=am+b,运用最小二乘法作线性拟合.
可得LEE(Pm)16.843984m.
定理 2.1.3LEE(Pm×Pn)=LEE(Pm)·LEE(Pn)≈ 283.719786mn– 451.403184(m+n)+718.190427.
证明 根据定义 2.1.1、定理 2.1.1,定理2.1.2 可得:
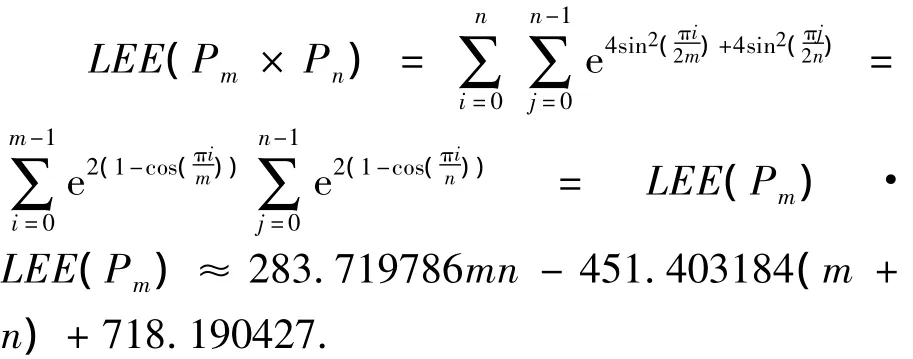
2.2 关于轮图的L-Estrada指标问题
用积分逼近方法得到轮图的L-Estrada指标近似表达式.
定义2.2.1 图G和H的联图G∨H定义为:
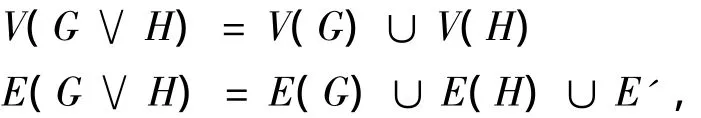
其中E'={gihj|i=1,2,…,p;j=1,2,…,q}.
定理2.2.1[5]设|G|=p和|H|=q且图G和H的Laplacian谱分别为:

则有联图G∨H的Laplacian谱为:
引理2.2.1n阶轮图Wn的Laplacian谱为

定理 2.2.2LEE'(Wn)

证明 因为Wn=Cn-1∨K1,所以E(Wn)=2(n– 1).根据定义1.2、引理2.2.1 可得:

当i=1,2,…,n–1时,角2iπ/n均匀地分布在区间[0,2π]中,当n充分大时,得到近似表达式:
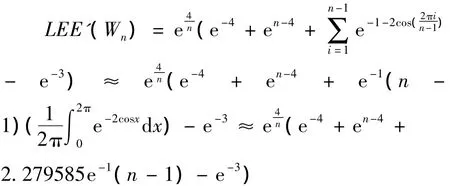
证毕.
2.3 关于单点粘合图的L-Estrada指标问题
定义2.3.1 设G1是(n1,m1)-graph,G2是(n2,m2)-graph,vi、uj分别是G1和G2的任意两个顶点,G1和G2的单点粘合G1⊙G2是(n1+n2-1,m1+m2)-graph,即为将G1∪G2中点v1与uj粘合所得到的图.
引理2.3.1 设G为(n,m)-graph,且它的顶点的最大度为Δ,最小度为δ,那么

等式成立当且仅当G是正则图.
引理2.3.2 设G1,G2是两个图,阶数分别为n1,n2,图G1⊙G2是G1和G2的单点粘合图,记μ1(G1)≥μ2(G1)≥…≥μn1(G1)=0,μ1(G2)≥μ2(G2)≥ … ≥μn2(G2)=0,μ1(G1⊙G2)≥μ2(G1⊙G1)≥ … ≥μn1+n2(G1⊙G2)=0,那么

定理2.3.1 设G为(n,m)-graph,且它的顶点的最大度为Δ,最小度为δ,那么:
LEE(G·G)≤2(n–1)+4m+e2M(G)+2Δ2+4m–

证明 对整数k≥3,

定理2.3.2 设G为(n,m)-graph,且它的顶点的最大度为Δ,最小度为δ,那么:

当且仅当G=ˉKn时,等式成立.
证明 假设n≥1,对非负实数a1,a2,…,ap且l≤k,l,k≠ 0,有不等式:

当且仅当a1=a2=…=ap时,等式成立.那么对
k≥2,p=n,l=2且ai=μi(i=1,2,…,n),有:


定理2.3.3 设G是一个r正则图,顶点数为n,那么:
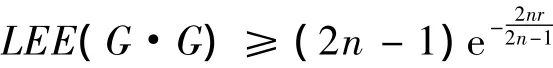
证明 如果图G是r-正则图,由引理3.1.1有μi(G)-r=–λn-i+1(G),i=1,2,…,n.其中λ1=r,λ2,…,λn是图G的一般特征值,它们按递减的顺序排列.通过使用算术几何不等式,我们得到:

证毕.
以上给出了关于格子图、轮图的拉普拉斯Estrada指标的近似计算公式以及单点粘合图上界和下界.该文还有待改进,如该文只对相同图的单点粘合拉普拉斯Estrada指标进行估计,有待进一步改进为任意图形单点粘合的情况.
[1]Zhou B,Gutman I.More on the Laplacian Estrada index[J].Appl Anal Discrete Math,2009(3):371-378.
[2]Li Jianxi,Wai Chee Shiu,Chang An.On the laplacian estrada index of a graph[J].Appl Anal Diacrete Math,2009(3):147-156.
[3]Noman Biggs Algebraic Graph Theory[M].2nd ed London:Cambridge Vniversity Press,1974.
[4]Fiedler M.Algebraic connectivity of graphs[J].Czech Math,1973,23(98):298–305.
[5]Cvetkovi D,Doob M,Sachs H.Spectra of Graphs-Theory and Application[M].Berlin,Heidelberg,1995.

