深水多波束测深系统海底回波信号快速仿真方法

张威，刘晓东，刘治宇，刘小刚，董飞



深水多波束测深系统海底回波信号快速仿真方法

张威1,2，刘晓东1,3，刘治宇1,3，刘小刚1，董飞1

(1. 中国科学院声学研究所海洋技术实验室，北京100190；2. 中国科学院大学，北京1000190； 3. 中国科学院声学研究所声场声信息国家重点实验室，北京 100190)

针对传统深水多波束测深系统海底回波信号仿真方法计算量大和不适用于存在载体姿态的问题，提出一种深水多波束测深系统海底回波信号快速仿真方法。基于扩展散射体海底回波信号仿真模型，考虑载体姿态，通过预先计算海底散射点强度分布确定主要作用区域的散射点，并将这些散射点的强度作为回波信号幅值加权来得到回波信号。利用这一方法，在保持较小计算量的同时，可以得到包括载体姿态特征的仿真数据。此外，利用这种方法还可以进行相位不一致性等误差因素的仿真。

深水多波束；海底回波仿真；载体姿态

0 引言

海底回波信号仿真在声呐制造以及信号处理相关研究领域有着重要的作用。近年来，国内外学者提出了诸多的仿真模型，主要可以分为两类：声线模型和声管模型。声线模型是根据光学中的光线跟踪技术发展而来，可以很好地反映海底的统计特性[1]。2007年Didier Gueriot等人在声线跟踪技术的基础之上提出了声管跟踪技术[2,3]，可以有效仿真背向散射强度。综合这两者的特点，Yoann Ladroit等人提出了扩展散射体模型[4]，既可以反映出海底的统计特性也可以反映出背向散射强度，该模型非常适合于开展浅水多波束测深系统等信号的仿真。

但是对于深水多波束测深系统[5]，利用这些模型所需的计算量非常大，很难在合理时间内实现。其原因在于，深水多波束测深系统探测海域最深11000 m，覆盖可达几十公里，信号长度长，典型发射基元可达近千个，接收基元可达一百多个，因此需要采取一定的策略，在不显著影响精度条件下降低模型的运算量。

此外，现在主流深水多波束测深系统都采用波束稳定技术，即根据当前船舶姿态确定波束形成方向并判别海底位置，为验证这些信号处理算法，需要对载体存在姿态条件下对海底回波信号进行仿真，这需要对上述海底方案模型进行改进。

为此，在扩展散射体模型的基础上，本文提出一种利用散射点强度分布选出起作用的散射点的选取方案来加快仿真计算速度，同时将散射点强度值为回波信号幅值加权来反映姿态变化，使得仿真模型在保持较小计算量的同时适用于存在载体姿态条件下的回波信号仿真。

1 扩展散射体模型

1.1 模型简介

首先简要介绍Yoann Ladroit等人提出的扩展散射体模型[4]。声呐系统的海底回波信号仿真基本过程如图1所示，从发射端开始，通过控制各个发射基元时延来控制发射波束指向性，发射信号经过海底各个散射点产生背向散射信号，回波信号被接收基元所接收。

扩展散射体模型中通过选定一定波束宽度覆盖的海底区域，网格化为散射单元，散射单元有面积特征量，从而使得回波信号中既可以反映出海底统计特性，又可以反映出背向散射强度特征。回波信号表达式为

1.2 存在载体姿态下的解决方案

虽然此模型在回波信号反映的信息量上有所改进，但若要对存在载体变化时的海底回波信号仿真，载体姿态会引起发射基元位置的变化，在做波束稳定时，每一个发射基元需要补偿的时延不同，需要针对每个发射基元，计算各个散射单元对该基元发射信号的回波信号到各个接收基元的信号(图2)，这样才可以对载体姿态引起的时延对各个发射通道进行补偿，从而反映出载体姿态信息和发射基元相位不一致性等特性，其回波信号表达式为

其中，M为发射基元个数，其计算量与深度的三次方和基元数的一次方成正比。对于深水多波束测深系统，基元个数多(几百个)，发射波束数量多，仿真计算量将非常大，例如对于5000 m水深的条件下，普通PC需要几天的时间。为此，提出了一种改进方法，称之为基于幅值加权的仿真算法。

2 基于幅值加权的仿真算法

算法的基本思想是：

(1) 根据信号类型和载体姿态估算覆盖范围并网格化，计算各个散射点到各个发射基元的时延从而得到各个散射点上的强度分布；

(2) 根据散射点强度分布选取一定强度值内的散射点；

(3) 将起作用的散射点的强度值归一化后作为回波信号幅值的加权值。扫描每个采样时刻起作用的散射点，此时起作用的散射点的回波信号的叠加即为此采样时刻的信号。

下面给出每个步骤的具体算法。

2.1 波束脚印

海底散射点强度分布可以反映出发射波束在载体姿态影响下的变化，载体姿态有三个方向的变化：艏摇(yaw)、纵倾(pitch)、横滚(roll)，用表示偏航角，表示在水平面内船头方向偏离航迹方向的角度，定义从船上方看去，船头顺时针偏离航迹方向为正，反之为负；用表示纵倾，表示船头方向与水平面的夹角，且定义船头抬起为正，反之为负；表示横滚，定义左舷抬起为正，反之为负。当载体存在姿态变化时，换能器基元坐标可通过公式(3)[6]换为有姿态变化后的坐标：

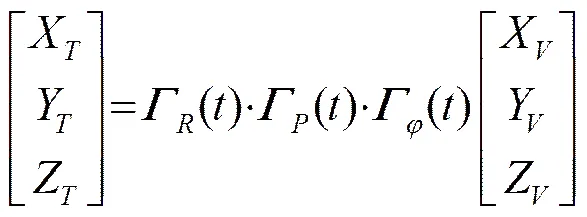
为达到较好的描述效果，仿真过程中使用了发射三维波束稳定算法，该算法的基本思想是通过实时计算载体姿态引起的时延，对各个发射通道进行时延补偿，从而将发射波束主轴稳定在相对于发射中心的固定方向。图3给出了在500 m水深、三种姿态共同作用下海底散射点强度值分布图，可以看出，利用所有发射基元计算出的散射点的强度值分布可以有效反映载体姿态变化对发射波束的影响。因此，可以通过将海底各个散射点的强度作为加权值加入仿真信号中，从而使回波信号中含有载体姿态信息。

2.2 海底散射点划分

深水多波束测深系统一般采取多个发射波束的方案，因此如果按照现有的选取方法会造成选取范围过广的问题。现有仿真模型中散射点的选取一般采用将海底曲面进行网格化的方法，每一个小网格作为一个散射单元，每个发射波束散射单元覆盖的范围可以由公式(5)估算出。

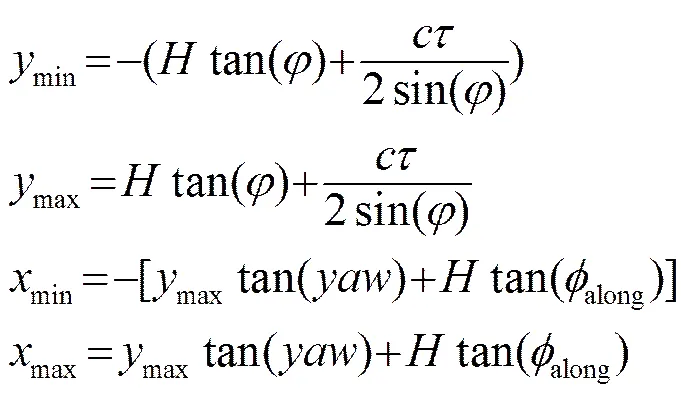
定义这种散射点选取方法为矩形区域选取方法，然而，这样所得的覆盖区域中，有很大一部分的散射点在波束指向性的影响下对波束信号贡献很小。因此，可以根据散射点强度分布选取其中主要起作用的点来进行信号的仿真，以达到尽量降低散射点数的目的。图4中给出了5°条件下矩形区域选取方法与本文散射点覆盖区域的对比，图中填充部分为-3 dB波束覆盖范围，可以满足垂直于航迹方向±65°的覆盖，同时散射点的数量较之矩形区域要减少很多。实际仿真时可以根据声呐系统的波束宽度和频率对强度范围进行调整。

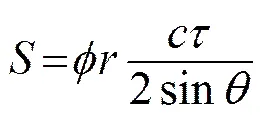
2.3 海底回波信号模型

回波信号模型如图6所示，为发射源，当做点源；为接收源，接收端需要将各个接收通道的信号进行仿真，用于波束形成；为散射单元面的法向量；为第个散射单元的入射信号；为第个散射单元的回波信号。在不考虑噪声、混响等干扰因素的情况下，回波信号可用公式(7)表示：

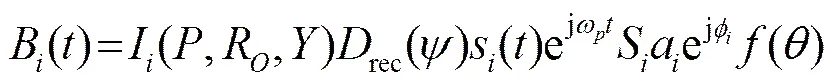
其中：表示与载体姿态有关的散射点强度；Y表示偏航角；P表示纵倾；表示横滚；为散射单元面积；假设各个散射单元的振幅为瑞利分布；为接收基元沿着航迹方向波束指向性，相位均匀分布在；表示背向散射模型，可以根据需要选择不同的背向散射模型，本文采用Lambert模型：。

3 仿真算法性能分析

利用第2节中的回波信号仿真方法，本文以国产深水多波束测深系统为参数模型，对海底回波信号进行了仿真。发射阵列和接收阵列如图7所示，发射阵错开排列方式与间隔半波长整齐排列平面阵相比，增大了发射阵垂直于龙骨方向的孔径，增强首摇的姿态稳定能力，在船舶姿态变化较大时仍能实现测量的宽度覆盖技术。在加入载体姿态条件下，从回波信号的相位差曲线、测底结果、计算复杂度、计算速度和仿真误差上与扩展散射体仿真方法进行对比。

浅水仿真条件：

(1) 水深：500 m

(2) 发射方向：[-50°, 0°, 50°]

(3) 发射频率：12 kHz

(4) 发射阵：72×12交错排列阵，浅水区域可以只采用72×2交错排列阵

(5) 接收阵：1×64线阵

(6) 脉冲长度：2 ms

(7) 信号类型：CW信号

(8) 载体姿态：roll=pitch=yaw=5°

3.1 平坦海底仿真结果

海底回波仿真信号后处理均采用实际海试数据后处理程序进行处理，正下方区域采用幅值法，边缘区域采用相位法[8]。图8、9给出了不同接收方向幅值和相位差变化，正下方±10°以内相位差模糊，其他方向相位差变化平滑，与理论相符。

图10、11给出了不同仿真算法的海底回波仿真信号左右舷边缘接收波束的相位差曲线对比。可以看出，在同等散射点密度的条件下，本文提出的基于幅值加权模型的相位差曲线与扩展散射体仿真方法的相位差曲线基本一致，虽然相位差曲线有轻微抖动，但是经过拟合后可以得到较为准确的回波时延。

为减小载体姿态对测深结果的误差，对结果使用了归位算法[6]，测底结果如图12、13所示。本文提出的基于幅值加权模型的深度结果与扩展散射体仿真方法的深度结果基本一致，其中边缘结果一致性良好，正下方附近深度误差略大，但在仿真允许的范围之内。

表1给出了不同仿真算法在载体姿态时不同发射波束测底相对误差的中值对比，两种仿真算法都具有较小的误差。

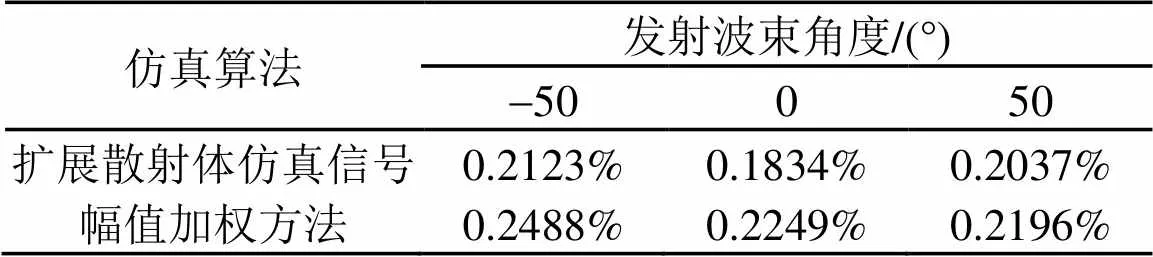
表1 仿真信号测底相对误差中值

3.2 非平坦海底仿真结果

实际海底地形是变化多样的，最常见的海底地形是斜坡，无论是剧烈变化的斜坡(悬崖)还是坡度，都是常见的海底地形。本文针对V型斜坡海底进行了仿真。仿真条件与前面相同，姿态为roll=pitch= yaw=5°。从测底图(图14)中可以看出，对于斜坡海底，本文的海底回波信号仿真方法仍然保持着较小的误差。

3.3 计算量分析

本文提出的仿真算法中，发射端当做点源，根据散射点强度分布，只选择-3 dB范围以内的散射点。计算散射点强度的计算量与生成海底回波仿真数据计算量相比可忽略，因此，幅值加权的仿真方法的计算复杂度为：

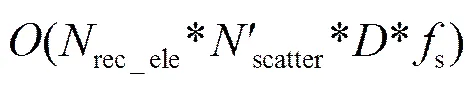
扩展散射体仿真模型中将各个发射基元信号都进行仿真，该方法最贴近实际信号产生过程，但是计算复杂度过高，其计算复杂度为：

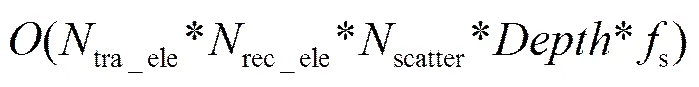
从理论上讲，添加姿态的扩展散射体仿真模型与本文提出的基于幅值加权的仿真方法都是利用各个散射点背向散射信号的叠加进行计算。本文的仿真算法在减小计算量的同时也适用于具有载体姿态条件下的回波信号仿真，在把发射端当做点源的情况下可对姿态、相位不一致性情况进行仿真。

表2给出了在普通计算机Matlab平台上仿真时间随海底深度的变化，具体仿真参数与前面相同，本文提出的仿真算法在保证信号真实性的同时计算速度最快。在用于多发射基元的声呐系统海底信号仿真时，计算速度可以有着显著的提高。

以上分析可以看出，本文提出的仿真模型，对于不同姿态条件下所仿真的信号较好地反映了海底地形，并且具有计算量小的优点。

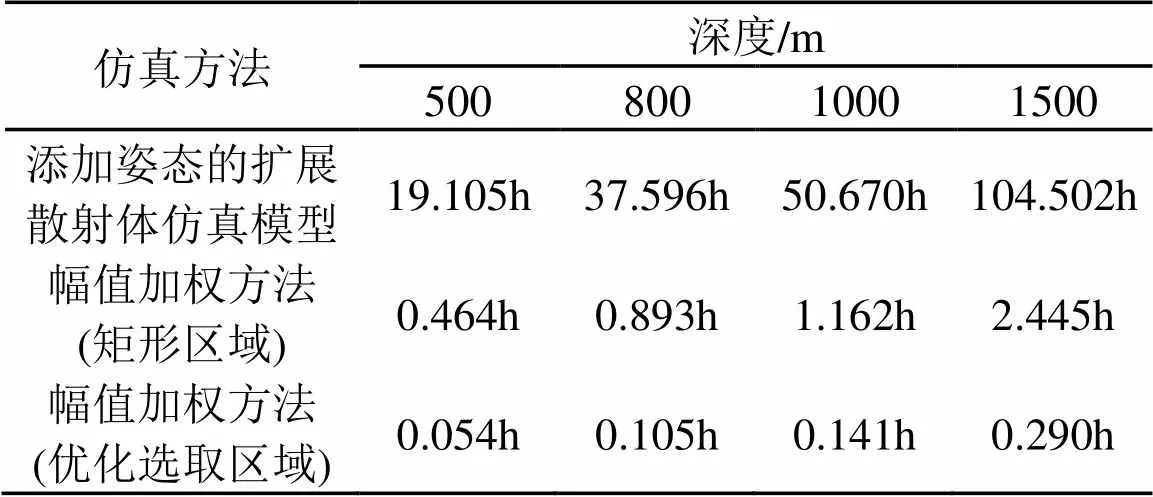
表2 仿真时间对比

4 仿真算法应用

在国产深水多波束测深系统项目中，利用本文提出的海底回波信号快速仿真方法仿真的信号，对三维波束稳定算法和归位算法进行了验证，同时，对深水9发射波束情况进行了仿真，验证了仿真模型的有效性。

4.1 三维波束稳定算法和归位算法验证

图15是实际姿态传感器采集的数据，利用实际传感器数据，假设海底是平坦海底。三维波束稳定算法和归位算法[6]主要用于解决载体姿态引起的多波束测深误差和海底条带杂乱等问题。图16给出了利用仿真数据所得测深条带拼接的对比图，使用波束稳定算法和归位算法前的测深条带分布受载体姿态影响，会有很大程度上的过度稀疏或过度密集，影响成图质量。而采用波束稳定算法和归位算法后的测深条带分布较为均匀，测深条带覆盖范围稳定，有效提高了测深图的质量。

4.2 深水9发射波束情况的仿真

仿真条件：

(1) 水深：4000 m

(2) 发射方向：[-64°,-45°,-32°,-18°, 0°, 18°, 32°, 45°, 64°]

(3) 发射频率：12 kHz

(4) 发射阵：72×12交错排列阵

(5) 接收阵：1×64线阵

(6) 脉冲长度：15 ms

(7) 信号类型：CW，chirp信号

(8) 载体姿态：roll=pitch=yaw=5°

依据上述条件的仿真结果见图17，可以看出，本文的仿真算法对于深水条件下的声呐海底回波信号也可以得到很好的仿真数据(此条件下得到一屏仿真数据普通PC大概需要2 h)。

4.3 相位不一致性

深水多波束测深系统中，发射阵列基元和接收阵列基元的不一致性会引起测深结果的误差。对存在相位不一致性条件下的回波信号的仿真可用于研究校正算法。通过生成发射和接收基元随机模拟基元相位不一致性，图18中给出了接收、发射基元±10°随机相位条件下的测底结果，可以看出，在边缘波束有着较为明显的误差。

5 结论

本文提出了一种既能反映出载体姿态变化又保持较小计算量的深水多波束测深系统海底回波信号仿真方法。在对平坦和非平坦海底的验证中，都有着理想的结果。利用本文的仿真算法，对三维波束稳定算法和归位算法，从仿真角度进行了有效的验证。

本文的仿真方法中没有考虑声速梯度、混响、噪声、衰减等因素，可以进一步完善使之更加贴近实际情况。本文的仿真方法可以用于分析深水多波束测深系统的误差、验证测深或修正算法，可有效地减少研发成本，有着较为广阔的应用前景。

[1] Sintes C, Gueriot D. Interferometric sonar signal simulation through tube tracing[C]// OCEANS 2008-MTS/IEEE Kobe Techno-Ocean. IEEE, 2008: 1-8.

[2] Gueriot D, Sintes C, Garello R. Sonar data simulation based on tube tracing[C]// OCEANS 2007-Europe. IEEE, 2007: 1-6.

[3] Gueriot D, Sintes C. Forward looking sonar data simulation through tube tracing[C]// OCEANS 2010 IEEE-Sydney. IEEE, 2010: 1-6.

[4] Ladroit Y, Sintes C, Lurton X, et al. Extended scatterers model for fast sonar signal simulation[C]// Oceans, 2012-Yeosu. Ieee, 2012: 1-5.

[5] 胡银丰, 朱辉庆, 夏铁坚. 现代深水多波束测深系统简介[J]. 声学与电子工程, 2008(1): 46-48.

HU Yinfeng, ZHU Huiqing, XIA Tiejian. Modern deep water multibeam bathymetric Introduction[J]. Acoustics and Electronics Engineering, 2008(1): 46-48.

[6] 陈若婷, 刘晓东, 刘治宇, 等. 一种基于横摇稳定的多波束测深方法[J]. 声学技术, 2013, 32(5): 368-372.

CHEN Ruoting, LIU Xiaodong, LIU Zhiyu, et al. A bathymetric algorithm based on roll compensation for multi-beam echo sounder[J]. Technical Acoustics, 2013, 32(5): 368-372.

[7] Daniel S, Gueriot D, Maillard E P. Underwater environment restitution through sonar images and swath bathymetry rendering[C]// Systems, Man, and Cybernetics, 1998. 1998 IEEE International Conference on. IEEE, 1998, 5: 4417-4422.

[8] Lurton X. Swath bathymetry using phase difference: theoretical analysis of acoustical measurement precision[J]. IEEE Journal of Oceanic Engineering, 2000, 25(3): 351-363.

A fast simulation method of seabed scattering signal for deep-water multibeam echo sounder

ZHANG Wei1,2, LIU Xiao-dong1, LIU Zhi-yu1, LIU Xiao-gang1, DONG Fei1

(1. Laboratory of Ocean Acoustics Technology,Institute of Acoustics, Chinese Academy of Sciences,Beijng100190, China;2.University of Chinese Academy of Sciences,Beijng100190, China;3.State Key Laboratory of Acoustics,Institute of Acoustics, Chinese Academy of Sciences,Beijng100190,China)

In order to find a balance between the computational time consumption and the accuracy of the physical phenomenon description of simulated sonar signal, this paper presents a fast simulation method of seabed scattering signal based on extended scatters model. Considering the attitude of carrier, the basic idea is using the intensity data of seabed scattering signal to select scatter areas, and then to normalize the scattering intensities from these areas as the amplitude weights of seabed scattering signals to reflect the attitude changes of the transmitting array in the simulated sonar signals. Comparing to the traditional simulation method, the simulation method presented in this paper can reduce the computational complexity and contain attitude information in the signal. Besides, the method can be used to simulate the sonar signal containing phase error information.

deep-water multibeam echo sounder;sonar signal simulation; attitude

TB565

A

1000-3630(2015)-01-0011-07

10.16300/j.cnki.1000-3630.2015.01.003

2014-05-14;

2014-08-24

国家863计划项目(2007AA090901)

张威(1988－), 男, 江苏连云港人, 硕士, 研究方向为信号与信息处理。

刘晓东, E-mail: liuxd@mail.ioa.ac.cn