用三比特GHZ态实现量子稠密编码的方案

麦麦提依明·吐孙， 日比古·买买提明， 阿力木·阿布都拉

（1.新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054；2.新疆莎车县城南双语实验高中，新疆喀什844700）

用三比特GHZ态实现量子稠密编码的方案

麦麦提依明·吐孙1， 日比古·买买提明2， 阿力木·阿布都拉1

（1.新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054；2.新疆莎车县城南双语实验高中，新疆喀什844700）

文章介绍了考虑张三和李四拥有一对三比特最大纠缠态Greenberger-Horne-Zei1inger态（简称GHZ态）来实现量子稠密编码的一种方案，通过此方案有助于研究多体系统中实现量子稠密编码。文章中还介绍从任意三比特系统的密度矩阵约化到两体系统密度矩阵的简单方法。

纠缠态；稠密编码；幺正变换；约化密度矩阵

量子纠缠在量子信息处理过程中起着重要作用，而且量子纠缠的研究对量子信息论的发展有重大的意义［1-5］，因为它在量子信息处理过程中的核心资源，如量子隐形传态［6］，量子稠密编码［7］，量子密钥分配［8］等等。量子稠密编码是目前量子通讯中引起人们关注的研究热点之一，量子稠密编码最早的协议是Bennett和Wiesner提出来的［7］，所谓的量子稠密编码是通过量子纠缠，传送一个量子比特的信息量大于一个经典比特的信息量，而且只使用一个量子比特就可以发送两个比特的经典信息，没有纠缠态的帮助此过程无法实现。近年来，量子稠密编码在理论上［9-13］和实验上［14］都取得了一定的进展，而且发展迅速，取得了很大的成就。Haus1aden等［15］人讨论了从两态系统的稠密编码方案推广到N态系统的稠密编码方案。文章中推导了用GHZ态实现量子稠密编码的方案和相应的相互正交的幺正变换矩阵，最后介绍了从任意三比特系统的密度矩阵推导两比特系统约化密度矩阵的简单方法。在量子信息理论研究中计算多体系统中的密度矩阵是比较难的问题，所以研究三比特系统的量子稠密编码和推导任意三比特系统中约化密度矩阵对多体系统的理论研究具有一定的参考价值。

1 用三比特GHZ态实现量子稠密编码的方案

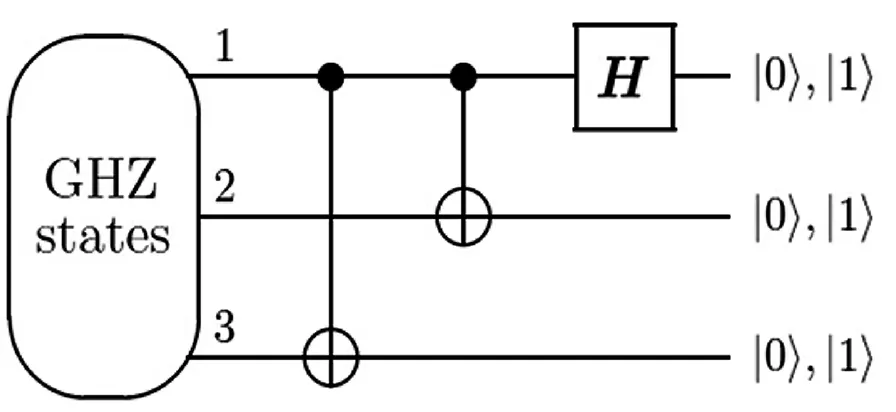
图1 对GHZ态进行测量的量子电路图

三比特量子信道稠密编码［12］的过程为：首先，张三把这3比特的经典信息进行编码，用0，1，2，3，4，5，6，7表示，分别对应000，001，010，011，100，101，110，111。

张三对AB粒子进行幺正变换，表1给出张三对AB粒子的操作以及相应变化结果。

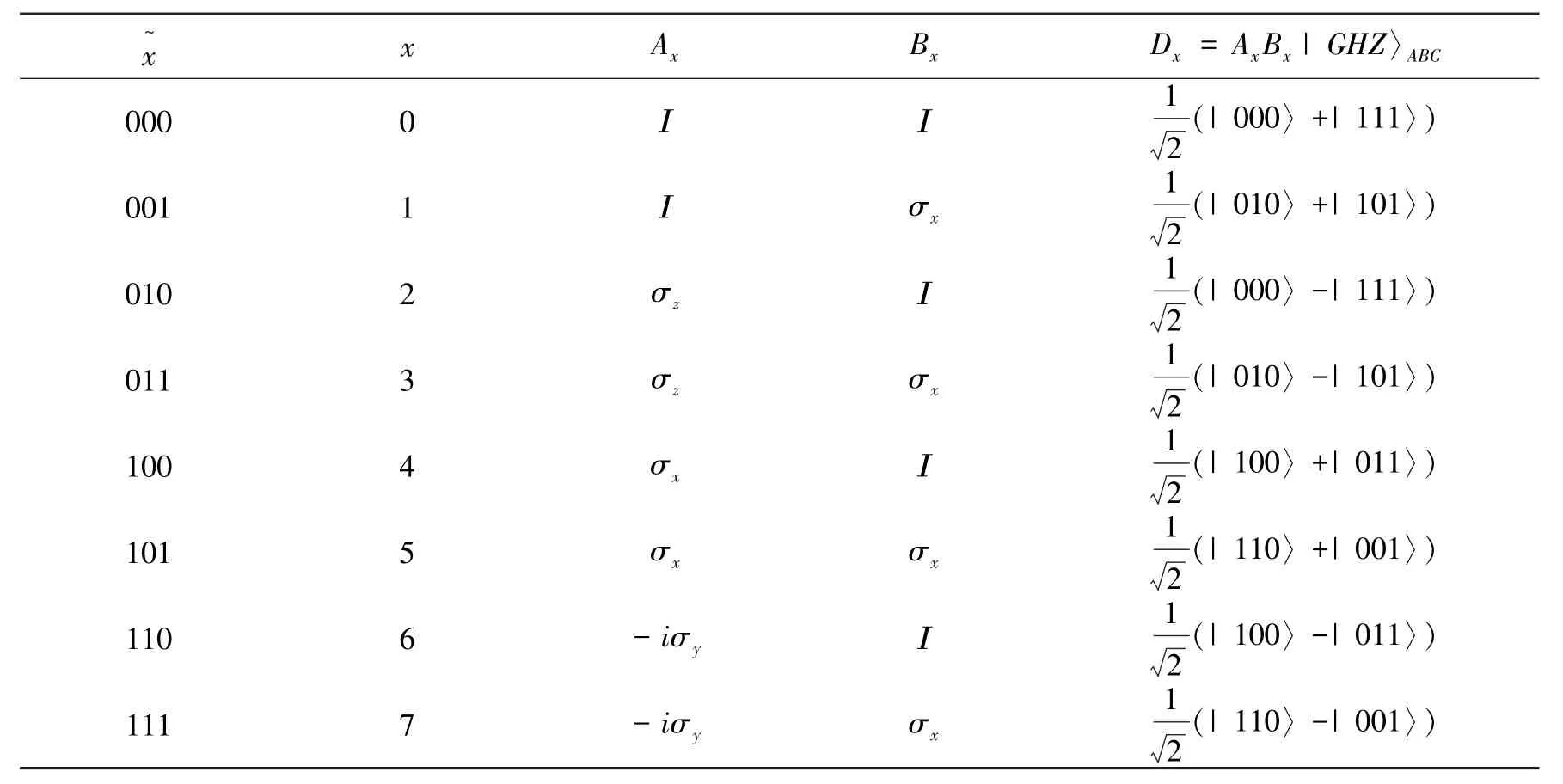
表1 张三对AB粒子的操作及其变化结果

表2 李四执行的幺正变换及其变化结果

表3 李四执行受控非变换及其变化结果

表4 李四对A粒子进行Hadamard变换及其结果

所以，当李四对A粒子进行Hadamard变换后进行测量，根据测量结果就可以完全确定张三传送的是哪一个编码数字，从而得出正确的解码结果。现将解码结果总结如表5所示。

表5 解码结果

2 三比特信道量子稠密编码的幺正变换

在三比特信道量子稠密编码方案中，对两比特量子纠缠态进行编码来实现3比特经典信息的传送。按照文献［15，16］的相互正交的幺正变换公示在三比特系统中实现两字稠密编码的幺正变换可以表示为：

U000|mn〉=|mn〉 U001|mn〉=|m〉⊗|n+1（mod2）〉

U010|mn〉=eiπm|m〉⊗|n〉 U011|mn〉=eiπm|m〉⊗|n+1（mod2）〉

U100|mn〉=|m+1（mod2）〉⊗|n〉 U101|mn〉=|m+1（mod2）〉⊗|n+1（mod2）〉

U110|mn〉=eiπm|m+1（mod2）〉⊗|n〉 U111|mn〉=eiπm|m+1（mod2）〉⊗|n+1（mod2）〉

其中，|mn〉=|m〉⊗|n〉，（m，n=0，1）。具体的幺正变换矩阵［16］是：

U000=Ι⊗Ι；U001=Ι⊗σx；U010=σz⊗Ι；U011=σz⊗σx；

U100=σx⊗Ι；U101=σx⊗σx；U110=-iσy⊗Ι；U111=-iσy⊗σx

编码以后的量子态可以表示为：

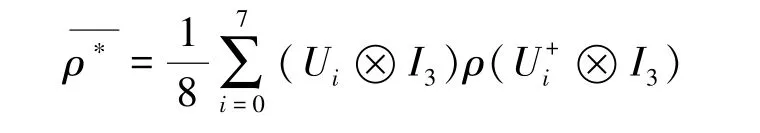
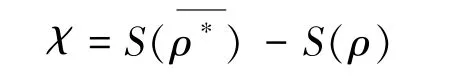
在此方案中，利用两个量子比特纠缠态实现了3比特经典信息的传送，因此得出来的最大信道容量应该是3，是经典信道容量的1.5倍。Ui是作用在第1，2两个量子比特上的幺正变换。信道容量还是用Ho1evo量［17，18］表示：

3 三比特系统的约化密度矩阵的推导

任意个三比特系统密度矩阵在标准基下的矩阵可以表示为：

然后把任意个三体系统A，B和C的密度矩阵用矩阵元表示为：

其中

按照上式AB系统的约化密度矩阵表示为：

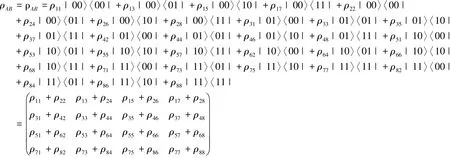
4 结 论

通过研究三比特系统中实现量子稠密编码的方案，得出三比特系统跟两比特系统同样适合用纠缠态来实现稠密编码，同时研究多体系统具有一定的理论依据。还推导了三比特密度矩阵推导两比特约化密度矩阵的简单公式，此结果有助于理论研究者把复杂的多体系统的情形简化到两体系统的情况来研究多体系统，具有一定的参考价值。

［1］Raussendorf R，Briege1H J.A one-way quantum computer［J］.Phys.Rev.Lett.2001，86（22）：5188-5192.

［2］Xiang BW，et a1.Quantum information with Gaussian states［J］.Phys.Rep.2007，448（1-4）：1-111.

［3］Long G L，et a1.Quantum secure direct communication and deterministic secure quantum communication［J］.Front.Phys.Chin.2007，2（3）：251 -272.

［4］WAN Hong-bo，YE Liu.Scheme for imp1ementing quantum dense coding by using 1inear optica1system［J］.Chinese Journa1of Quantum E1ectronics，2010，27（2）：161-166.

［5］Jin R B，Chen L B，Wang F Q，Su Z K Genera1and Optima1Scheme for Loca1Conversion of Pure States［J］.Chin.Phys.Lett，2008，25（6）：1957.

［6］Bennett C H，Brassard G，Brassard C，Jozsa R，Peres A，WoottersW K.Te1eporting an unknown quantum state via dua1 c1assica1and Einstein-Podo1sky-Rosen channe1s［J］.Phys.Rev.Lett，1993，70：1895.

［7］Bennett CH，Wiesner S J.Communication via one-and two-partic1e operators on Einstein-Podo1sky-Rosen states［J］.Phys.Rev.Lett，1992，69：2881.

［8］Ekert A K.Quantum cryptography based on Be11's theorem［J］.Phys.Rev.Lett.1991，67：661.

［9］Bareno A，Ekert A K.Dense Coding Based on Quantum Entang1ement［J］.Mod.Opt.1995，42：1253-1259.

［10］Braunstein S L，Kimb1e H J.dense coding for continuous variab1es［J］.Phys.Rev.A，2000，61（4）：042302.

［11］Bose S，P1enio M B，Vedra1V.Mixed state dense coding and its re1ation to entange1ementmeasures［J］.Mod.opt.2000，47：291.

［12］Hyuk-jae L，Doyeo1A and Sung W H.Dense coding in entang1ed states［J］.Phys.Rev.A，2002，66：024304.

［13］Guo F Z.ffect of anisotropy on optima1dense coding［J］.Phys.Scr.，2009，79：015005.

［14］Matt1e K，Weinfurter H，Kwiat PG and Zei1inger A.Dense coding in Experimenta1Quantum Communication［J］.Phys.Rev.Lett.，1996，76：4656.

［15］Haus1aden P，Jozsa R，Schumacher B，Westmore1and M and WoottersW K.C1assica1 information capacity of a quantum channe1［J］.Phys.Rev. A 1996，54（3）：1869.

［16］Gorbachev V N，Trubi1ko A I，Rodichkina A A，Zhi1iba A I.Te1eportation and dense coding via amu1tipartic1e quantum channe1of the GHZ-c1ass［J］.Quantum.Inf.Comput.，2002，2（5）：367-378.

［17］Tohya H.Optima1dense coding with mixed state entang1ement［J］.Phys.A：Math.Gen，2001，34：6907.

［18］Bose S，P1enio M B and Vedra1V.Mixed state dense coding and its re1ation to entang1ementmeasures［J］.J.Mod.Opt.，2000，47（2-3）：291.

［19］曾瑾言，量子力学［M］.北京：科学出版社，2007：25-34.

The Scheme of Dense Coding Using Three Qubit GHZ States

TursunMAMTlMlN1， Mam tim in RABlGUL2， WANG Fei1
（1.College ofPhysics and Electronic Engineering，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）2.XinJiang Yarkant Bilingual Experimental High School，South of the City，Kashgar，Xinjiang 844700，China）

This artic1e introduced the scheme of Zhang San and Li Sihas a pair of three bits 1argest entang1ed Greenberger-Horne-Zei1inger state（GHZ state）to achieve a quantum dense coding，through this scheme wi11 he1p rea1ize quantum dense coding in mu1tibody system.This artic1e a1so introduces simp1emethod of any three bits system's densitymatrix reduces to two bits densitymatrix.

Entang1ement；Dense coding；Unitary transformation；Reduced density matrix

O431.2

A

1008-9659（2015）04-065-06

2015-07-03

新疆维吾尔自治区高校科研计划青年教师科研启动基金项目（XJEDU2014S035）；新疆维吾尔自治区理论物理重点学科招标课题（14XSQZ0602）资助的课题。

麦麦提依明·吐孙（1986-），男，新疆乌鲁木齐人，讲师，主要从事量子信息与量子计算方向的研究。