基于机构运动学的多连杆悬架下控制臂优化

林涌周 王仲宜 谷玉川 廖美颖

（广州汽车集团股份有限公司汽车工程研究院）

汽车悬架控制臂的开发需要满足空间、强度、工艺及成本要求。目前该开发工作主要依赖于参照现有方案和对标同级别车型等方式进行设计，容易出现空间动态干涉和材料厚度盈余等缺陷，无法达到轻量化设计与成本控制要求[1-2]。文章提出将机构运动学与有限元优化相结合的方法，综合运用拓扑优化与尺寸优化技术，获得满足空间和强度约束条件下控制臂的轻量化设计方案，提高了开发设计的可行性与可靠性。

1 理论模型

1.1 机构运动学模型

机构运动学仿真是对数字样机空间运动的模拟技术，已成为汽车悬架系统开发及零部件设计的重要开发工具与校核手段[3-4]。采用机构运动学方法建立悬架系统模型，需要满足式（1）所示系统自由度。

式中：N——悬架系统运动部件数量；

fi——各运动副约束自由度数量；

FD——悬架系统驱动自由度数量。

1.2 拓扑优化有限元模型

拓扑优化是在给定设计空间内求解最优材料分布的仿真技术[5-6]，常用拓扑优化方法包括生死单元法、均匀化法与变密度法等[7-8]。OptiStruct软件基于变密度法数学模型，将单元材料密度作为设计变量在0～1之间连续变化，求解满足特定约束条件下目标函数的最优解。其中目标函数根据不同设计需求选取，如质量、体积及应变能等。约束条件可选择结构体积比、单元应力应变及材料屈服极限等设计指标。变密度法的拓扑优化数学模型，如式（2）所示。

式中：d——单元材料体积质量（无量纲）；

N——约束条件数量；

f（d），V（d）——拓扑优化约束和目标函数。

1.3 尺寸优化有限元模型

尺寸优化是在设计结构形成初步方案基础上开展设计参数优化的细节设计方法[5]。该方法通过改变结构单元属性，如单元厚度和截面属性等，求解满足一定约束条件下目标函数最优解，从而确定设计参数的最优方案选择。其数学模型，如式（3）所示。

M，N——设计变量和约束条件的数量；

fj（X），V（X）——尺寸优化约束和目标函数。

2 优化设计方法

2.1 运动包络设计

2.1.1 运动学模型建立

将所开发多连杆后悬架三维模型导入CATIA软件，构建系统零部件及运动副拓扑关系，如图1所示，图1中括号内数字为对应运动副约束自由度数。

依次搭建悬架系统DMU模型，如图2所示。模型共包含运动部件11个（系统自由度数为66，其中车身安装点为固定部件），运动副16个（约束自由度数为65），按照车型悬架行程设计要求，在车轮轮心处施加轮跳驱动（驱动自由度数为1），所建立DMU模型满足式（1）。

2.1.2 初始设计域构建

基于所建立的悬架系统运动学DMU模型驱动仿真，以下控制臂为包络运动参考输出相关零部件的运动包络，即得到了其他零部件相对后下控制臂的运动包络，进而在CATIA装配模块下重新以控制臂为固定零件，将所获得的运动包络依次装配形成新的悬架模型，如图3所示，即构成了后下控制臂的空间包络约束。

下控制臂与周边件运动包络之间的位置重叠即为悬架运动过程中的空间干涉，而两者的最小空间距离即等效为运动过程中的最小间隙。按照悬架系统设计要求，设置下控制臂与周边件的最小动态间隙（10 mm），通过空间包络约束与悬架动态间隙的叠加，经过曲面设计与特征构建，优化得到下控制臂的几何设计空间，作为拓扑优化的初始设计域，如图4所示。

2.2 拓扑优化设计

2.2.1 优化设计建模

将运动包络设计获得的下控制臂几何设计空间导入HyperWorks软件OptiStruct模块进行有限元建模。采用CTETRA四面体单元进行网格划分，设定单元最小尺寸为3mm，获得的有限元模型包含节点36267个，单元168 780个。单元材料选用QSTE380，弹性模量为205 GPa，泊松比为0.3，材料屈服极限为380 MPa。

1）载荷边界条件设定。根据控制臂装配关系和载荷加载形式，将下控制臂前后衬套内表面节点通过RBE2单元连接到衬套中心点处，综合考虑下控制臂与车身连接的柔性特性，释放前衬套点前进方向平移自由度，即约束后衬套A处1～6自由度，约束前衬套B处2～6自由度。下控制臂在转向节球销C处、竖拉杆衬套中心点D处通过衬套承受节点载荷（载荷值，如表1所示），建立拓扑优化设计的载荷边界条件设定，如图5所示。

2）优化设计空间定义。为了保证装配位置的强度，将下控制臂与转向节、竖拉杆及车身连接区域定义为非设计区域，其余本体结构为设计区域，得到的优化设计空间定义，如图6所示。

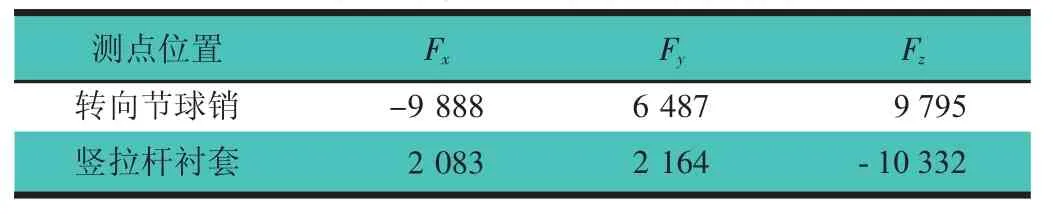
表1 典型行驶工况下加载点极限载荷 N

2.2.2 拓扑优化求解分析

针对建立的下控制臂拓扑优化设计模型（如图7所示），在OptiStruct完成拓扑优化参数定义，其中：

目标函数：最小化下控制臂重量；

设计变量：本体单元材料体积质量；

响应参数：单元的Von-Mises应力；

约束条件：材料屈服局限为约束条件，即响应参数上限值为380 MPa。

根据定义的优化模型开展拓扑优化问题的求解，模型经过15次迭代计算后收敛，取单元密度阈值为0.15，得到单元密度拓扑分布云图，如图8所示。

2.3 尺寸优化设计

2.3.1 几何模型建构

将拓扑优化结构得到的下控制臂基本拓扑构型，利用OptiStruct的OSSMooth工具导出IGES文件，并结合选定的冲焊成型工艺要求，在CATIA软件中开展概念设计阶段的几何模型建构。

考虑制造工艺及成本控制要求，将下控制臂本体分为上下钢板冲压后拼焊成型，转向节安装支架采用冲压成型后与本体焊接成型，并结合工艺与加工定位需要，在下控制臂本体面设计加强筋及工艺孔，最终获得下控制臂的基本几何构型，如图9所示。

2.3.2 尺寸优化求解分析

在确定了下控制臂的基本几何构型后，需要进一步确定各组成部分的材料厚度，以减少材料冗余，实现轻量化设计与成本控制的目标。在OptiStruct软件中完成尺寸优化模型的建立，其中：

目标函数：最小化下控制臂重量；

设计变量：设计变量及其参数范围，如表2所示；

响应参数：单元的Von-Mises应力；

约束条件：材料屈服局限为约束条件，即响应参数上限值为380 MPa。

根据定义的优化模型开展尺寸优化问题的求解，模型经过6次迭代计算后收敛，优化后下控制臂单元厚度结果见表2，即得到了下控制臂的优化设计模型。

3 优化方案验证

3.1 强度校核

为了进一步验证优化方案的可靠性与合理性，需要开展行车典型工况下控制臂优化设计方案的强度校核[9-10]。针对汽车行驶过程中4种典型工况（加速右转、加速起步、前进制动及倒车制动），开展下控制臂强度校核，获得典型工况下控制臂应力云图，如图10所示。

从图10中可以看到，在4种典型工况条件下，下控制臂单元应力均满足材料屈服极限要求，且均未出现明显应力集中，即下控制臂优化设计方案模型满足强度设计要求。

3.2 模态校核

汽车控制臂的固有频率与悬架系统振动特性有直接关系，需要避开悬架系统的共振区间。对于多连杆悬架下控制臂，一般要求自由状态1阶弹性体固有频率超过500 Hz，约束状态下1阶固有频率超过350 Hz[10]。对设计优化方案以此开展模态分析进行固有频率校核，得到下控制臂在自由状态和约束状态下的固有频率，如表3所示。

表3 下控制臂优化方案模态校核结果 Hz

从表3可以看到，下控制臂在自由状态和约束状态下均有效避开了设计共振区，满足模态设计要求。

3.3 台架试验与实车验证

为了进一步验证下控制臂强度与疲劳耐久性，按照优化设计方案制成样件并开展台架试验与装车验证。其中台架试验将车身连接衬套固定，在转向节安装中心点加载极限载荷，经过10万次疲劳耐久试验下控制臂本体未出现结构开裂或失效；样件装车试验经过10万km路试，下控制臂本体及支架均未出现失效或显著变形，结构强度和疲劳耐久性满足设计要求。

4 结论

以多连杆后悬架下控制臂为研究对象，通过构建悬架运动行程内周边零部件的运动包络，获得下控制臂优化设计的初始设计域；综合运用拓扑优化和尺寸优化技术，结合制造工艺和成本控制要求，获得控制臂的优化设计方案；通过典型工况强度校核、模态校核与台架实车测试验证了方案的可行性和可靠性，实现了满足运动空间和强度要求下控制臂的正向设计。文章提出的优化设计方法能够为汽车悬架零部件的轻量化设计提供参考。