基于堰前最高水位最大熵分布的施工导流风险模拟方法

雷 畅,胡志根,刘 全

(武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)

基于堰前最高水位最大熵分布的施工导流风险模拟方法

雷 畅,胡志根,刘 全

(武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)

为直观描述围堰运行期导流风险率函数,准确进行施工导流风险评估,利用洪峰和洪量联合分布,以熵最大为原则推求最高水位分布密度函数,结合导流建筑物泄流不确定性,随机模拟堰前最高水位序列,提出了基于堰前最高水位最大熵分布的施工导流风险模拟方法,并计算导流风险率。实例分析表明,该方法模拟的施工洪水能较好地反映实测洪水系列,所推求的堰前最高水位分布密度函数合理,能弥补传统施工导流风险模拟难以反映围堰使用近期实测洪水过程真实情况的不足,在保证准确性的前提下提高了风险计算效率与普适性,可为施工导流风险分析与方案决策提供依据。关键词：围堰;施工导流;风险模拟;联合分布;最大熵分布

施工导流风险分析是导流方案决策的重要环节,国内外许多学者对此进行了深入细致的研究。周宜红等[1]基于调洪演算和围堰堰前水位变化的随机微分方程,建立与堰前水位变化直接联系的风险率模型,较全面地反映了施工导流系统的影响因素,但堰前水位的分布推求困难,单纯采用解析方法难以满足精度要求。胡志根等[2-3]提出利用蒙特卡罗方法(Moute-Carlo,M-C法)仿真模拟围堰调洪过程,确定堰前水位变化过程及其分布函数。钟登华等[4-5]、李传奇等[6]分别采用系统结构图、超立方抽样-蒙特卡罗方法(LHS-MC)提高仿真模拟的运算效率,改进仿真模型的通用性。以上研究在模拟施工洪水时仅以单一变量(洪峰或洪量)的统计特征值作为控制标准,往往导致模拟洪水系列洪峰与洪量的统计特征值不能同时与实测洪水系列保持一致,无法准确反映实测洪水过程。为此,张超等[7-8]直接根据实测洪水得到堰前年最高水位序列,采用信息熵法推求其分布函数,但未考虑施工导流系统影响因素的随机性,不可避免地带来了误差,且当实测洪水样本容量小时,所求分布函数的精度难以保证。

本文利用Copula函数构造峰量联合分布模拟施工洪水过程,耦合泄流不确定性,模拟堰前最高水位序列,基于最大熵原理推求序列的密度函数,提出一种新的导流风险模拟方法,并与M-C法和P-Ⅲ分布法进行比较。

1 堰前最高水位分布模拟

1.1 施工洪水的模拟

Copula函数是边缘分布为[0,1]区间均匀分布的联合分布函数,能独立于随机变量的边缘分布反映随机变量的相关性结构,且模拟序列能较好地保持原序列的统计特征[9]。本文采用Gumbel-Hougaard Copula描述洪峰和洪量的相关性,模拟联合重现期对应的施工洪水过程,表达式[10]如下:

(1)

式中:F(q,w)为洪峰q和洪量w的联合分布函数;Fq(q)、Fw(w)分别为q和w的边缘分布函数,假设均服从P-Ⅲ型分布;θ为Copula函数参数。

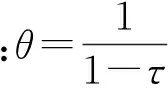
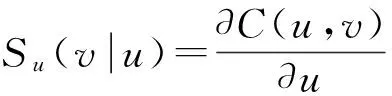
1.2 堰前最高水位序列的模拟

堰前最高水位主要由施工洪水与导流建筑物的泄流能力共同控制。其中,施工洪水峰量联合分布服从[0,1]上的均匀分布;导流建筑物的泄流能力受泄流建筑物糙率的影响,一般服从不对称三角形分布。堰前最高水位序列{z1，z2，…，zN}可基于M-C随机抽样方法通过调洪演算计算生成。

1.3 堰前最高水位分布的拟定

基于堰前最高水位序列推求其分布规律属于不适定问题,受主观因素和样本数量影响较大,采用最大熵原理确定概率分布,能使数据不足引起的人为假定影响最小化,同时保证解析结果的一致性[13]。假设已得到N个堰前最高水位样本{z1,z2,…,zN},可建立如下优化模型:

maxS=-max∫Ωf(z)ln[f(z)]dz

(2)

(3)

式中:S为堰前最高水位z的信息熵;f(z)为z的概率分布的密度函数;rz,i为z的第i阶原点矩；m为z的原点矩的阶数,一般取3～5;Ω为z所在的集合{z1,z2,…，zN}。

引进Lagrange乘子λi,令其对f(z)的变分为0,并用λ0替代λ0+1,导出熵S最大时f(z)的表达式为

(4)

参数λ1、λ2、…、λm可采用极大似然估计法进行求解,λ0为λ1、λ2、…、λm的函数:

(5)

该密度函数的极大似然估计如下:

(6)

将极大似然估计函数取对数,对λi求偏导,并令其为0,可得

(7)

求解该m次非线性方程组得λ1、λ2、…、λm,代入式(5)可求λ0。

2 基于最大熵原理的施工导流风险模拟

按最大熵原理推求概率密度函数的精度取决于样本容量及其上下界值的选定。为同时保证计算精度与效率,计算过程逐步增大样本容量,当改变样本容量对频率值没有影响,即频率值收敛时,选定该样本容量作为计算样本容量。

本文风险率计算的主要步骤如下:

a. 按照峰量联合分布函数、泄流能力分布产生随机数,拟合n1组施工洪水过程线和泄流过程线。

b. 仿真计算围堰堰前最高水位序列{z1，z2,…,zN}。

c. 计算每一个堰前水位样本落入各个指定区间的频率Pn1,k(k=1,2,…,s),s为划分的区间数。

d. 重复步骤a～c,再次生成大于n1的样本容量为n2的堰前水位序列,并计算Pn2,k,按式(8)计算判断,若δ<1则认为所选取的样本容量满足计算精度要求;否则需增大样本容量值,重复步骤a～d,直至满足要求为止,并将最终选定的样本容量计为N。

(8)

e. 对N个堰前最高水位样本{z1,z2,…,zN},计算其m阶原点矩(一般为3～5阶,根据拟合结果选择),由式(2)～(4)计算其分布密度函数f(z)。

f. 假定围堰设计挡水位为Z0,计算导流风险率:

(9)

3 实例分析

3.1 工程概况

某航电枢纽工程正常蓄水位183 m,总库容3.72亿m3。大坝采用混凝土重力坝,坝顶高程205.5 m,工程等别为二等,工程规模为大(2)型。根据各个导流时期导流建筑物保护对象的级别,自身的使用年限以及围堰的高度和堰前库容等指标,参考DL/T 5397—2007《水电工程施工组织设计规范》,选定的导流建筑物级别为4级临时建筑物,明渠泄流,土石围堰全年挡水,导流标准为全年10年一遇,洪峰流量为20 900 m3/s,上游围堰设计挡水位为188.5 m。洪峰流量均值及其Cv、Cs/Cv分别为13 700 m3/s、0.38、3.5；7天洪量均值及其Cv、Cs/Cv分别为46.2亿m3、0.48、3.5；泄流能力随机参数的上、中、下限值分别为1.05、1.00、0.95。

3.2 施工洪水分析与拟定

根据坝址提供的54年洪水过程资料,计算洪峰序列与年最大7 d洪量序列的kendall秩相关系数τ=0.771 5,Copula函数参数θ=4.376,可知其具有较高的相关性,统计量D=0.0713,通过K-S检验。联合分布函数表达式为

C(u,v)=exp{-[(-lnu)4.376+(-lnv)4.376]1/4.376}

(10)

3.3 堰前最高水位概率分布拟定

通过调洪演算生成大量样本数据,模拟800次后,样本容量满足计算精度要求,密度函数经过K-S检验,满足置信度0.05的要求,其表达式为

f(z)=exp(-18 678+405.66z-3.309z2+

0.012z3-0.000 05z4)

(11)

3.4 风险率计算

根据导流风险模型对堰前最高水位分布密度函数积分得到风险率,并与M-C法以及P-Ⅲ分布法进行对比分析,各方法得到的导流风险率如图1和表1所示。

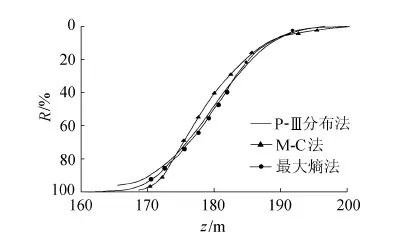
图1 堰前最高水位-导流风险率关系曲线

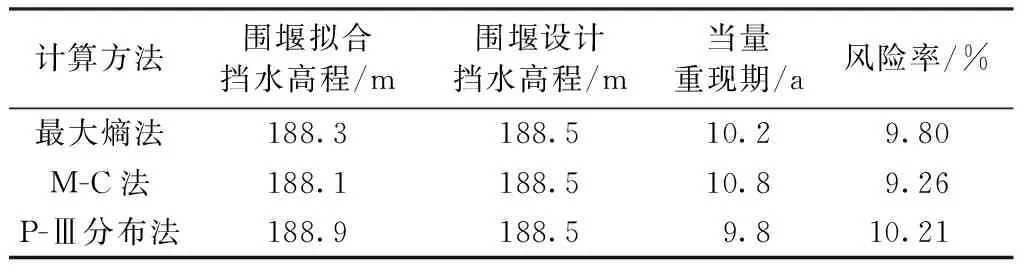
计算方法围堰拟合挡水高程/m围堰设计挡水高程/m当量重现期/a风险率/%最大熵法188.3188.510.29.80M-C法188.1188.510.89.26P-Ⅲ分布法188.9188.59.810.21

采用M-C法计算施工导流风险时,计算结果随模拟次数的增加缓慢收敛,如表2所示。

表2 基于M-C法的风险率

3.5 结果分析

a. M-C法的计算精度在一定程度上取决于模拟次数,由表2可知M-C法模拟20 000次后结果才收敛,最大熵法仅需800次,计算效率优于M-C法。

b. 由表1和图1可知最大熵法较M-C法与P-Ⅲ分布法得到的导流风险率更为接近,对围堰使用近期堰前最高水位序列及其分布的模拟效果更优。这主要是因为最大熵法和P-Ⅲ分布法均基于近期实测洪水资料,且前者利用峰量联合分布模拟施工洪水,可保证峰和量的统计特征值同时与实测系列保持一致,M-C法使用的是考虑历史洪水影响的设计洪水且仅以洪峰统计特征值作为随机模拟的控制参数,难以反映围堰运行期施工洪水的真实情况。

c. 虽均基于实测洪水信息,最大熵法和P-Ⅲ分布法得到的风险率也存在差异。一是因为最大熵法考虑了洪峰和洪量的相关性、峰量组合的随机性以及泄流的随机性对施工洪水、泄流能力进行模拟,P-Ⅲ分布法直接根据实测洪水样本和单一泄流曲线进行调洪演算,未考虑施工导流过程中的不确定性因素;二是因为堰前水位是受人工影响和干预后的非自然序列,其概率分布是一个随机系统,因假定的分布函数形式不同而有所差异。

4 结 语

本文提出基于最大熵原理构建堰前最高水位分布的导流风险模拟方法。该方法利用峰量联合分布随机模拟施工洪水过程,能较好地反映实测洪水系列,弥补了单一变量描述施工洪水过程的局限性;随机模拟堰前最高水位序列,克服了直接根据实测洪水得到堰前最高水位的样本容量小、概率分布函数精度难以保证的缺点,且对风险影响因素考虑得更为全面;应用最大熵原理推求概率分布函数,提高了风险计算效率并避免了传统堰前最高水位概率分布函数确定的随意性。实例分析表明,该方法的计算结果是准确和合理的,可应用于施工导流风险计算与方案决策。

[ 1 ] 周宜红,肖焕雄.导流围堰施工计划的动态概率设计方法[J].水利学报,1997(10):59-62.(ZHOU Yihong,XIAO Huanxiong.Dynamic-probability-based design of constructional planning of cofferdam[J].Journal of Hydraulic Engineering,1997(10):59-62.(in Chinese))

[ 2 ] 胡志根,刘全,贺昌海,等.基于Monte-Carlo方法的土石围堰挡水导流风险分析[J].水科学进展,2002,13(5):634-638.(HU Zhigen,LIU Quan,HE Changhai,et al.Risk analysis of retaining rockfill cofferdam for diversion based on the Monte-Carlo method[J].Advances in Water Science,2002,13(5):634-638.(in Chinese))

[ 3 ] TINGSANCHALI T,BOONYASIRIKUL T.Stochastic dynamic programming with risk consideration for transbasin diversion system[J].Journal of Water Resources Planning and Management,2006,132(2):111-121.

[ 4 ] 钟登华,黄伟,张发瑜.基于系统仿真的施工导流不确定性分析[J].天津大学学报,2006,39(12):1441-1445.(ZHONG Denghua,HUANG Wei,ZHANG Fayu.Uncertainty analysis for construction diversion based on system simulation[J].Journal of Tianjin University,2006,39(12):1441-1445.(in Chinese))

[ 5 ] 钟登华,黄伟,李玉钦.面向结构图的施工导流系统仿真研究[J].系统仿真学报,2008,20(1):191-195.(ZHONG Denghua,HUANG Wei,LI Yuqing.Structural drawing oriented simulation method of construction diversion system[J].Journal of System Simulation,2008,20(1):191-195.(in Chinese))

[ 6 ] 李传奇,王帅,王薇,等.LHS-MC方法在漫坝风险分析中的应用[J].水力发电学报,2012,31(1):5-9.(LI Chuanqi,WANG Shuai,WANG Wei,et al.Overtopping risk analysis using LHS-MC method[J].Journal of Hydroelectric Engineering,2012,31(1):5-9.(in Chinese))

[ 7 ] 张超,胡志根,刘全.基于最大熵原理的施工导流随机模糊风险分析[J].四川大学学报:工程科学版,2012,44(9):59-63.(ZHANG Chao,HU Zhigen,LIU Quan.Random fuzzy risk analysis of construction diversion based on maximum entropy principle[J].Journal of Sichuan University:Engineering science edition,2012,44(9):59-63.(in Chinese))

[ 8 ] 张超,胡志根,刘全.基于实测洪水系列和最小熵方法的施工导流风险[J].武汉大学学报:工学版,2012,45(3):296-300.(ZHANG Chao,HU Zhigen,LIU Quan.Construction diversion risk analysis based on observed flood series and minimum entropy method[J].Engineering Journal of Wuhan University,2012,45(3):296-300.(in Chines))

[ 9 ] 周研来,梅亚东,张代青.一种新的径流过程随机模拟方法[J].水利水电科技进展,2011,31(3):9-12.(ZHOU Yanlai,MEI Yadong,ZHANG Daiqing.New stochastic simulation method for streamflow hydrographs[J].Advances in Science and Technology of Water Resources,2011,31(3):9-12.(in Chinese))

[10] SALVADORI G,MICHELE C D.Frequency analysis via copulas theoretical aspects and applications to hydrological events[J].Water Resources Research,2004,40(12):1-17.

[11] 肖义.基于Copula函数的多变量水文分析计算研究[D].武汉:武汉大学,2007.

[12] 肖义,郭生练,熊立华,等.一种新的洪水过程随机模拟方法研究[J].四川大学学报:工程科学版,2007,39(2):55-60.(XIAO Yi,GUO Shenglian,XIONG Lihua,et al.A new random simulation method for constructing synthetic flood hydrographs[J].Journal of Sichuan University:Engineering science edition,2007,39(2):55-60.(in Chinese))

[13] 刁艳芳,王本德,刘冀.基于最大熵原理方法的洪水预报误差分布研究[J].水利学报,2007,38(5):591-595.(DIAO Yanfang,WANG Bende,LIU Ji.Study on distribution of flood forecasting errors by the method based on maximum entropy[J].Journal of Hydraulic Engineering,2007,38(5):591-595.(in Chinese))

Construction diversion risk simulation method based on maximum entropy distribution of the highest water level in weir//

LEI Chang, HU Zhigen, LIU Quan

(StateKeyLaboratoryofWaterResourcesandHydropowerEngineeringScience,WuhanUniversity,Wuhan430072,China)

Based on maximum entropy distribution of the highest water level in weir, in this paper we present a simulation method of construction diversion risk that intuitively describes the diversion risk rate function of operational cofferdam and accurately assess construction diversion risk. In our method, the highest water level distribution density function is derived by using the distribution of flood peak and flood volume with the maximum entropy principle. Meanwhile, combining the discharge uncertainty of diversion buildings, the method stochastically simulates the highest water level sequence in weir. Then the method is employed to calculate diversion risk rate. The analysis shows that the simulated construction flood can well reflect the measured flood series. Moreover, the derived distribution density function of the highest water level in weir is reasonable, which can fully reflect true situation of recent measured flood in weir compared with traditional methods. On the premise of accuracy, this method improves risk calculation efficiency and applicability. Therefore, the method provides support for risk analysis and program decisions of construction diversion.

weir; construction diversion; risk simulation; joint distribution; maximum entropy distribution

国家自然科学基金(51279137,51379164)

雷畅(1990—),女,湖北松滋人,硕士研究生,主要从事施工导流风险分析与决策研究。E-mail:aimeelei@whu.edu.cn

10.3880/j.issn.1006-7647.2015.03.006

TV551.1

A

1006-7647(2015)03-0030-04

2014-03-10 编辑：郑孝宇)