狼群算法在水电站水库优化调度中的应用

王建群,贾洋洋, 肖庆元

(河海大学水文水资源学院,江苏 南京 210098)

狼群算法在水电站水库优化调度中的应用

王建群,贾洋洋, 肖庆元

(河海大学水文水资源学院,江苏 南京 210098)

为探讨水电站水库优化调度问题求解的新方法，对狼群算法及其在水电站水库优化调度中的应用进行了研究。对狼群算法中的围攻算法进行了改进，给出了水电站水库优化调度问题的狼群算法设计及求解步骤。基于水电站水库优化调度实例，对狼群算法的敏感参数奔袭步长进行了模拟计算和分析，给出了奔袭步长的有效取值范围。实例计算结果表明，狼群算法是一种求解水电站水库优化调度问题的有效方法。

狼群算法；群体智能算法；水电站；水库优化调度

为解决各种复杂的非线性优化问题,很多学者提出了模拟生物群体智能的算法,如遗传算法[1]、蚁群算法[2]、粒子群算法[3]等。由于这些算法在求解时不依赖于目标函数的梯度信息,因而特别适用于传统方法解决不了的大规模复杂优化问题。但由于优化问题的多样性和复杂性,这些群体智能算法在不同的应用场合仍会存在一些不足,如早熟、收敛精度不高、易陷入局部最优等问题[4]，为此Yang等[5]于2007年提出了一种新的仿生狼群捕食行为的群体智能优化算法——狼群算法(wolf pack search algorithm,WPS)。狼群算法不同于以前的群体智能优化算法,它同时具有3个不同的搜索能力:模拟狼群个体的游猎行为，即竞争领导者狼行为，体现了算法具有独立的局部精细搜索能力；模拟狼群的召唤行为，即向领导者移动行为，提高了算法的局部最优解的搜索效率；模拟狼群的攻击行为，即包围猎物的行为及狼群竞争更新的行为，保证了算法能收敛到全局最优解。Liu等[6]将狼群算法分为模拟狼群的游猎行为、攻击行为、狼群竞争更新等3个主要步骤。Tang等[7]认为狼群算法主要包括模拟狼群搜索猎物和遇到威胁逃逸行为2个计算步骤。周强等[8]提出了一种基于领导者策略的狼群搜索算法,将狼群算法总结为竞争领导者狼、向领导者移动、包围猎物、狼群竞争更新等4个主要步骤,给出了新的围攻行为即包围猎物行为的表达式。Li等[9]于2014年将狼群搜索算法和支持向量机技术相结合并应用于糖尿病患者外周血管闭塞估计问题。水电站水库优化调度是一个多阶段、非线性的连续优化问题,传统的求解方法是动态规划法及其改进算法[10]，但随着水库数目的增加,或为了提高计算精度而增加决策变量离散点数目,动态规划法会增加计算机系统资源量的占用而出现维数灾问题[11]。近年来,遗传算法、粒子群算法等群体智能算法由于对求解问题的限制较少、不需离散决策变量、容易实现等优点而被应用于水库优化调度中[12-13]。狼群算法作为一种新颖的群体智能算法,目前还没有应用于水库优化调度中。本文对狼群算法及其在水电站水库优化调度中的应用进行研究,探讨狼群算法应用于水库优化调度中的可行性和有效性。

1 算法基本原理

经研究发现,狼群在捕猎时具有严密的组织系统,分工明确、步调一致,以保证行动的高效性,齐心协力战胜比自己强大的对手,最终捕获猎物。狼群在捕猎过程中,首先派出少数精壮的狼在各自的活动范围内进行游猎;发现猎物的狼通过嚎叫召唤同伴向它奔袭、包围猎物;最后通过优胜劣汰的原则分配食物。狼群算法基于上述狼群捕食行为而提出,该算法的基本原理和步骤如下[6,8]。

步骤1 初始化。设在D维搜索空间中,由N匹狼组成一个人工狼群,其位置表示为

(1)

每匹人工狼的初始位置可通过式(2)随机生成：

(2)

式中:rand(0,1)为[0,1]区间上均匀分布的随机数;xdmin、xdmax分别为第d(d=1,2,…,D)维搜索子空间的下限和上限。

步骤2 游猎竞争领导者狼。狼群选派L匹最为精壮的狼(目标函数值好、位置优先)作为竞选狼,竞选狼在自己的周围按式(3)随机选取h个点进行游猎搜索,如果游猎搜索到的位置优于当前位置,则竞选狼进行移动,否则不移动。当竞选狼游猎搜索次数达到最大搜索次数hmax或竞选狼搜索到的位置得不到改善时,停止本轮搜索,选取当前位置最佳的竞选狼作为当前领导者狼。第i匹竞选狼进行游猎搜索产生的h个点的位置中第j(j=1,2,…,h)个点第d维的位置yijd为

(3)

式中:rand(-1,1)为[-1,1]内均匀分布的随机数;yid为第i只竞选狼第d维的当前位置;ad为第d维的搜索步长。

步骤3 领导者狼召唤奔袭。当前领导者狼通过嚎叫召唤同伴向它奔袭,按式(4)进行位置更新。若第i匹狼奔袭后的位置优于当前位置,则移动到当前位置,否则保持位置不变。

(4)

式中:zid为第i匹狼在第d维更新后的位置;xid为第i匹狼在第d维的当前位置；bd为第d维的奔袭步长；xld为领导者狼在第d维的位置。

步骤4 围攻猎物。领导者狼搜索到猎物,其他狼听从领导者狼召唤奔袭后,以领导者所在位置展开对猎物的围攻。围攻算法如下[8]:

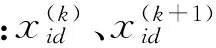
(6)

式中:kmax为最大迭代次数;cdmax和cdmin分别为第d维的最大、最小包围步长。按式(5)计算的位置有可能不在搜索空间内,应进行越界限制处理[8]。

本文对文献[8]的包围算法进行改进如下:当rand(0,1)>θ时,人工狼以领导者狼为中心对猎物进行围攻,只有当更新后的位置优于原来位置时才进行位置移动,否则保持位置不变;当rand(0,1)≤θ时,保持位置不变。

步骤5 狼群竞争更新。根据优胜劣汰原则,目标函数值好、位置优先的精壮的狼优先得到食物,导致部分弱小的狼会被饿死。随机生成m匹人工狼替代m匹目标函数和位置最差的人工狼更新狼群。

在以上步骤中,步骤2是精细搜索,体现了局部最优解的搜索精度,即尽可能不漏掉竞选狼周围的局部最优解;步骤3是粗糙搜索,体现了局部最优解的搜索效率;步骤4是逐步精细搜索,体现了收敛到局部最优解最终也是全局最优解的精度;步骤5得到的新一代狼群既保留了原狼群搜索到的局部最优点的优良性,又随机生成m匹人工狼替代m匹最差的人工狼,增加了搜索达到最优解的可能性,保证了算法的全局最优性。

2 优化调度问题的求解

考虑具有年调节性能的水电站水库优化调度问题。已知扣除水库水量损失和上游灌溉等用水后的各月净入库流量,在考虑水量平衡、水位约束、下泄流量约束、出力约束等条件下,合理安排各月的发电流量使水电站发电量最大。该问题的数学模型如下:

(7)

(8)

(9)

(10)

水量平衡约束

(11)

(12)

式中:Ei为第i时段的发电量;Vi-1、Vi分别为第i-1、第i时段初水库蓄水量;Qi为第i时段的平均入库流量;Hi为第i时段的平均水头;Δti为第i时段的时段长;K为综合出力系数;Zi为第i时段末水库蓄水位;Zimin、Zimax分别为第i时段的允许最低水位、最高水位;qi为第i时段的发电流量;qimin、qimax分别为第i时段要求的最小发电流量、允许最大发电流量;Ni为第i时段的平均出力;Nimin、Nimax分别为第i时段的最小允许出力(一般为保证出力)、最大允许出力(一般为装机容量或预想出力);di为第i时段的弃水流量。

为方便狼群算法优化求解,选择各时段末的水库蓄水位Zi(i=1,2,…,D)作为决策变量,采用罚函数来处理约束条件,将模型转换成无约束优化问题。将流量、出力约束处理为

式中:Φiq为第i时段发电流量约束的罚函数;ΦiN为第i时段出力约束的罚函数。

定义罚函数

(15)

式中:Φi为第i时段的罚函数;α为罚系数;β为平衡量级系数。

定义适应度函数

(16)

求解水电站水库优化调度狼群算法步骤如下:

步骤1 狼群初始化。将各时段末的水库蓄水位Z1、Z2、…、ZD看成D维决策空间中人工狼的位置x1、x2、…、xD,在水位允许变化范围内,随机初始化狼的位置。确定狼群算法参数,包括狼群中狼的个数N、最大迭代次数kmax、竞选狼的个数L、游猎搜索点数h、游猎最大搜索次数hmax、游猎搜索步长ad、奔袭步长bd、最大和最小包围步长cdmax和cdmin、围攻算法阈值参数θ、每次淘汰的最差狼的个数m。本文描述的水库优化调度问题中人工狼的位置X=(x1,x2,…,xD)的各分量均为库水位,具有相同的量纲和变幅,因此,游猎搜索步长、奔袭步长、最大和最小包围步长的各分量取相同值。对N匹狼的位置按式(2)进行初始化。

步骤2 游猎竞争领导者狼。按式(16)计算N匹狼的适应度函数,选择适应度函数值较大的L匹人工狼作为竞选狼,通过式(3)进行游猎精细搜索,按适应度函数值极大化原则确定领导者狼。

步骤3 领导者狼召唤奔袭。其他人工狼按式(4)进行粗糙的奔袭搜索,向具有当前最大适应度函数值的领导者狼位置移动。

步骤4 围攻猎物。其他狼听从领导者狼召唤奔袭后,以领导者所在位置按照式(5)的改进,展开对猎物的围攻计算。

步骤5 按照优胜劣汰的原则分配食物,除去狼群中适应度函数值最差的m匹狼,并在水位允许范围内按式(2)随机生成m匹人工狼。

步骤6 判断是否满足终止条件,若满足,则终止迭代,输出最优解;否则令k=k+1,返回步骤2,继续迭代直至满足结束条件。对于发电优化调度问题,建议的终止条件如下:

(17)

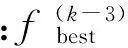
3 算例分析

3.1 问题简述

某年调节综合利用水库以灌溉、发电为主,兼有防洪、航运、渔业等综合效益。水库正常蓄水位160 m,死水位136 m,5月初至8月底为汛期,汛限水位 155 m。水电站设计保证率为95%,保证出力为12.5万kW,装机容量为32万kW,综合出力系数为8.5。计算各月发电流量,以使整个调度期发电量最大。

3.2 参数敏感性分析

文献[6,8]对狼群算法的参数选择进行了研究,但是否适用于水电站水库优化调度需要进一步的检验。

奔袭步长bd反映人工狼之间的信息共享和相互合作的情况,用于调整社会经验所起的作用大小,对优化性能有重要影响。本文主要对敏感参数即奔袭步长bd进行试算分析,其他参数设置同文献[8]:N=200、L=5、h=4、m=5、hmax=15、ad=1.5、cdmax=105、cdmin=0.5、θ=0.2。在试算中,奔袭步长bd的试算节点分别为0.1、0.5、0.9、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0。对每个试算节点独立运行求解20次,算法的评价指标最优值、平均值、标准差如表1所示。

表1 奔袭步长敏感性分析试算结果

由表1可以看出奔袭步长对算法的性能有一定的影响,奔袭步长在1.5～2.5时,无论是最优值、平均值还是标准差都很好,取得了令人满意的效果。

3.3 算法比较

为了进一步探讨狼群算法的性能,将本文改进后的狼群算法(IWPS)与原狼群算法[8](LWPS)、动态规划法(DP)、基本遗传算法(GA)及基本粒子群算法(PSO)通过本文算例进行比较分析。IWPS和LWPS的参数设置为:bd=2.0、N=200、L=5、h=4、m=5、hmax=15、a=1.5、cdmax=105、cdmin=0.5、θ=0.2。DP将水位分别离散成500点、1 000点。GA、PSO、LWPS、IWPS的初始化规模、迭代次数保持一致,分别为200、800。GA的参数设置为:选择概率Ps=0.7、交叉概率Pc=0.8、变异概率Pm=0.08。PSO的参数设置为:最大惯性权重wmax=0.9、最小惯性权重wmin=0.4、学习因子C1=C2=2.0。各种算法计算结果见表2,改进后的狼群算法最优调度过程计算结果见表3,其他算法最优调度过程计算结果略。

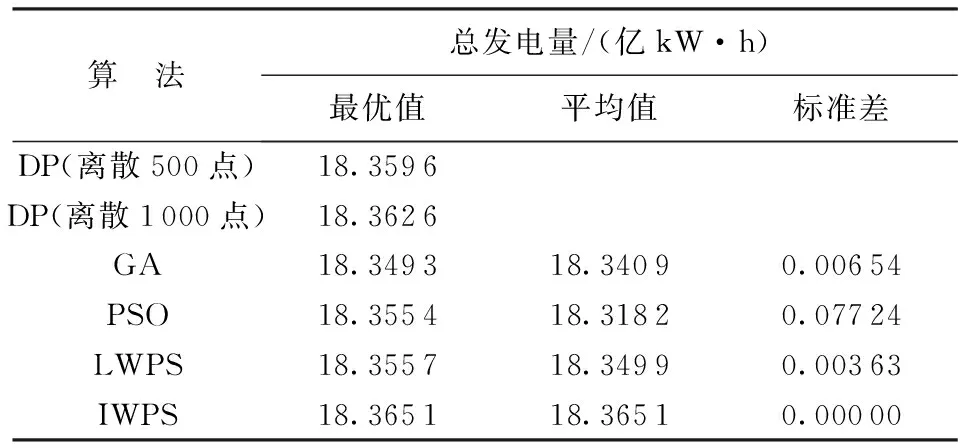
表2 各算法计算结果比较

从表2可以看出:在几种优化方法中,改进后的狼群算法无论是最优值、平均值还是标准差均最优。改进后的狼群算法计算结果优于动态规划法,这主要是由于改进后的狼群算法不需要离散决策变量,而动态规划法需要离散决策变量,计算精度与离散点数有关,离散点数越多计算精度越高。两种狼群算法即原狼群算法和改进后的狼群算法均优于基本遗传算法和基本粒子群算法。改进后的狼群算法计算结果优于原狼群算法,表明本文对围攻算法的改进是有效的。

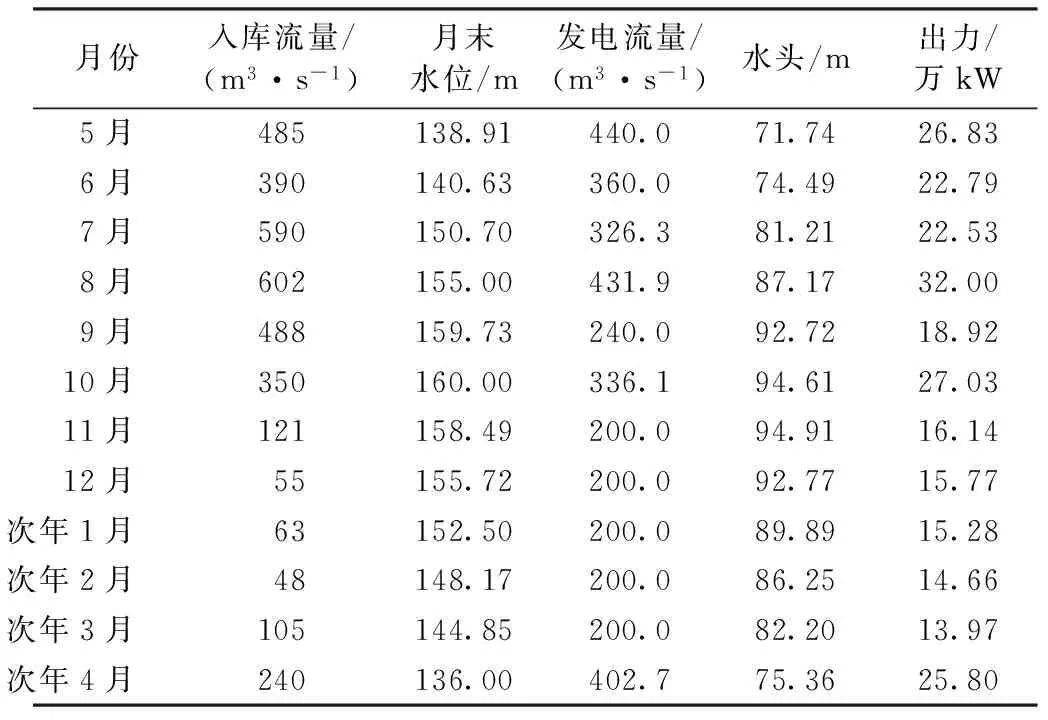
表3 IWPS最优调度过程计算结果

4 结 语

本文对一种新的群体智能算法——狼群算法及其在水电站水库优化调度中的应用进行了研究，改进了狼群算法中的围攻算法,给出了水电站水库优化调度问题的狼群算法设计及求解步骤。结合某水电站水库优化调度实例,对狼群算法的敏感参数奔袭步长进行了模拟计算和敏感性分析,给出了奔袭步长的有效取值范围。计算分析结果表明,改进后的狼群算法及原狼群算法均优于动态规划法、基本遗传算法及基本粒子群算法,且改进后的狼群算法优于原狼群算法。

本文仅对狼群算法的奔袭步长进行了模拟计算和敏感性分析,狼群算法的狼群规模、游猎搜索狼的个数、游猎搜索步长、围攻算法阈值等参数的取值还有待进一步的分析研究。

[ 1 ] HOLLAND J H.Adaptation in natural and artificial systems [M].Ann Arbor:University of Michigan Press,1975.

[ 2 ] DIROGO M,MANIEZZO V,COLORNI A.Ant system:optimization by a colony of cooperrting agents [J].IEEE Trans on SMC,1996,26(1):28-41.

[ 3 ] KENNEDY J,EBERHART R C.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks.Perth:[s.n.],1995:1942-1948.

[ 4 ] 张伟,李守智,高峰,等.几种智能最优化算法的比较研究[C]//第二十四届中国控制会议论文集(下册).广州:中国自动化学会，2005：1316-1320.

[ 5 ] YANG Chenguang,TU Xuyan,CHEN Jie.Algorithm of marriage in honey bees optimization based on the wolf pack search[C]//Proceedings of IEEE Computer Society International Conference on Intelligent Pervasive Computing.Jeju Island：[s.n.],2007:462-467.

[ 6 ] LIU Changan,YAN Xiaohu,LIN Chunyang,et al.The wolf colony algorithm and its application[J].Chinese Journal of Electronics,2011,20(2):212-216.

[ 7 ] TANG Rui,SIMON Fong,XIN Sheyang,et al.Wolf search algorithm with ephemeral memory[C]//Proceedings of IEEE Digital Information Management (ICDIM) Seventh International Conference.Macau：[s.n.],2012:165-172.

[ 8 ] 周强,周永权.一种基于领导者策略的狼群搜索算法[J].计算机应用研究,2013,30(9):2629-2632.(ZHOU Qiang,ZHOU Yongquan.Wolf colony search algorithm based on leader strategy[J].Application Research of Computers,2013,30(9):2629-2632.(in Chinese))

[ 9 ] LI Chienming,DU Yichun,WU Jianxing,et al.Synchronizing chaotification with support vector machine and wolf pack search algorithm for estimation of peripheral vascular occlusion in diabetes mellitus[J].Biomedical Signal Processing and Control,2014,9:45-55.

[10] 董子敖.水库群调度与规划的优化理论和应用[M].济南:山东科技出版社,1989:113-134.

[11] HARBOE R.Multi-objective decision making techniques for reservoir operation[J].Water Resources Bulletin,1992,28(1):103-110.

[12] 钟平安,唐林.水库优化调度遗传算法参数的灵敏性分析[J].水力发电,2012,36(11):13-16.(ZHONG Pingan,TANG Lin.Synchronizing chaotification with support vector machine and wolf pack search algorithm for estimation of peripheral vascular occlusion in diabetes mellitus[J].Water Power,2012,36(11):13-16.(in Chinese))

[13] 张双虎,黄强,吴洪寿,等.水电站水库优化调度的改进粒子群算法[J].水力发电学报,2007,26(1):1-5.(ZHANG Shuanghu,HUANG Qiang,WU Hongtao,et al.A modified particle swarm optimizer for optimal operation of hydropower station[J].Journal of Hydroelectric engineering,2007,26(1):1-5.(in Chinese))

Application of wolf pack search algorithm to optimal operation of hydropower station//

WANG Jianqun, JIA Yangyang, XIAO Qingyuan

(CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China)

In order to explore a new method for solving the problem of optimal operation of hydropower station, a new swarm intelligent optimization algorithm, i.e., wolf pack search algorithm, and its application to optimal operation of hydropower station were studied. The siege algorithm of the wolf pack search algorithm was improved. Design and solving steps of the wolf pack search algorithm for solving the problem in optimal operation of hydropower station were proposed. Based on the simulation test and analysis of the example of optimal operation of hydropower station, the effective range of the step on the raid of the wolf pack search algorithm was proposed. Simulation results show that the wolf pack search algorithm is new effective method for optimizing the operation of hydropower station.

wolf pack search algorithm; swarm intelligent algorithm; hydropower station; reservoir optimal operation

水利部公益性行业科研专项(201101011)

王建群(1960—),男,江苏句容人,教授,博士，主要从事水资源规划和管理研究。E-mail:wangjq@hhu.edu.cn

10.3880/j.issn.1006-7647.2015.03.001

TV737

A

1006-7647(2015)03-0001-04

2014-02-16 编辑：骆超)