高等数学数形结合教学法的研究与实践
——以山东建筑大学为例
王爽,李秀珍,赵永谦,孙亚楠(.山东建筑大学理学院,山东济南 500;.山东医学高等专科学校,山东济南 5000)
高等数学数形结合教学法的研究与实践
——以山东建筑大学为例
王爽1,李秀珍1,赵永谦1,孙亚楠2
(1.山东建筑大学理学院,山东济南250101;2.山东医学高等专科学校,山东济南250002)
高等数学是工科院校学生的重要基础理论课,运用数形结合教学法可以将抽象的概念直观化,提高学生的积极性和学习效率。文章结合山东建筑大学高等数学教学,分析了教学过程中几何教学法存在的问题和数形结合的重要性,提出了可以用于教学实践的数形结合教学方法,采用启发式教学法与几何教学法相结合的手段,通过分析图像提出问题引导学生学习,并在山东建筑大学高等数学教学中取得了一定的成绩。
高等数学;数形结合;直观性;抽象概念;动态图像
0 引言
高等数学是一门重要的基础理论课,其教学效果直接影响工科类专业的本科教学质量以及创新人才的培养。高等数学的内容严谨,高度逻辑性的分析语言体现了数学之美,但是抽象的数学概念也造成了学生理解上的困难,如何改进高等数学的教学过程一直是教学研究的重要课题。2015年教师节前夕,李克强总理提出希望教师做精做细教学本职激发和挖掘学生的创新能力。在教学手段日益丰富的今天,教师应该思考适应时代要求、适于学生学习的教学方法,培养学生的数学思维,激发学生的创新能力。
随着多媒体课件以及数学软件的兴起,几何教学法近年来越来越受到重视[1]。几何图像可以将抽象的高等数学概念具体化,使学生通过形象思维直观地理解概念,但是单纯应用几何图像教学往往具有具体性的特征,无法展示数学的逻辑性。已有文献多是对几何图像进行举例展示,较少涉及对几何图像的引入分析[2-3]。如果教师在几何教学的过程中通过提问、对比等方式启发学生思考,使学生能够用代数语言描述几何问题,或者用几何图像分析代数问题,那么对于培养学生的创造力和解决问题的能力都有重要意义。
文章结合山东建筑大学数学教学,分析了教学过程中几何教学法存在的问题和数形结合的重要性,将启发式教学法[4]与几何教学法相结合,通过分类举例详细说明数形结合教学法在高等数学中的应用,在对教学内容进行几何展示的同时,分析几何图像并提出问题,引导学生用数学思维去观察、解决问题。
1 高等数学教学中几何教学法存在的问题
1.1教学学时不足和资源有限
高等数学是工科类专业学生学习后续技能的必备课程,例如大学物理、力学、电学等课程都用到了高等数学的知识,机械设计课程与定积分的几何应用密切相关。但是高等数学课程教学学时不足,教师只能将教学内容进行压缩,删减复杂的定理证明,忽视引导学生从问题来源和几何直观化方面理解概念定理,缺少必要的几何应用训练教学[5]。普通工科院校的另一现状是教学资源有限,以山东建筑大学为例,高等数学采用大班授课,学生过多导致教师无法兼顾每一个学生的学习特点和学习进度,不能采用以学生讨论为主的教学方法,学生被动地接受知识,缺乏独立思考和创新思维的能力。
1.2教学方法单一
学生对课程的关注度主要由学生的学习热情和积极性决定,几何教学法可以将数学的美和神奇展现出来,使学生在生动活跃的学习环境中培养对数学的兴趣。但是教师过分强调几何图像的展示,缺少对数学思想的阐述,或者以几何图像代替对定理概念的理论证明,使得学生对问题的认识仅能停留在感性阶段,难以上升到理性阶段[8]。建筑工程中存在着大量的几何问题,而高等数学的定理概念都是用代数语言去描述的,如果学生不知道代数理论与几何现象之间的联系,那么面对工程问题时就难以应用所学的数学知识解决实际问题。
1.3教学应用存在误区
借助于现代教具,教师可以通过数学软件的作图能力构造生动准确的几何图像,解决板书教学时难以处理的作图问题[6-7]。但是教师在做几何展示的过程中容易产生以偏概全的假象,学生会错误地认为通过构造特殊函数的几何图像可以代替应用严格的分析语言证明定理。事实上采用几何图像演示教学内容在本质上说是通过举例的方法进行授课列举法不能涵盖所有的情况,因此在教学时需要慎重选择几何示例,并说明举例的特殊性,必要时可以选取多个几何示例作对照。
2 高等数学数形结合教学法的重要性
分析高等数学的内容和方法会发现,研究几何问题是微积分的重要起源,也渗透于高等数学的每一个章节[9]。有些直观的几何现象用抽象的数学分析语言描述出来就是高等数学中的概念定理。应用几何图像可以直观地理解抽象概念[10]、寻找证明思路、化简积分的计算[11-12],化难为易。
数形结合的过程既是将抽象的数学语言与直观的图形相结合,实现抽象概念与形象表现之间转化的过程,也是学生的形象思维与抽象思维共同运用互相促进的过程,学生通过形象思维理解数学概念可以提高学习积极性和学习效率。因此可以应用数形结合的方法启迪学生思考、激发学生兴趣。
我国古代从宋元时期就形成了数形结合的思想,通过用代数语言描述一些几何现象,将几何关系的研究归结为函数表达式之间的代数关系,成为解析几何的先驱。因此教师在高等数学教学中加强培养学生的兴趣和应用数学知识解决问题的能力有很重要的实际意义。
3 高等数学数形结合教学改革方法
针对高等数学教学中几何教学法存在的问题考虑到工科院校教学学时不足、教学资源有限的现状一时难以改变,提出如下改革方法:
3.1重视对数学思维的阐述
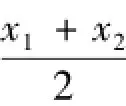
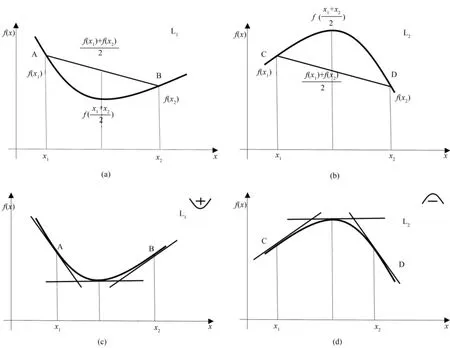
图1 曲线凹凸性示意图
由图像得到了凹凸性的定义,进一步地通过图像总结出判定定理。为得到凹凸性和导数之间的关系,根据导数的几何意义,可以过曲线上自变量依次递增的三个点做切线,让学生观察这三点处曲线的切线倾斜程度。学生对比发现图1(c)中凹弧的切线倾角随着自变量的增大而增大,即一阶导数单调递增,如果函数二阶导数存在,那么二阶导数大于0。而图1(d)中凸弧恰好相反,切线倾角随着自变量的增大而减小,即一阶导数单调递减,二阶导数小于0。得到了凹凸性的判定定理后,再结合图像加以证明。最后,为避免学生混淆凹凸性与二阶导数的关系,可以通过图1(c)和图1(d)中右上角的符号帮助学生加深记忆,凹弧二阶导数符号为正,凸弧二阶导数符号为负。
再比如,在学习一元函数与极限中无穷大的概念时,学生经常将无穷大与无界函数的概念相混淆无穷大的定义为[13]:如果对于任意给定的正数M总存在正数δ(或正数X),只要0<|x-x0|<δ(或|x|>X)时,函数f(x)的绝对值都大于M,那么称f(x)为当x→x0(或x→∞)时的无穷大。而无界函数的定义为[13]:如果对于任意给定的正数M,总存在f(x)的定义域内的一点x0,使得函数f(x)的绝对值大于M,那么称f(x)在定义域内是无界函数。从数学分析语言上学生难以理解和区分这两个概念,此时可以借助几何图像举例说明。例如:函数y=e是当x→+∞时的无穷大,其图像如图2(a)所示当x→+∞时,函数值逐渐增大,函数曲线向y轴的正无穷方向延伸,通过在y轴上任意选取y=M,总可以对应地找到x0=X,使得|x|>X时,|ex|>M。
图2 无穷大与无界函数对比图示意图
与之相对应地,无界函数y=xcosx不是当x→+∞ 时的无穷大[14],其图像如图2(b)所示,当x→+∞时,函数值的振荡幅度虽然逐渐增大,并趋向于y轴的正负无穷方向,但是函数值始终会回落到y=0附近,此时任意选取y=M,当x→+∞时,不仅存在使|f(x)|>M的点,也存在使|f(x)|≤M的点x1,即当x→+∞时函数f(x)的绝对值并不一致趋于+∞。
以上的教学实例都是结合抽象概念的几何图形,通过对比图形加深学生对概念的理解。教师不仅借助几何意义解释概念定理,更注重引导学生用数学语言描述现实中的几何现象,使学生理解数学是描述现实世界的工具,认识数学的重要性。
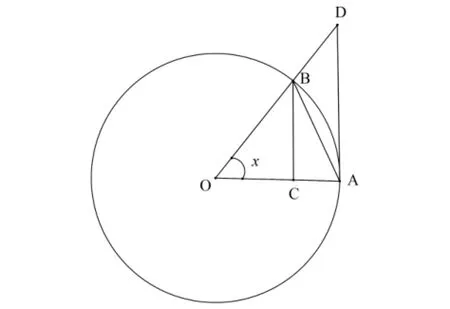
图3 四分之一的单位圆示意图
3.2应用几何图像启发学生思考
又如中值定理是用分析语言描述连续曲线在闭区间上的几何现象,因为曲线方程由抽象函数表示,所以证明定理存在困难。在讲解拉格朗日中值定理时,教师先对比了图4中的(a)和(b):观察图4(a)满足罗尔定理的情况可以发现,如果一条连续的曲线弧,除端点外处处有不垂直于x轴的切线,且过两个端点的弦AB平行于x轴,那么必在AB间存在最高点C,过C点的切线平行于x轴,也即平行于弦AB,切线斜率为0。将图4(a)中的弦AB以A为中心旋转任意角度就得到图4(b),曲线端点A、B不再有高度相等的限制,但过点C的切线平行于弦AB的性质仍然成立,因此过点C的切线斜率等于弦AB的斜率。
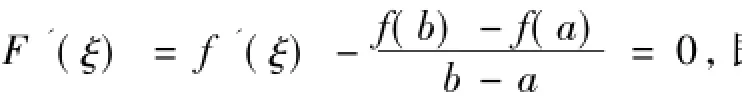

图4 中值定理的几何意义示意图
以上的教学实例说明,结合几何图形可以改变以往对证明过程繁琐沉闷的讲解方法,开拓学生的思路,帮助学生形成数学思维,活跃课堂氛围,但是不能避繁就简,代替定理在理论上的证明过程。
3.3合理选取几何示例充实教学内容
除了一些从几何空间中抽象出的数学概念外,还有一些表面上并不具有几何直观意义的数学概念可以通过几何图像加深理解。例如,在学习无穷级数这一概念时,学生难以理解为什么需要将函数表达成无穷级数,因此难以对无穷级数的相关理论产生兴趣。采用几何图像演示的方法可以使学生看到简单函数的图像是如何逐渐接近于复杂函数图像的,继而了解用简单函数构成的无穷级数来表达复杂函数是刻画复杂函数的有效方法。

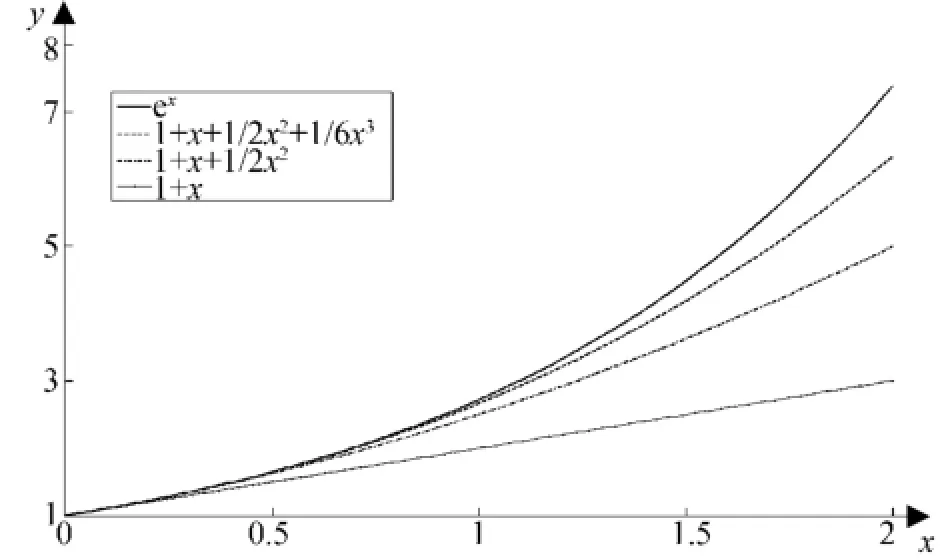
图5 幂级数部分和逼近ex的示意图


图6 傅里叶级数部分和形成的波形图
4 应用数形结合教学法取得的成效
我校高等数学教学团队在深入挖掘教学内容的基础上,对每个知识点都找到相应的几何意义,并对教学时所展示的几何图像补充相应的问题和说明分析,使得教学内容不仅呈现出数学的美,更加体现出数学的逻辑思维。在工学及物理类专业的高等数学教学中应用了数形结合方法后,在课时量不变的情况下,增加了师生间的互动,例如讲解微分中值定理时,以往的教学过程主要以教师讲解为主,现在教师结合图像可以提出两到三个启发性的问题,学生通过发现总结等主体思维过程主导定理的推导过程成为课堂的主人,最终学生对三个中值定理之间的关系更加明确。
借助山东建筑大学课程教学质量学生评分体系,对应用数形结合方法前后各两个学年的得分情况进行对比,发现学生对以下五个指标的测评满意度明显增高:“教师能有效利用实例授课”、“注重思维能力培养及启发式教学”,“备课充分,多媒体课件制作精良效果好”“授课内容易于接受和掌握,学生的知识和能力得以提高”“课堂教学气氛活跃,教学效果得以保证”。通过对材料学院成型焊接两个专业学生的调研发现,学生的出勤率增加了,课后提问的学生人数也增加了,说明学生的学习主动性得以提高。
需要说明的是,在讲解时应用数形结合常常会给学生一种以偏概全的假象,学生会错误地认为通过构造特殊函数的几何图像可以代替应用严格的分析语言证明定理。事实上采用几何图像演示教学内容在本质上说是通过举例的方法进行授课,列举法不能涵盖所有的情况,因此在教学时需要慎重选择几何示例,并说明举例的特殊性,必要时可以选取多个几何示例作对照。
5 结语
文章分析了高等数学教学中存在的问题,提出了以培养学生数学思维、创新能力为最终目的的数形结合教学法,并针对教学过程中所发现的学生难以理解的知识点为例,给出了可以用于实践的数形结合教学方法。文章所举实例从多个方面说明了数形结合不仅可以生动地展现高等数学的教学内容还可以将抽象概念直观化、开拓学生思路、拓展学生想象力,在活跃课堂氛围、增加学生学习兴趣的同时,培养学生分析问题解决问题的能力。
[1]Timothy P.,Charlene N..Analyzing the teaching of advanced mathematics coursesviatheenactedexamplespace[J]. Educational Studies in Mathematics,2014,87(3):323-349.
[2]Ghislaine G.,Luc T..Mathematics teacher education advanced methods:an example in dynamic geometry[J].Mathematics Education.2011,43(3):399-411.
[3]李志明,李宏伟.例说加强高等数学课程中的几何教学[J].大学数学,2013,29(3):136-138.
[4]葛倩,李秀珍.高等数学研究性教学方案探析[J].山东建筑大学学报,2013,28(1):82-85.
[5]袁玉波,曹飞龙.基于几何直观的微积分教学内容改革探索[J].大学数学,2010,26(1):102-104.
[6]王俭侠,龚力强.Maple在高等数学教学中的应用[J].广州大学学报(自然科学版),2002(6):67-73.
[7]张颖,吴建华.高等数学多媒体辅助教学的实践与思考[J].高等数学研究,2006,9(4):110-112.
[8]薛洪.高等数学教学中的直观教学[J].大学时代,200 (11):114-115.
[9]高永良,王燕燕.几何学在高等数学教育中的作用[J].开封大学学报,2010(8):76-77.
[10]赵小艳,李换琴.借助几何图形理解高等数学中的抽象概念和结论[J].大学数学,2014,30(1):84-87.
[11]李长青.高等数学教学中应重视几何直观的作用[J].高等数学研究,2007,10(2):25-27.
[12]程新跃,刘祥伟.关于高等数学课程中几何教学的认识与实践[J].高等数学研究,2006,9(3):11-13.
[13]同济大学数学系.高等数学(第6版)[M].北京:高等教育出版社,2007.
[14]李秀珍,隋梅真.高等数学全程学习指导[M].北京:北京邮电大学出版社,2011.
[15]菅小艳.MATLAB在高等数学中的应用[J].计算机时代2011(5):51-53.
(学科责编:王光银)
Application of geometric interpretation in the advanced mathematics teaching
Wang Shuang,Li Xiuzhen,Zhao Yongqian,et al.
(School of Science,Shandong Jianzhu University,Jinan 250101,China)
Advanced mathematics is an important foundation of the whole university learning for engineering college students.The geometric interpretation method can be beneficial to illustrate the abstract concepts and stimulate the students'interest.According to the actual experience of higher mathematics teaching in Shandong Jianzhu University,this paper analyzes the problems of geometry teaching method and the importance of combining abstract mathematical conclusions with geometry. Then,the geometric interpretation method is proposed which combines heuristic teaching method and geometry teaching method.Through asking appropriate questions and the analysis of images,teachers guide the students'learning process and have made some achievements in higher mathematics teaching of Shandong Jianzhu University.
advanced mathematics;geometric representations;visibility;abstract concepts;dynamic image
O13-4;G642
A
1673-7644(2015)06-0600-07
2015-07-06
山东省高等学校教学改革研究项目(2009262);山东省高等学校教学改革研究项目(2012298);山东建筑大学博士科研基金(XNBS1338)
王爽(1984-),女,讲师,博士,主要从事数学教学和科学计算等研究.E-mail:persever1019@163.com

