航天器相对视觉/IMU导航量测修正多速率滤波

曾占魁，曹喜滨，张世杰，华 冰，吴云华

(1.哈尔滨工业大学卫星技术研究所，150008哈尔滨;2.南京航空航天大学微小卫星工程技术研究中心，210016南京)

微小卫星编队已成为美国空军实验室以及NASA宇航局众多在研空间科学任务如电子侦查、立体成像、光学干涉等任务的关键技术之一［1］，也是实现空间攻防的有效手段，受到国内外航天机构的普遍关注.编队卫星协同工作能满足多种未来航天任务需求［1-4］.相对状态确定是卫星编队的关键技术之一，同时也是卫星编队的基本前提.相对轨道与姿态估计方法有基于差分GPS及类GPS的测量方法，前者为半自主式测量方法，受GPS信号覆盖范围影响仅适用于LEO轨道编队［5］.后者由于无线电接收天线相对距离较近，存在多路径效应的缺陷［6］.鉴于上述方法的不足，美国德克萨斯A＆M大学研制了视觉相对测量敏感器，通过特征点在焦平面上的投影坐标获取特征点方向矢量，此方法能够提供较为精确的相对状态测量［7-10］.

单目视觉导航常用于合作航天器，例如在航天器交会对接阶段，可事先设置特殊构型的特征点系统，因此可以保证在交会对接期间的相对位姿始终满足视觉测量条件.针对交会对接的绕飞阶段，可以在追踪航天器上布设2～3个视觉相机，同时对追踪/目标航天器进行姿态控制，可以保证目标航天器一直在追踪航天器的视场内;针对交会对接的逼近阶段，由于双方相对姿态保持稳定，因此可以一直保证目标航天器的可观测性.但限于视觉相机的作用距离，该方法适用于近距离编队飞行的相对导航.随着距离的增大，视觉导航精度会严重下降.

由此可见，基于单目视觉的相对导航能够满足多种航天任务的相对状态测量需求，但由于视觉敏感器的尺寸和象元限制，以及图像处理计算量大等特点，使其有效测量距离较短且测量频率低.惯导(IMU)是航天器导航的首选配置，其可靠性高，属于全自主导航，短期精度好，能够以较高的频率提供位置、速度和姿态等信息，但其误差随时间逐渐变大.本文针对视觉和IMU系统的各自优缺点，有机地将两种系统组合起来，针对近距离航天器编队研究采用单目视觉/IMU组合的相对导航方法，提高组合导航系统的相对状态估计性能和可靠性.针对视觉导航系统与惯导系统输出频率不同造成的异速问题，以及由于视觉敏感元件自身特性而造成的视觉系统量测噪声不确定的特点，本文提出基于量测修正的视觉/IMU多速率卡尔曼算法，以提高滤波器性能，并通过数学仿真验证其有效性.

1 问题描述

1.1 坐标系定义

首先给出相关坐标系定义:

1)地心惯性坐标系OXIYIZI:其坐标原点位于地心O，XIYI平面位于赤道平面内，XI轴指向春分点Υ，ZI轴指向北极与地球自转轴重合.

2)相对运动参考坐标系oxyz:目标航天器的质心为坐标原点o，x轴由地心指向目标星，z轴方向为轨道角动量方向.相对运动参考坐标系又被称为Hill坐标系，用r表示.

3)体坐标系:原点定义在卫星质心OC处，XC轴指向主轴方向，YC轴在垂直于主轴的横截面内.

需要指出的是本文所用坐标系均为右手坐标系.

1.2 相对运动模型

记为向量s在坐标系N中的时间导数，sN为s在坐标系N中的分量形式.

目标航天器和追踪航天器的轨道动力学方程分别为

其中rc和rd分别为目标和追踪航天器在惯性坐标系中的位置.

则追踪航天器相对目标航天器的位置为

其二阶导数为

式(1)在相对运动坐标系中可表示为

式中ωo为目标航天器的轨道角速度矢量，在相对运动坐标系中有ωo=［0，0，］T.

略去下标，并假设星间距离远小于目标航天器的地心距，上式可简化为

式中rc为目标航天器的地心距，θ为目标航天器的真近点角.

追踪航天器体坐标系相对于Hill坐标系的相对姿态采用四元数q=［q1，q2，q3，q4］T来描述，则相对姿态运动学方程为

式中ω=［ω1，ω2，ω3］T是追踪航天器体坐标系相对于Hill坐标系的角速度，有

式中ωd是追踪航天器的惯性角速度.

在惯性系中求导，有

可进一步描述为

对于追踪航天器，其姿态动力学方程可表示为

式中Jd是追踪航天器的惯量矩阵，Td是所受外部力矩.

经整理可得

则追踪航天器相对目标航天器的姿态动力学方程为

1.3 组合导航方案

视觉/惯性组合相对导航方案如图1所示［11］.假设陀螺和加速度计采用正装方式安装，其测量即为追踪航天器体坐标系下的运动参数.陀螺输出的是追踪航天器相对惯性坐标系的姿态角速率在追踪航天器体坐标系中的分量，加速度计输出的是加速度在追踪航天器本体系中的比力投影.在近距离相对导航中可把目标航天器视为相对静止的目标，而追踪航天器进行逼近机动.以目标航天器体坐标系为惯性导航参考坐标系.惯性导航系统的加速度计和陀螺仪等惯性敏感器能够对航天器相对运动产生的加速度和角速度信息进行高速率测量，利用惯性导航算法估计出位置、速度、姿态角和角速度等多种相对状态.由于惯性敏感器自身的噪声漂移将导致系统会产生随时间累积的误差，因此本文采用单目视觉系统对惯导系统进行修正.单目视觉相机对目标航天器成像后经图像处理获取目标的特征信息，然后利用单目视觉导航算法解算出相对位姿.因视觉和惯导系统的采样周期不同，所以传统的单速率卡尔曼滤波理论不适用于本文提出的组合导航系统，因此本文提出一种多速率卡尔曼信息融合算法以解决组合系统更新速率不同的问题.

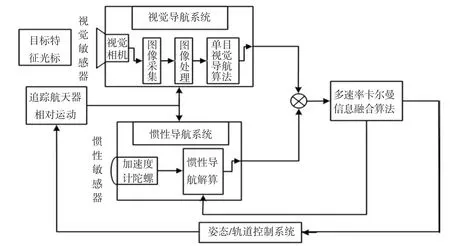
图1 视觉/惯性组合相对导航方案

2 多速率滤波算法

2.1 视觉/IMU组合导航系统模型

2.1.1 状态方程

组合导航系统状态量包括平台失准角误差、加速度误差、速度误差和位置误差，下面分别加以描述.

假设惯性导航系统IMU中陀螺仪的漂移速度与导航坐标系漂移速度相同，忽略加速度测量计误差中二阶以上小量，则加速度的测量误差方程有

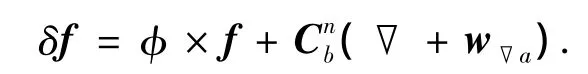
其分量形式为

式中:f表示加速度计测量的比力;φ表示平台失准角;▽表示加速度计偏置;w▽a表示加速度计白噪声;Cn

b表示从追踪航天器本体系到导航坐标系的姿态转移矩阵.

在导航坐标系中，追踪航天器的位置/速度误差方程为

式中:d14～d36为引力加速度对位置矢量的相对导数，此处假设为零;(x，y，z)为追踪航天器在导航坐标系下的坐标分离，可转换为追踪航天器在目标航天器体坐标系下的位置.

忽略陀螺误差的二阶及二阶以上小量，平台失准角的误差方程可表示为

其分量形式为

式中ε表示陀螺仪常值漂移，wε表示陀螺仪测量白噪声.

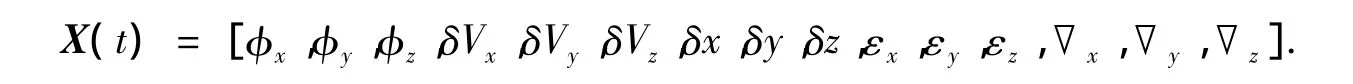
结合上述3个误差方程，则组合导航系统状态方程为等号右侧的5组分量分别为姿态误差角、速度误差、位置误差、陀螺漂移和加速度偏置.式(2)中F(t)是状态转移矩阵，G(t)和W(t)是系统噪声矩阵，分别有且W(t)满足

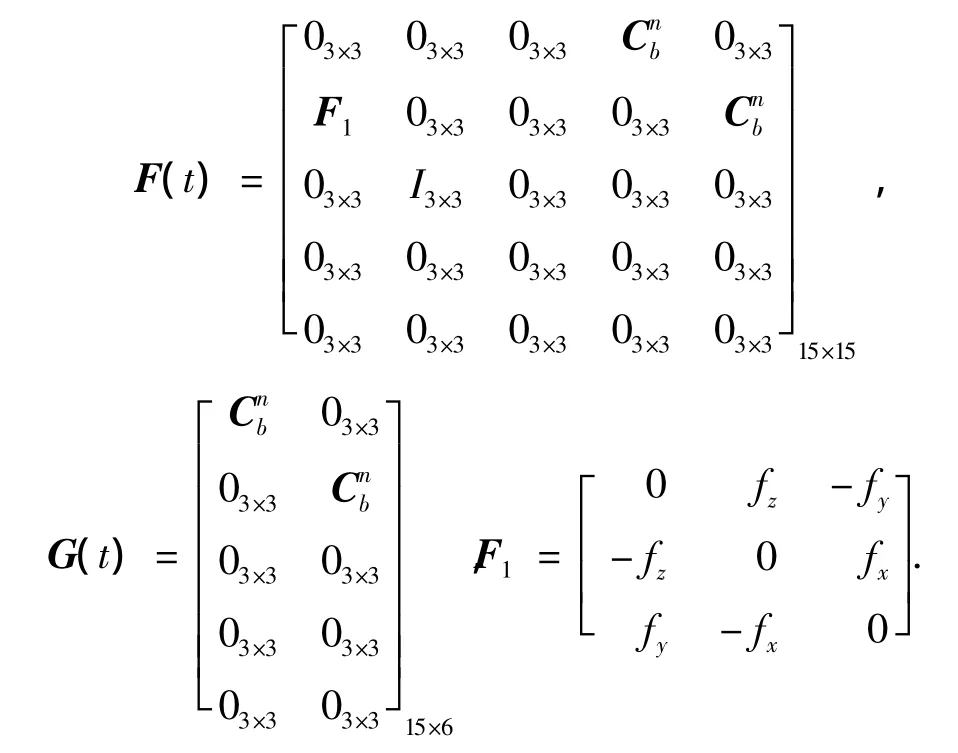
式中wεx，wεy，wεz表示陀螺随机漂移;w▽x，w▽y，w▽z表示加速度计随机偏置.

将状态方程离散化为

式中Φk+1·k为一步转移阵，可由下式计算:

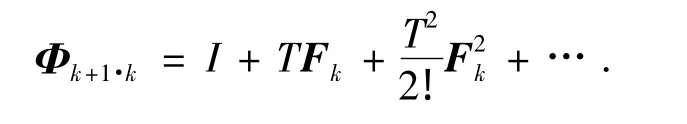
式中:T为滤波周期;Wk为系统噪声序列，满足:

Qk为系统噪声序列方差阵，为非负定阵，有Qk=

2.1.2 量测方程

假设单目视觉相机已经过标定，视觉导航的关键问题在于根据特征点在目标坐标系中和相机坐标系中的坐标来求解相对位姿参数.一般可采用迭代估计方法，依次对景深和相对位姿进行估计，在此基础上求解新的景深，不断迭代上述过程直至解趋于收敛.Haralick［11］提出了一种同时计算目标位置和景深的迭代算法，该方法采用特征值分解来求解相对位姿，本文也采用该算法对视觉导航数据进行仿真.

组合导航系统以惯性/视觉导航系统估计的相对位置和姿态的差值作为滤波器测量值.那么组合导航系统量测方程为

状态变量X(t)可表示为

且有

其中:下标INS表示惯导系统测量量;Vis表示视觉导航系统测量量;γ，φ和θ为三轴姿态角;x，y和z表示位置.Vk为量测噪声，满足高斯白噪声过程，即E［Vk］=0，cov［Vk，Vj］=E［VkVTj］=Rkδkj.同时，Vk和Wk还满足cov［Wk，Vj］=E［WkVTj］=0，Rk为系统噪声方差阵，且为正定阵.

2.2 多速率滤波建模

多速率卡尔曼信息融合算法的核心思想是:以导航子系统中最小滤波周期作为组合导航系统的滤波周期，从而提高状态更新率.组合导航系统的滤波周期可以分为时间更新和量测更新两个过程.当滤波时刻没有慢速率视觉测量值，滤波器仅进行时间更新;当滤波时刻出现慢速率视觉量测值，滤波器同时进行时间更新和量测更新［12-15］.

多速率卡尔曼信息融合滤波算法的优点:

1)滤波器能够始终以最快采样周期进行状态估计，使系统不再受采样周期不等的影响，提高了数据的更新率;

2)提高了数据利用率，有助于提高滤波性能;

3)由于在滤波时刻对有无慢速率视觉量测信息进行了判断，即使视觉导航采样周期不固定，或者在滤波时刻视觉导航采样点出现异常中断，滤波系统即认为没有出现视觉量测信息，继续进行滤波的时间更新.这样提高了系统冗余性，解决了传统集中式滤波器因某一子系统的量测更新失败就会造成滤波性能下降的问题.

组合导航滤波周期内的卡尔曼滤波器更新过程包含时间更新和量测更新.卡尔曼滤波迭代过程分为［14］:

1)时间更新.状态一步预测为

一步预测误差方差阵为

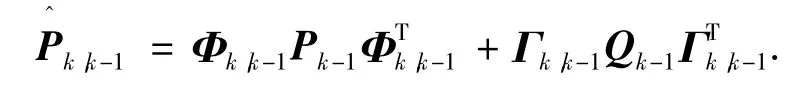
2)量测更新.滤波增益矩阵为

状态估计为

估计误差方差阵为

若没有测量信息输出，则滤波器仅进行时间更新;有量测信息输出时，卡尔曼滤波器则要进行正常的时间更新以及量测更新.

从原理上解释，在滤波时刻k时，如果缺少视觉导航的量测信息输入，那么滤波器认为系统出现了粗大误差，此时系统的观测噪声方差阵Rk会趋向于无穷大，然后滤波增益矩阵计算中的会趋向于零，滤波增益矩阵也趋近于零，则

表示量测更新过程没有起到作用，只进行时间更新过程.

记惯性导航解算周期为TINS，视觉导航解算周期为TVision，滤波周期为TFilter，且有

其中N和M均为正整数.

取N=1，M=2～3(视觉导航估计周期不固定).假设视觉导航估计周期和滤波周期均为惯性导航的整数倍，可认为每个采样点都有惯性导航的量测值.由于视觉导航采样频率慢，且输出周期并不恒定，当无视觉导航的量测信息的t1，t3，t4时刻，系统滤波增益趋近于零，滤波器仅进行时间更新;在有视觉导航量测信息的t0，t2，t5时刻，滤波器进行时间和量测更新，所有滤波方程都得到更新.可以看出，异速卡尔曼滤波器缩短了滤波周期，增加了对测量信息的判别，提高了数据使用率及系统的可靠性.

3 多速率滤波器的量测修正

本文设计的异速滤波只对导航量测信息的有无起到有效隔离作用，但对量测信号的质量却不加以控制，只做了最优假设.实际上，视觉与惯性测量信息均可能出现野值、故障、粗大误差等情况，若不控制的加以修正，会造成估计偏差.本节研究如何在多速率滤波的基础上对量测信号质量和滤波修正效果加以控制.

3.1 量测噪声阵的量测估计

在k时刻，系统的观测值Zk的预测估计值为

记k时刻观测值为Zk，它与预测值，k-1的差值k为

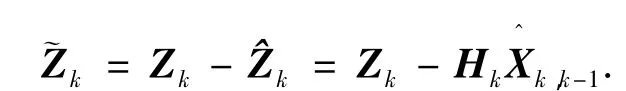
根据滤波理论:

记协方差阵为Bk，则

根据新息的n组历史数据，可以估算出新息协方差阵:

则量测噪声阵的估计值为

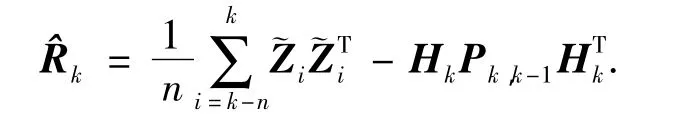
滤波量测噪声阵与量测噪声估计的差值为

则修正后的量测噪声估计阵为

为了避免量测数据长度不足、野值、故障、粗大误差等原因造成的估计偏离，量测修正采用一定的比例系数:

3.2 状态估计误差协方差阵估计

估计误差方差阵:

设X*

k为状态理想值，理想滤波误差协方差矩阵为

误差方差阵差值为

为了控制误修正的影响程度，状态估计误差协方差阵修正也采用一定的比例系数:

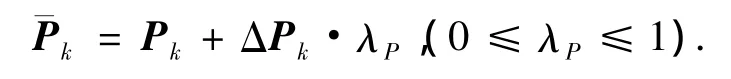
4 仿真与分析

滤波初值选取如下.相对姿态角误差为0.5°、0.5°、0.5°，相对位置误差为3 m、3 m、3 m;相对速度误差为 0.01 m/s、0.01 m/s、0.01 m/s;陀螺测量误差:常值漂移0.035°/h，随机漂移方差σ2=(0.035°/3h)2;加速度误差:常值偏置30 μg，随机偏置方差σ2=(30μg/3)2;视觉导航采样周期为Tvision=0.05 s，惯性导航采样周期为TINS=0.01 s.同时为了验证测量修正对滤波的影响，也对未采用量测修正的多速率相对导航进行仿真，仿真结果如图2～4所示.

图2 相对姿态角估计误差

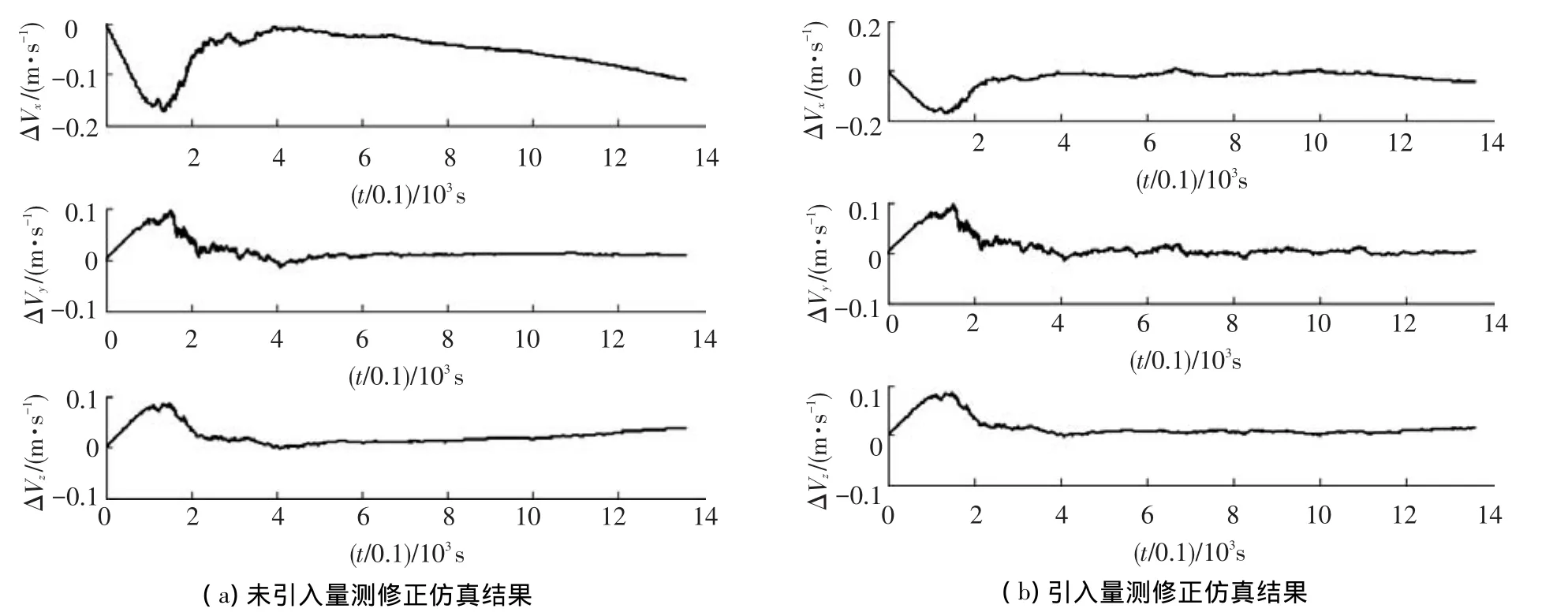
图3 相对速度估计误差

图4 相对位置估计误差

从仿真曲线可以看出两种多速率滤波方法都 能够有效处理量测信息异步的问题，在相同的仿真条件下，本文提出的算法具有更好的收敛效果.需要说明的是在无视觉辅助情况下，纯惯性组件测量时姿态趋于发散，因此不在论文中给出.

此外，对仿真结果进行了统计分析.表1比较了修正前后三轴姿态角、速度和距离误差的稳态均值.姿态角、速度和距离精度最高分别提高了0.03 °、0.02 m/s和0.3 m，表明采用量测修正的多速率组合导航滤波器具有更好的性能.因此数学仿真验证了本文提出的视觉/惯性异速卡尔曼滤波融合算法的有效性，能够完成相对导航任务需求.

表1 滤波器数据对比

5 结语

针对近距离航天器编队或在轨服务等航天任务的相对导航问题，本文采用单目视觉和惯导系统组合的相对测量方式，研究了基于测量修正的多速率卡尔曼信息融合算法.该算法既克服了惯导系统的漂移问题，又解决了视觉导航测量数据更新率低的问题.针对视觉敏感元件测量噪声不确定的缺点，提出了利用测量信息对滤波量测噪声阵和状态估计误差协方差阵进行后验修正的方法.数学仿真结果表明该方法的有效性和可行性.

［1］ WU Yunhua，CAO Xibin，XING Yanjun，et al.Relative motion coupled control for formation flying spacecraft via convex optimization［J］.Aerospace Science and Technology，2010，14:415-428.

［2］WU Yunhua，CAO Xibin，XING Yanjun，et al.Relative motion integrated coupled control for spacecraft formation via GaussPseudospectralmethod［J］.Transactions of the Japan Society for Aeronautical and Space Sciences，2009，52(177):125-134.

［3］ WU Baolin，WANG Danwei， ENG K P， et al.Nonlinearoptimization oflow-thrusttrajectory for satellite formation:Legendre Pseudospectral approach［J］.Journal of Guidance，Control，and Dynamics，2009，32(4):1371-1381.

［4］吴云华，曹喜滨，张世杰，等.编队卫星相对轨道与姿态一体化耦合控制方法研究［J］.南京航空航天大学学报，2010，42(1):13-20.

［5］李晨光，韩潮.编队飞行卫星群相对轨道测量研究［J］.北京航空航天大学学报，2005，31(6):614-617.

［6］崔小松，王惠南.基于类GPS技术的编队卫星相对参数测量研究［J］.飞行器测控学报，2012，31(3):85-89.

［7］WU Yunhua，GAO Yang，LIN Jiawei，et al.Low-cost，high-performance monocularvision system forair bearing table attitude determination［J］.Journal of Spacecraft and Rockets，2014，51(1):66-75.

［8］CRASSIDIS J L，ALONSO R，JUNKINS J L.Optimal attitude and position determination from line-of-sight measurements［J］.The Journal of the Astronautical Sciences，2000，48(2/3):891-896.

［9］CHENG Y，CRASSIDIS J L，MARKLEY F L.Attitude estimation for large field-of-view sensors［J］.Journal of the Astronautical Sciences，2006，54(3/4):433-448.

［10］YANG Y，CAO X.Design and development of the small satellite attitude control system simulator［C］//AIAA Modeling and Simulation Technologies Conference and Exhibit.Reston VA:AIAA，2006:21-24.

［11］HARALICK R M，JOO H，LEE C，et al.Pose estimation from corresponding point data［J］.IEEE Transactions on Systems，Man and Cybernetics，1989，19(6):1426-1446.

［12］曾占魁.视觉/惯性组合相对导航算法及物理仿真研究［D］.哈尔滨:哈尔滨工业大学，2007.

［13］NING X，FANG J.Autonomous celestial navigation method for LEO satellite based on unscented Kalman Filter and information fusion［J］.Aerospace Science and Technology，2007，11(2/3):222-228.

［14］GAO S，ZHONG Y，LI W.Robust adaptive filtering method for SINS/SAR integrated navigation system ［J］.Aerospace Science and Technology，2010，15(6):425-430.

［15］XING Yanjun，ZHANG Shijie，ZHANG Jinxiu，et al.Robust-extended Kalman Filterforsmallsatellite attitude estimation in the presence of measurement uncertainties and faults［J］. Proceedingsofthe Institution of Mechanical Engineers.Part G:Journal of Aerospace Engineering，2012，226(1):30-41.