基于HHT法的煤冲击破坏低频电磁信号去噪
付玉凯,杨 威,李成武
(1.天地科技股份有限公司开采设计事业部,北京100013;2.煤炭科学研究总院开采设计研究分院,北京100013;3.煤炭科学研究总院煤炭资源高效开采与洁净利用国家重点实验室,北京100013;4.中国矿业大学 (北京)资源与安全工程学院,北京100083)
随着煤矿开采深度的增加,煤矿煤岩体动力灾害日益增多,严重影响了煤矿的安全、高效生产。针对煤岩体动力灾害,预测预报是关键。目前,电磁辐射预测方法受到了国内外学者的关注[1-3]。
由于煤岩冲击破坏过程中产生的电磁信号是一种非线性、阵发性的脉冲信号,属于典型的非平稳随机信号[4],所以对其进行去噪滤波显得非常困难。因此,去噪滤波技术严重制约了电磁信号在预测预报煤岩动力灾害中的应用。目前,学者主要采用傅里叶变换 (FFT)、小波变换 (WT)等信号处理方法对电磁信号进行分析,但是这些方法只能分析信号的总体频率,不能有效分析信号的时频特性[5-6]。小波变换分析方法与其他分析方法相比,其时频分析精度依赖于小波基函数的选取,有时由于基函数选取问题,使其对信号的精细分解受到限制[7-8]。
希尔伯特黄变换 (HHT)是1998年由Huang等人[9-10]提出了一种处理非线性、非平稳信号的时频分析方法,HHT分析方法主要包括2个部分:一是多分辨经验模态分解 (EMD)和瞬时频率变换;二是对EMD分解的分量进行时频分析。HHT变换实际上是一种以傅里叶变换为基础的改进型信号处理方法,该方法在电磁信号去噪中的应用较少。
本文采用HHT时频分析方法对煤冲击破坏的低频电磁信号进行经验模式分解 (EMD),并通过对各个IMF(某一频率尺度上的模态信号)分量进行重构,最后对重构信号进行时频谱分析。
1 HHT变换原理
1.1 经验模态分解法 (EMD)原理及算法
1.1.1 EMD原理
EMD法[11]是 HHT的核心,其主要有两个作用:过滤叠加波和对称化波形。EMD可以将信号从时间尺度上进行IMF分量分解,但是需要满足下面两个条件:
(1)整个信号数据的极值点和过零点个数相差不超过1。
(2)由局部最大值所绘制的包络线和由局部最小值点所绘制的包络线的平均值为0,就是信号必须对称于时间轴。
1.1.2 EMD算法
对一个原始信号X(t),首先找出X()t上全部的最大值和最小值,然后采用插值方法对曲线进行极值拟合,从而绘制出曲线的包络线Xmax()t。同理得出包络线Xmin()t,2条包络线包含了全部信号数据。对2条包络线取其平均值得平均线m1()t,再用X()t减掉m1()t得到h1()t。如果信号不同,h1()t有可能产生一个IMF分量,也可能得到2个IMF分量。若分量不满足限定条件,此时将h1()t当做原信号,重复以上的程序,即得h11()t =h1()t -m11()t,m11()t是h1()t的2条包络线平均值;若h11()t没有变换成IMF分量,则接着计算,进行k次计算,得到第k次计算的数据h1k(t)=h1(k-1)(t)-m1k(t)。判断h1k(t)是不是可以满足IMF分量,这样就需要一个计算过程终止的法则,一般可以用2个连续结果的标准差SD作为判断依据[12-13]:

在实际运算中,可以通过对信号反复筛选来确定IMF分量,筛选结果通过SD值来确定。经验表明,当取SD=0.2~0.3时比较合适,既可确保IMF的线性和稳定性,又可使IMF具有相应的物理意义[11]。
1.2 HHT变换与时频谱
1.2.1 HHT 变换
对信号进行分解,得到IMF分量,对分量进行HHT变换,计算出其瞬时频率。对全部IMF分量进行上述变换,即HHT谱[10]。HHT变换很好地刻画了信号的局部性质,可以很好地得到信号的瞬时频率,避免了傅里叶变换中产生的不真实高低频成分,其具有直观的物理意义[10]。
1.2.2 HHT谱
HHT谱变换[14]可以把信号幅值变换为时间、频率平面上的等高线图,该变换称之为HHT时频谱。时频谱主要有3种表达形式:灰度图、等高线及三维空间图形,其表达式如下:

式中,H为信号幅值;Re为累计相加;ai()t为每一阶IMF的幅值;ωi(t)为每一阶IMF的瞬时频率。
如果对Hω,()t进行时间上积分,可以得到信号的HHT边际谱:
2 实验简介
2.1 实验系统及装置
试验系统包括两部分,即霍普金森压杆(SHPB)和电磁辐射测试系统,试验系统见图1,图2。
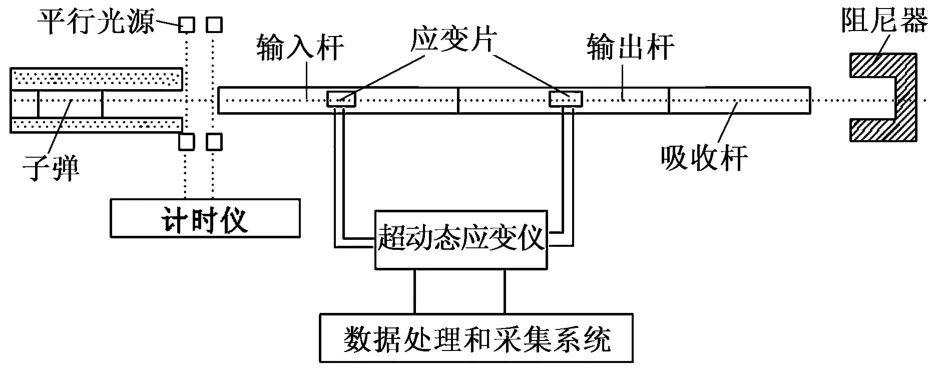
图1 实验装置

图2 实验装置实物
霍普金森压杆系统由子弹、输入杆和输出杆组成,压杆为钢质压杆,直径为50mm,子弹为φ50mm×400mm的圆柱体。被测试样夹在输入杆和输出杆之间。
选用的电磁辐射接收装置为ZDKT-1型瞬变磁振测试系统 (图2),该系统包括磁场天线、信号采集系统 (3000s-1)及计算机。实验时,天线正对煤试件,距其30~40mm。
2.2 煤样制作
煤试件来源于某矿掘进头,煤样采用圆柱体,尺寸为 φ50mm ×50mm,平行度0.02mm[15],试样两端涂抹石墨,以减少其摩擦效应[16-17]。
2.3 煤冲击破坏低频电磁信号去噪前分析
共加工12个试样,分为4组进行实验,分别记为 A1,A2,A3;B1,B2,B3;C1,C2,C3;D1,D2,D3。对每一组进行相同速率下的实验,由于煤体强度较低,经多次冲击测试发现,冲击速率大于3m/s即可破坏煤试样,且冲击速率过大会导致应力-应变曲线失真。当冲击速率在3~10m/s之间时,测试结果可靠性较高。由于子弹冲击速率是由动力系统中的高压氮气所施加的,其速率控制有一定的误差,所以冲击加载速率以平行光源测试结果为准。根据平行光源测定结果,实验的冲击速 率 分 别 为 3.287m/s,6.251m/s,6.950m/s,8.714m/s。实验结果发现,同一组实验结果的重复性较好。鉴于文章篇幅有限,以D1为典型信号进行分析,冲击速率为8.714 m/s时,最大应变率为166.35s-1,采集的低频磁场原始信号见图3。

图3 原始信号
由图3可以看出,共采集了10s的低频磁场信号,但突变的低频磁场信号介于5~7s之间,持续时间较短 (小于2s),并且信号中伴随着大量的背景噪声信号,这些噪声信号主要来自外界环境和采集系统自身[18]。存在噪声的低频电磁信号对于预测煤岩冲击破坏十分不利。为了能清楚地认识低频磁场信号的特征,需要对原始低频电磁信号进行去噪分析。为了验证HHT分析煤冲击破坏的低频磁场信号的有效性和突显信号非线性的能力,首先将原始低频磁场信号进行FFT频谱分析和Morlet时频分析[19-20]。Morlet时频分析是小波变换的一种形式,分析结果见图4和图5。
由图4和图5可以看出,信号的能量主要集中在600Hz以内,原始低频信号中存在明显的噪声成分,并且Morlet的时频分析谱的有效信号也被背景噪声信号掩盖,从上面2个图很难清楚认识有效信号随时域和频域的动态变化特征,这就需要进一步采用HHT法对信号进行去噪分析。
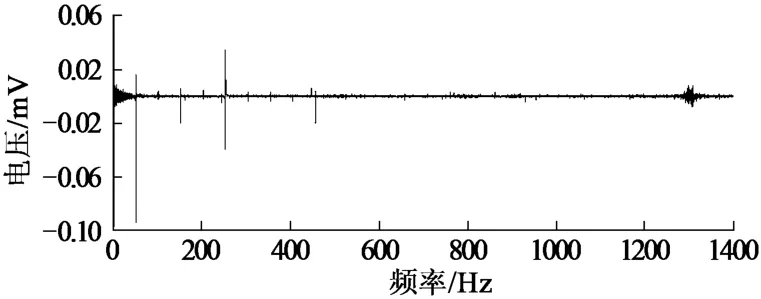
图4 原始信号的FFT谱

图5 原始信号的Morlet时频谱
3 低频磁场信号的HHT分析
3.1 磁场信号的EMD分解及重构
低频电磁信号属于非平稳脉冲信号,在煤岩冲击破坏过程中有时某一时间段的信号强度大,那么信噪比就较高;而另一时间段信号强度较弱,这时信噪比就很低。如果采集到的信号强度一直较低,那么会严重影响信号的采集质量[21]。如果在信号分析时,我们能选择能量强的信号进行分析,而舍弃那些能量弱的信号 (信号强弱跟煤岩体破裂程度相关),这样才能得到原始信号中的有效信号。其他信号处理方法难以完成上述问题,这也是HHT方法能完成这一问题的关键。
首先运用HHT中的经验模态分解方法,即EMD分解,可以得到原始低频磁场信号的有限数目的IMF分量。由于信号的特征尺度参数都是基于所采集信号,所以,EMD所筛分出来的IMF分量都具有实际物理意义,每个IMF分量代表了某一频率尺度上的模态。图6是低频电磁信号的EMD分解图,该信号共分为11阶IMF分量,在时间域上表示从小尺度到大尺度的层层筛选滤波。
从图6可以看出,IMF_h1~IMF_h5分量包含大量的噪声信号 (外界环境噪声和采集系统噪声);IMF_h6~IMF_h10分量噪声信号较低,其属于低频磁场信号的优势分量,为信号优势频率分量;IMF_residual分量表示磁场信号的变化趋势,通常称之为残余分量。
将IMF_h6~IMF_h10分量进行重构,重构信号见图7所示。由图7可以看出,重构的信号能很清晰地刻画出低频磁场信号的非线性、非平稳性,很好地表示出了信号的时频特征——磁场信号初期线性上升,然后指数衰减,最后尾部小幅震荡[22-23]。

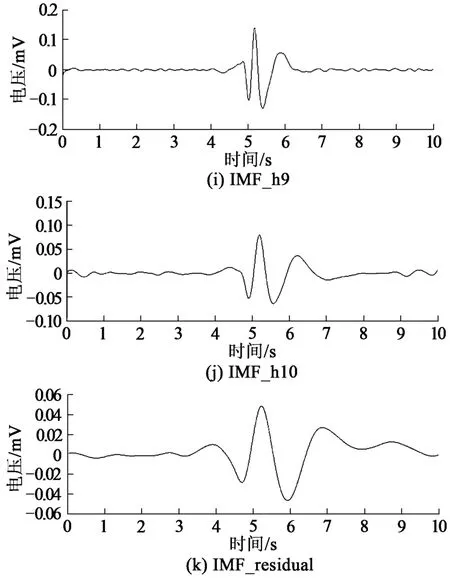
图6 原始信号EMD分解

图7 去噪重构信号
将重构的信号进行FFT变换,得到信号的幅值-频率图 (图8)。由图8可以看出,煤冲击破坏产生的低频磁场信号的优势频率较低,范围在0~40Hz之间,对另外几组煤样进行实验。采用上述分析方法后,分析结果基本相同。
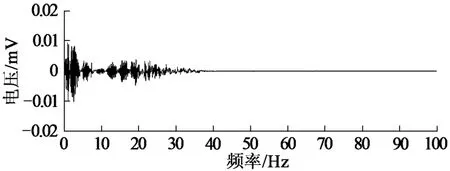
图8 重构信号的频域
3.2 重构信号的时频谱分析
图9 (a)是对重构信号进行的HHT时频谱,从图中可以看出,颜色越亮表示其能量越高,反之越低;HHT时频谱直观地表现出了信号的聚集性,与原始信号的时频谱 (图5)相比,可以很清晰地看出能量随时间和频率的变化。显然,在0~100Hz频段内,整个时域上的能量都较强;在时间域上,第5s至第6s时间域上的能量较强,该时间域对应于煤的冲击破坏时间。
图9(b)表示重构信号的边际时间,表示每个时间在全局上的幅度之和,是表示时间点上信号能量强弱的一个指标,从该图中也可以看出,第5s至第6s时间域上的能量较强,很好地验证了HHT时频谱分析的正确性。
图9(c)表示重构信号的边际谱,表示在每个频域上全部幅值的总和,由图可以看出,0~40Hz范围的边际谱比较大,这也说明了信号能量的主要频域集中在0~40Hz,分析结果与图8相吻合。

图9 重构信号的HHT时频谱、边际时间和边际谱
总之,HHT方法可以有效地对煤冲击破坏的低频磁场信号进行滤波去噪,可以很好地表示磁场信号的时频动态非线性、非平稳性及脉冲特性,可以表现出信号时域上的频率和能量差异,与其他信号处理方法相比,有其独特的优势。由上述分析可以看出,HHT时频分析方法为煤岩体冲击破坏磁场信号的滤波处理提供了一种新的方法。
4 结论
(1)采集到的煤冲击破坏低频电磁信号持续时间较短 (1~2s),并且信号中存在大量的背景噪声。通过对原始信号进行FFT频谱分析和Morlet时频分析,得出原始信号的能量主要集中在600Hz以内;并且Morlet时频分析谱的有效信号被背景噪声信号完全掩盖。
(2)HHT法中的EMD可以很好地分解原始磁场信号,然后得出其IMF分量,每个IMF分量都有其特定的物理意义,通过对有效IMF分量进行重构,重构信号能很好地刻画出低频电磁信号的非线性、非平稳性及脉冲特性。
(3)通过对重构信号进行时频谱分析,可以很清晰地看出能量随时间和频率的变化,并且得出低频磁场信号的优势频率在0~40Hz之间,能量最强点位于信号的第5~6s之间。
(4)与其他分析方法相比,HHT分析方法具有完全的局部时频特征,可以准确地刻画低频磁场信号的动态变化特征,且可以很好地刻画信号的突变点信息,这为低频电磁信号的检测、信号滤波、数据筛选等提供了有利条件。
[1]何学秋,刘明举.含瓦斯煤岩破坏电磁动力学[M].徐州:中国矿业大学出版社,1995.
[2]王恩元,何学秋.煤岩变形破裂电磁辐射的实验研究 [J].地球物理学报,2000,43(1):131-137.
[3]聂百胜,何学秋,王恩元,等.煤体剪切破坏过程电磁辐射与声发射研究 [J].中国矿业大学学报,2002,31(2):609-611.
[4]朱郴韦.煤体破裂电磁辐射信号波形特征及降噪方法研究[D].北京:中国矿业大学 (北京),2009.
[5]Cohen L.Time-frequency analysis[M].New Jersey:Prentice Hall,1995.
[6]谢 中,程迎军,徐清燕.电解气泡析出时电位波动的频谱分析[J].中国有色金属学报,2003,13(4):1011-1016.
[7]刘希灵,李夕兵,洪 亮,等.基于离散小波变换的岩石SHPB测试信号去噪[J].爆炸与冲击,2009,29(1):67-72.
[8]周子龙,李夕兵,龙八军.岩石SHPB试验信号的小波包去噪[J].岩石力学与工程学报,2005,24(S1):4780-4783.
[9]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-station time series analysis[C].Proceeding of the Royal Society of London,1998.
[10]Yue H Y,Guo H D.A SAR.Interferogram filter based on the empirical mode decomposition method[C].Proceedings of Geosoience and Remote Sensing Symposium.IGARSS O1,2001.
[11]Semion Kizhner,Thomas P Flatley,et al.On the Hilbert- Huang transform data processing system development[A].2004 IEEE Aero pace Conference Procedings[C].2004:1961-1979.
[12]李夕兵,凌同华,张义平.爆破震动信号分析理论与技术[M].北京:科学出版社,2009.
[13]Norden E Huang,Zheng Shen,Steven R Long,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].The Royal Society,1998,454:903-995.
[14]武安绪,吴培稚,兰从欣,等.Hilbert-Huang变换与地震信号的时频分析[J].中国地震,2005,21(2):207-216.
[15]李胜林,刘殿书,李祥龙,等.75mm分离式霍普金森压杆试件长度效应的实验研究[J].中国矿业大学学报,2010,39(1):93-97.
[16]ZENCKER U,CLOS R.Limiting conditions for compression testing of flat specimens in the Hopkinson pressure bar[J].Experimental Mechaincs,1998,39(4):343-348.
[17]WEINONG W,CHEN B S.Split Hopkinson(Kolsky)bar design,testing and applications[M].Springer New York Dordrecht Heidelberg London,2011:7-17.
[18]李成武,解北京,杨 威.基于HHT法的煤冲击破坏SHPB测试信号去噪 [J].煤炭学报,2012,37(11):1796-1801.
[19]Daubechies I.小波十讲[M].李建平,杨万年,译.北京:国防工业出版社,2004:38-40.
[20]付玉凯,李成武,段昌瑞,等.煤体失稳破坏过程中的低频磁场变化特征研究 [J].煤矿开采,2014,19(4):13-17,76.
[21]林 君,项葵葵,朱宝龙,等.MT信号现场处理的实现技术研究[J].数据采集与处理,1997,12(1):52-55.
[22]李成武,解北京,杨 威.煤冲击破坏过程中的近距离瞬变磁场变化特征研究 [J].岩石力学与工程学报,2012,31(5):973-981.
[23]程 磊,瞿伟廉.基于Hilbert-Huang变换理论的非平稳数据处理[J].建筑科学与工程学报,2007,24(1):26-30.

