基于显式有限体积法的一维河网模型

向小华,吴晓玲,牛 帅,杜世鹏

(1.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2. 河海大学水文水资源学院,江苏 南京 210098; 3. 南京水利科学研究院水文水资源研究所,江苏 南京 210029; 4. 浙江省水利水电勘测设计院,浙江 杭州 310002)

基于显式有限体积法的一维河网模型

向小华1,2,吴晓玲2,牛 帅3,杜世鹏4

(1.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2. 河海大学水文水资源学院,江苏 南京 210098; 3. 南京水利科学研究院水文水资源研究所,江苏 南京 210029; 4. 浙江省水利水电勘测设计院,浙江 杭州 310002)

采用显式通量差分裂格式离散圣维南方程组,通过特征线方式处理边界;在局部离散中引入跨临界流熵修正和TVD限制器,以提高模型精度并保证模拟稳定性,最终构建了基于显式有限体积法的一维河网水流模型。经典算例验证表明,所建立的模型能够处理具有激波的跨临界等复杂流态;模型应用于长江南京八卦洲河段,水位和流量的验证表明该模型能够应用于实际的河网,并具有较高的精度,为显式离散方法应用于河网模型提供了一种思路。

一维河网模型;有限体积法;显式离散;通量差分裂;圣维南方程组

以Preissmann离散格式为基础的数值方法以及分级求解技术在大范围的河网模型中已经成为最常用的手段[1-2],其优势是模型可以采用较大的时间步长,且通过分级技术将大范围河网的整体求解问题划分为河道以及河网节点分步骤求解问题,在效率和计算硬件需求上都有较大优势[3-4]。但Preissmann格式在没有经过特殊处理时难以适应跨临界流等特殊流态[5-6];且该格式在实际应用中只具有一阶精度,在河网应用中存在误差累积[7];另外,线性化的圣维南方程组需要迭代求解,当迭代不收敛时将不仅耗费工作量且得不到满意的结果。

流体力学的另一分支——计算气动力学在数值精度以及稳定性方面都取得了重要进展,总变差衰减(total variation diminishing,TVD)类方法是其中重要的理论成果[8]。由于水和气的相似性,气动力学方法被广泛地移植到水流计算中[9-11],结果显示新方法精度较传统水力学方法有明显提升,表明方法移用在理论上是可行的。但气动力学方法的理论和实际应用多是基于显式离散方法,而目前的河网模型则几乎都基于隐式离散方法,如何将气动力学的成果应用于河网模型就需要解决显式方法的适用性问题。本文以显式的通量差分裂格式为例,以河网三级解法为基础构建显式河网模型,为显式格式的应用提供一种思路,方程的详细离散过程已经在文献[12]中加以描述,本文不再赘述,本文的重点在边界条件处理以及显式河网模型构建,并将所构建的河网模型应用于一个经典算例和长江南京八卦洲河段的水流模拟,分别用于验证模型处理跨临界流以及捕捉受潮汐影响河段的潮位和流量过程的能力。

1 控制方程

一维非守恒型圣维南方程组的矩阵形式为

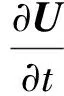
(1)

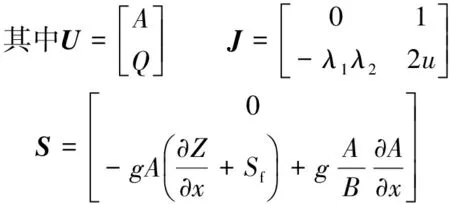
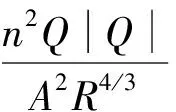
式中:U为待求向量;J为方程组特征矩阵,其两特征值分别为λ1=u-c、λ2=u+c,c为重力波速,u为断面平均流速;S为源项;A为过水断面面积;Q为过水断面流量;g为重力加速度;B为水面宽度;Z为断面水位;Sf为摩阻比降;R为水力半径;n为曼宁糙率。

2 数值方法

2.1 数值离散

TVD类方法中的通量差分裂格式物理意义为:控制体内物理量的变化是由进入控制体的净通量差引起的,其含义见图1。针对控制体i,式(1)可以离散成如下形式[12]

(2)

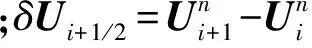
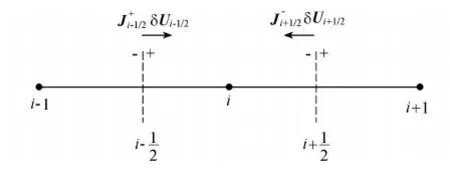
图1 控制体示意图

为了保证格式的和谐性[12],将式(2)中的Si也采用分裂离散,整理后得

(3)

2.2 边界条件处理

采用特征线方法,在河道首断面1得到的离散方程[12]为

(4)

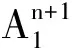
(5)

断面1上还需要给定一个边界条件才能形成闭合方程组。同样的方法,在河道的末断面N的有效方程的概化形式为

(6)

需要另外补充边界条件才能封闭。

2.3 河网模型构建

河网模型三级解法的步骤分3步:①将单河道内部的状态采用河道首末断面的水位线性表达;②在节点处根据能量和水量平衡建立节点水位方程,进而建立流域节点水位方程组,求解得节点水位;③将节点水位回代到各河道中完成一次求解。而在显式方法中,单河道内部的状态已经与边界条件解耦,无须内部线性表达和回代过程,即省去了第①③步,在第②步中也只针对节点单独建模求解,各节点之间也没有直接关联,无须求解节点水位方程组。

以图2所示的一个河网节点i为例,说明节点的水位方程构建。图2中两条河流入节点,节点处的断面编号分别为N1和N2,流出节点的河道首断面编号为1。在节点处满足的相容条件为断面N1、N2以及1水位相等;断面1流量为断面N1、N2流量之和,即

(7)

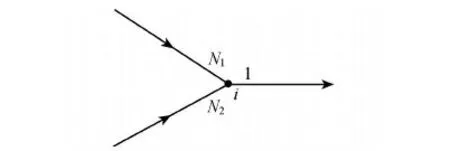
图2 河网节点示意图

将式(5)和式(6)分别代入式(7),最终将求得节点处各河道的水位和流量,完成河网的一次求解。本文所采用的方法虽然采用了非守恒型方程(1),但只要按照文献[9]中的方式计算矩阵J,则仍能保证物理量的守恒性,即式(1)和守恒型圣维南方程组等价。由于采用的是显式计算方法,计算过程无须迭代求解,节省了工作量,避免了隐式线性化不收敛的问题。整个河网模型均是简单的数值计算,无须隐式方法中的矩阵求解过程,便于方法的理解和实现。

3 算例分析

3.1 跨临界流算例

本算例是一个经典的算例,用来测试数值算法处理激波及跨临界流的能力[13]。算例采用矩形断面河道,河道长25 m、宽1 m,河底地形有一弧形凸起,定义为

(8)

通过设定恒定的边界条件,最终将得到恒定流状态,所设置的条件为

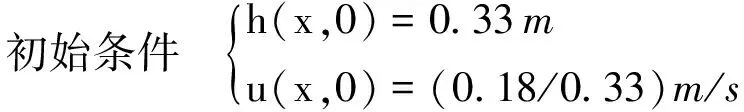
(9)

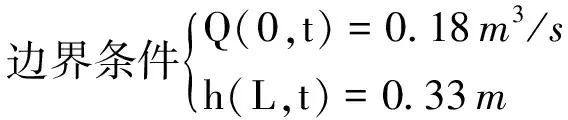
(10)

式中:h为断面水深;u为断面流速;Q为断面流量。

在以上条件下会形成具有激波的跨临界流,这对于数值方法具有一定的挑战,未经特殊处理的Preissmann离散方法无法模拟该算例,采用本文所建立的模型,均匀划分200个断面,断面间距0.125 m,显式计算的时间步长受CFL条件限制,其中CFL数取0.9。模拟结果如图3所示,数值解与精确解完全吻合,最大误差不超过5 mm,表明本文所述的方法具有处理复杂的临界流态的能力。

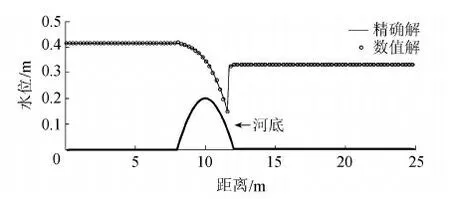
图3 激波跨临界流数值解与精确解对比

3.2 实际河网算例

八卦洲位于长江下游的南京市,将长江分割为南部的主流和北部的支流,形成环状河网。此河段受长江口潮汐影响明显,潮位呈现出规律的每天两高两低潮特征,本次模型建模范围上游从南京潮位站开始,下游至西坝潮位站,区间干流长度约20 km,八卦洲支流长度约21 km。河段内有上元门、燕子矶、工程段、扬吧以及通江集等潮位站。为了建设港口等工程,水文部门在2006年4月8—10日以及2007年4月8—10日对河段内的潮位过程进行了测量,并在第二时间段扬吧站所在断面进行了半潮流量测量。全河网共划分176个计算断面,平均断面间距180 m。以南京站作为上边界,西坝站作为下边界,内部潮位站点实测潮位过程和扬吧实测流量过程用来验证方法的精度。在计算过程中,首先以上边界的初始水位作为全河道水位,然后以上、下边界实测初始值作为边界计算恒定流,恒定后的水位作为正式计算时的初始水位;经过前期资料率定,该河段的河道糙率取为0.020。与上述地理描述对应的模型断面分布、河网节点布置、水位站点位置等见图4。

图4 八卦洲河网形态

水位、流量实测与模拟对比过程见图5,两者比较吻合,精度分析见表2。水位与流量的实测值与模拟值的相关系数在0.991～0.999之间,确定性系数在0.955～0.995之间,最大水位均方根误差不超过0.04 m;扬吧断面的流量均方根误差为126.75 m3/s,相对误差为4.6%,模型很好地捕捉到了完整涨落潮过程和潮位波动的流量过程,具有较高的精度。

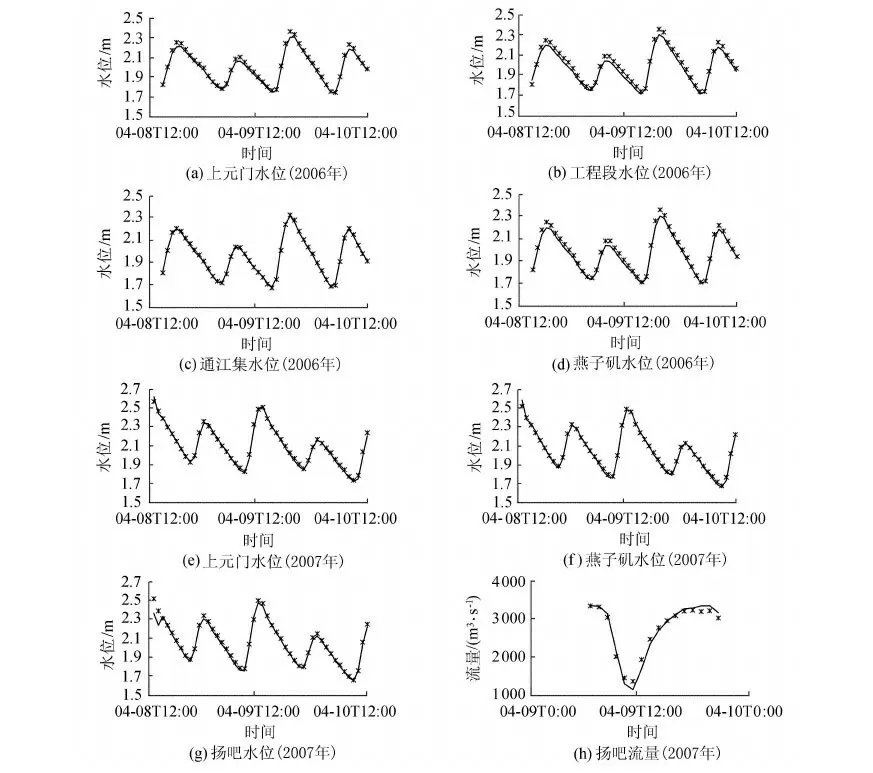
图5 长江南京八卦洲河段水位与流量对比

表2 各测站模拟精度分析

4 结 论

本文基于显式通量差分裂格式离散圣维南方程组,建立了河道一维显式水动力模型。依据河网三级解法的思路,建立节点处的相容方程,回避了隐式河网模型中所需的递推和回代过程,建立了显式格式下的河网模型,提供了一种将显式TVD格式应用于河网模型的方法。理想模型的结果显示本文模型能够处理具有激波的跨临界流流态;长江南京八卦洲河段的实例验证表明模型能够有效地模拟涨落潮水位以及潮流流量。

[1] 张二骏,张东生,李挺.河网非恒定流三级联合算法[J].华东水利学院学报,1982(1): 1-13.(ZHANG Erjun,ZHANG Dongsheng,LI Ting.Three steps method to compute unsteady flow for river networks[J].Journal of East China Institute of Water Resource,1982(1): 1-13.(in Chinese))

[2] 侯玉,卓建民,郑国权.河网非恒定流节点分组解法[J].水科学进展,1999,10(1): 48-52.(HOU Yu,ZHUO Jianmin,ZHENG Guoquan.Unsteady flow computation using junctions group method in river network[J].Advances in Water Science,1999,10(1): 48-52.(in Chinese))

[3] 朱德军,陈永灿,王智勇,等.复杂河网水动力数值模型[J].水科学进展,2011,22(2): 203-207.(ZHU Dejun,CHEN Yongcan,WANG Zhiyong,et al.Hydrodynamic model for complex flow in open-channel networks[J].Advances in Water Science,2011,22(2): 203-207.(in Chinese))[4] XIE Zuotao,YANG Fangli,FU Xiaoli.Mathematical model for flood routing in Jingjiang River and Dongting Lake network[J].Water Science and Engineering,2012,5 (3): 259-268.

[5] 茅泽育,相鹏,黄江川,等.Preissmann四点隐格式对计算混合流动的适定性分析[J].科学技术与工程,2007,7(3):343-347.(MAO Zeyu,XIANG Peng,HUANG Jiangchuan,et al.Study on the invalidity of preissmann scheme for transcritical flow[J].Science Technology and Engineering,2007,7(3):343-347.(in Chinese))

[6] DJORDJEVIC S,PRODANOVIC D,WALTERS G A.Simulation of transcritical flow in pipe/channel networks[J].Journal of Hydraulic Engineering,2004,130(12): 1167-1178.

[7] 杨开林,白正裕.调水渠网非恒定流的线性变换求解方法[J].水利学报,2004,35(3): 35-41.(YANG Kailin,BAI Zhengyu.Linear transformation method for calculation of unsteady flow in water diversion networks[J].Journal of Hydraulic Engineering,2004,35(3): 35-41.(in Chinese))

[8] ETORO E F.Riemann solvers and numerical methods for fluid dynamics: a practical introduction[M].3rd ed.Berlin:Springer-Verlag,2009.

[9] 谭维炎.计算浅水动力学:有限体积法的应用[M].北京: 清华大学出版社,1998: 153-172.

[10] 向小华,吴晓玲,王春艳,等.基于通量差分裂的圣维南方程组离散方法[J].河海大学学报:自然科学版,2012,40(1): 59-62.(XIANG Xiaohua,WU Xiaoling,WANG Chunyan,et al.Discrete for Saint-Venant equations based on flux difference splitting scheme[J].Journal of Hohai University: Natural Sciences,2012,40 (1):59-62.(in Chinese))

[11] 向小华, 吴晓玲, 王船海. 通量与源项和谐的一维浅水方程离散方法[J].河海大学学报：自然科学版, 2009, 37(6): 721-726. (XIANG Xiaohua,WU Xiaoling,WANG Chuanhai. Well-balanced discrete method for determining flux and source terms in 1-D shallow water equations[J]. Journal of Hohai University：Natural Sciences, 2009, 37(6): 721-726. (in Chinese))

[12] 向小华,吴晓玲,牛帅,等.通量差分裂方法在一维河网模型中的应用[J].水科学进展,2013,24(6):894-900.(XIANG Xiaohua,WU Xiaoling,NIU Shuai,et al.An application of flux difference splitting scheme in river-network model[J].Advances in Water Science,2013,24(6): 894-900.(in Chinese))

[13] VAZQUEZ-CENDON M E.Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry[J].Journal of Computational Physics,1999,148(2):497-526.

Construction of one-dimensional river network model based on explicit finite volume method//

XIANG Xiaohua1, 2, WU Xiaoling2, NIU Shuai3, DU Shipeng4
(1.StateKeyLaboratoryofWaterResourcesandHydropowerEngineeringScience,WuhanUniversity,Wuhan430072,China; 2.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China; 3.HydrologyandWaterResourcesDepartmentofNanjingHydraulicResearchInstitute,Nanjing210029,China; 4.ZhejiangDesignInstituteofWaterConservancyandHydro-ElectricPower,Hangzhou310002,China)

A one-dimensional river network model was constructed by discretization of Saint-Venant equations with explicit flux-difference splitting scheme and dealing border with characteristic line method. Meanwhile, the modeling accuracy and stability are enhanced with the application of entropy correction and total variation diminishing(TVD) limiter to local discretion. In a classical numerical example, the model shows its ability in capturing complex flow conditions like trans-critical flow with shock waves. Being applied in the Baguazhou section of the Yangtze River, the model shows its performance in terms of water level and flux with higher accuracy, which is suitable for the real river network. To sum up, the model discretion introduces a new idea about explicit discretion into river network model.

one-dimensional river network model; finite volume method; explicit discretion; flux difference split; Saint-Venant equations

武汉大学水资源与水电工程科学国家重点实验室开放基金(2013B105);国家自然科学基金(41201030)

向小华(1981—),男,湖北松滋人,讲师,博士,主要从事水文模型研究。E-mail:xxh_xiang@sina.com

10.3880/j.issn.1006-7647.2015.04.002

TV133

A

1006-7647(2015)04-0006-04

2015-01-04 编辑：熊水斌)