简单记忆混沌系统同步控制的研究

陆安山

（钦州学院物理与电子工程学院，广西 钦州535000）

混沌是一种具有初值敏感性、遍历性等极端复杂动力学行为的确定性系统，因在生物学、医学、电子信息等方面有巨大的应用价值和潜力，吸引了各领域科学工作者广泛研究混沌的建构、非线性电路实现、保密通信、控制同步[1-3]等，并取得了丰硕的成果。混沌的同步自1990年Ott、Grobogi和Yorker提出OGY方法[4]，成功控制混沌稳定在周期轨道后，Pecora和Corroll首次提出混沌同步[5]的概念，并在实验室用电路实现这一同步控制思想，引起人们的广泛关注，迅速成为人们研究的热点之一。研究者按照混沌不同的同步形式如延迟同步、完全同步、广义同步、投影同步等，提出了如非线性控制、滑模控制、自适应控制等多种混沌同步方法[6-8]，混沌现象也开始从负面的作用走上正面利用的道路。文献[9]提出一个包含H部件[10]、仅含一个非线性项的新三维非线性系统（Wu系统），并研究其记忆效应和混沌特性。通过数值分析和设计电路实现，验证该系统是一个含广义记忆元件、单涡卷吸引子，存在分岔、混沌和阵发混沌等复杂动力学行为的混沌系统。该文主要研究在非线性耦合函数作用下，该系统（Wu系统）的同步以及同步控制器的寻获问题。

1 简单忆阻混沌系统

武花干等人在文献[9]提出一个含有H部件、仅含一个非线性项的新三维非线性动力学系统，其模型如下。

理论分析了该系统的广义记忆元件特性、混沌动力学行为，并用数值模拟和电路设计手段，相互验证了该系统是一个含有H部件的简单记忆混沌系统。对不同μ的参数值有不同的动力学行为，当μ≥0.831时系统完全进入混沌状态。系统（1）式状态变量x随参数μ变化的分岔图如图1所示。当μ=0.95时，式（1）的部件H的广义记忆元件的z（t）h（t）曲线如图2所示，吸引子yz相图如图3所示，时域波形图如4所示。

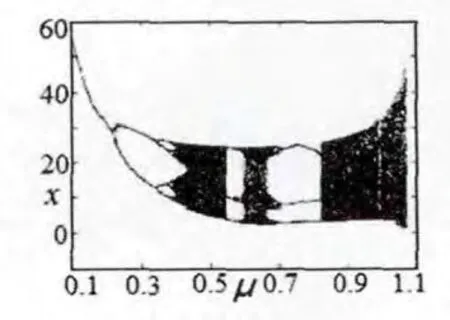
图1 μ-x分岔图

图2 z（t）-h（t）曲线

图3 y-z曲线

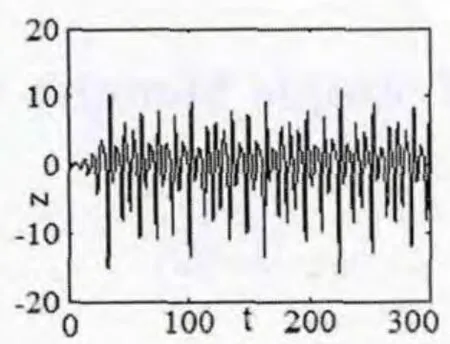
图4 t-z曲线

研究还表明该简单忆阻混沌系统仅存在一个确定的平衡点，其动力学行为依赖于可调参数μ。μ取不同值时，系统的行为可由倍周期分岔通向混沌道路，在μ=0.476、0.6、0.856、0.898处，存在阵发混沌现象。该简单忆阻混沌系统（1）存在复杂的动力学行为。

2 简单忆阻混沌系统的同步

2.1 理论分析

该文用非线性函数耦合同步法[11-12]进行控制同步。设给定连续混沌系统为X˙（t）=F（X（t），t），适当分离为：

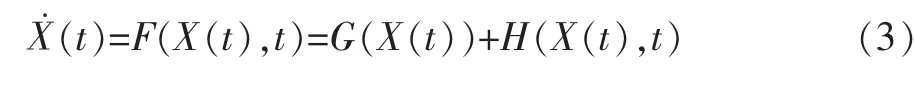
其中X（t）∈Rn是系统的n维状态矢量，G（X（t））为X˙（t）的线性部分，且有G（X（t））=AX（t），A为满秩的常数矩阵，其特征值的实部全部为负。是的非线性部分。同理，可构造一个新的连续混沌响应系统：

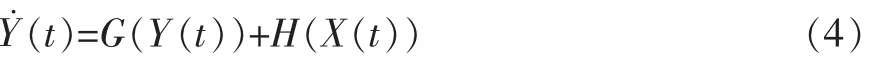
Y（t）∈Rn是系统的n维状态矢量，则系统（3）和（4）的同步误差定义为e（t）=Y（t）-X（t），可得=G（Y（t））-G（X（t））。

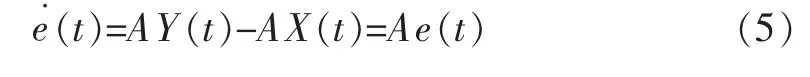
对于简单忆阻混沌系统（1），驱动系统为：

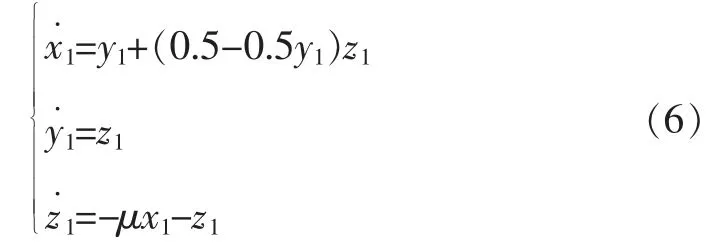
响应系统为：

设

可得驱动与响应系统的误差函数为

当取非线性控制器为

则

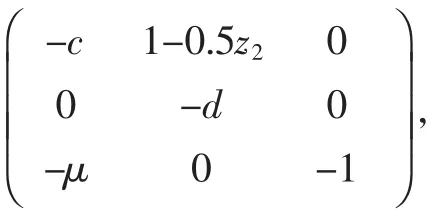
其中满秩的常数矩阵为A=则其三个特征根分别为λ1=-c、λ2=-d、λ3=-1。当c＞0、d＞0时，满秩矩阵A的三个特征根均小于零，根据Routh-Hurwitz判据知，误差系统（9）渐近稳定，则驱动系统（6）和响应系统（7）达到同步。

2.2 数值仿真

该文用matlab数学软件对简单忆阻混沌系统（1）的误差系统进行数值仿真研究。取驱动系统、响应系统为和误 差 系 统 初 值 分 别 为：x1（0）、y1（0）、z1（0）=-10，x2（0）、y2（0）、z2（0）=10，e1（0）、e2（0）、e3（0）=20，μ=0.95，c=2.5，d=2，则时间t与驱动和响应系统对应变量的变化图如图5所示，同步误差效果如图6所示。可见te1=3.426s、te2=2.815s和te3=3.836s时，误差e1（t）、e2（t）和e3（t）已稳定到零点，驱动和响应系统达到同步。

3 结语

该文利用非线性函数耦合混沌同步法，研究简单记忆混沌系统的同步问题。通过误差系统构建特征值实部皆为负值的常满秩矩阵，从而求解同步控制器，实现简单记忆混沌系统的驱动与响应系统达到同步目标。该方法使得同步控制器更易于寻获，理论和数值分析都验证了该同步方法的正确性，为同步控制器易寻获性提供了有益的思路。

图5 时间与驱动、响应系统对应变量的变化图

图6 误差系统同步响应曲线

［1］Lorenz EN.Deterministic Nonperiodic Flow［J］.Journalof the Atmospheric Sciences，1963：20（2）:130–141.

［2］Buscarino，Arturo，Famoso et al..，Luigi.Chua's Circuit Dynamics Controlled by Using aWater Electrolytic Cell Component［J］.INTERNATIONAL JOURNAL OF BIFURCATION AND CHAOS，2014，24（9）:1910-1914.

［3］陆安山，陆益民.一种变形Liu混沌系统的分析及电路实现［J］.江西师范大学学报：自然科学版，2014，38（5）:32-35.

［4］Ott E，GrebogiC，Yorke JControlling chaos［J］.Physical Review Letters，1990，64（11）:1196-1199.

［5］Pecora L M，Carroll T L.synchronization in chaotic systems［J］.PhysicalReview Letters，1990，64（8）:821-824.

［6］Moreno A，Osorio M.Lyapunov approach to second-order sliding mode controllers and observers.In:Proceedings of the IEEE Conference on Dicision and Control.Cancun，Mexico:2008，2856-2861.

［7］Li Dekui，Lian Yuping.Hybrid function projective synchr onization and parameters identification of different dimension chaotica system［J］.Journal of Qingdao Technological University，2013，34（3）:95-101.

［8］Wang Jiankui，Chen Xiangqing，Fu Jiankuan.Adaptive fi nite-time control of chaos in permanentmagnet synchronousmotor with uncertain parameters［J］.NONLINEAR DYNAMICS，2014，78（2）:1321-1328.

［9］武花干，包伯成，冯霏.简单记忆混沌系统的动力学分析与电路实现［J］.四川大学学报：工程科学版，2014（1）:134-139.

［10］Di Ventra M，Pershin Y V，Chua L O.Circuit elements with memory:Memristors，memcapacitors，and meminductors［J］.Proceedingsof the IEEE，2009，97（10）:1717-1724．

［11］张旭东，俞建宁，郭兰平，等.一个新混沌系统的非线性耦合同步的研究［J］.云南民族大学学报：自然科学版，2011（02）:149-151，156.

［12］NIEWen Jie，LANYue Heng，LIYong，etal..Generating large steady-state optomechanical entanglement by the action of Casimir force［J］.Science China（Physics，Mechanics&Astronomy），2014，12:2276-2284.

［13］LiXiaojuan，Xu Zhenyuan，Xie Qingchun，etal..Generali zed synchronization of two different unidirection coupled Lorenz systems［J］.Actaphysica sinica，2010，59（3）:1532-1539.