RC 桥式正弦振荡电路输出信号幅值特性研究

王 俭，潘欣裕，毕自强

（苏州科技大学 电子与信息工程学院，江苏 苏州215009）

正弦波振荡器在电子系统中有非常广泛的应用，不同的应用场合对振荡器两个性能指标(幅值和频率)的要求不尽相同。 有的对频率性能要求较高，有的对幅值性能要求较高，有的则对两者均有较高要求。 因此，正弦振荡信号的幅值与电路结构、元件特性及参数的确定关系是值得研究的问题。 虽然高燕梅等[1]对LC 振荡电路的起振特性做了分析研究、陈大钦[2]和Gonzalez[3]对个别结构的RC 桥式正弦波振荡电路给出了稳态正弦电压幅值的近似计算公式，任骏原[4]通过虚拟实验证实稳态正弦电压幅值与起振时电压放大倍数有关，但，对一般的RC 桥式正弦波振荡电路， 尚未见稳态正弦电压幅值定量计算方法及公式的报道。 本文首先从RC 桥式 （Wienbridge）振荡电路正负两个反馈平衡的角度出发，找出正弦振荡电压幅值的决定机制， 再针对不同实现方式的RC 桥式振荡电路推导出正弦电压幅值表达式，最后通过虚拟实验予以验证。

1 决定输出电压幅值的机制

对RC 桥式振荡电路（图1a）工作过程的普遍描述[5－6]是基于闭环概念的：当放大环节传递函数Av=1+R2/R1和反馈环节传递函数乘积的绝对值。

如果将注意力从RC 桥式振荡电路的整个闭环结构缩小到其中的反馈电路， 一个是反馈系数恒定的正反馈电路——选频电路， 另一个是反馈系数从小到大变化的负反馈电路——时变/非线性电阻分压电路，则不难发现：振荡电路从起振到稳定的全过程， 事实上正是这两个反馈从正强负弱到正负相等的过程。 因此，决定稳态正弦电压幅值的关键因素，必须从两个反馈的平衡条件予以导出。

记选频电路的正反馈常系数为Fv+，记时变电阻分压电路的负反馈变系数为Fv－(t)（图1(b)）。 在起振时和建立振荡过程中，由于Fv－(t)＜Fv+，有

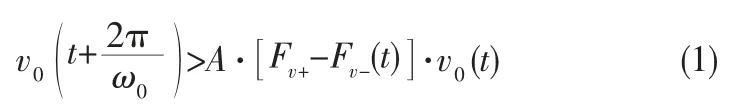
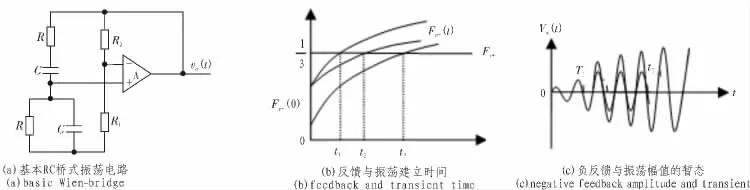
图1 RC 桥式振荡电路中反馈与振荡幅值的关系Fig. 1 The relation between feedback and amplitude of sinusoidal in Wien-bridge

随着负反馈电路中时变/非线性元件的作用下Fv-(t) 逐渐增大，直至时，，就是等幅振荡过程。显然，振荡建立过程所需的时间和稳态正弦波幅值均与Fv-(0)和Fv-(·)有关（参见图1(c)）。

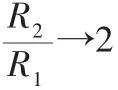
Fv-→Fv+，即，亦即。 假设R1是时变/非线性电阻，对RC 桥式振荡电路而言，无论其电阻分压负反馈回路的具体构成是怎样的， 其稳态输出电压幅值Vom都由决定。设函数R1(·)的反函数存在且记为，

则稳态正弦波幅值

式（2）就是适用与RC 桥式振荡电路输出正弦电压幅值的一般计算公式。

2 电压幅值的计算和分析

典型的RC 桥式振荡电路的负反馈回路有场效应管漏源电阻式、二极管稳幅式、热敏电阻式，本节根据上节得出的影响输出电压稳态幅值的因素及公式（2）依次进行计算，得到各自的输出电压稳态幅值表达式。

2.1 场效应管漏源电阻式

场效应管漏源电阻式振荡电路如图2 所示。

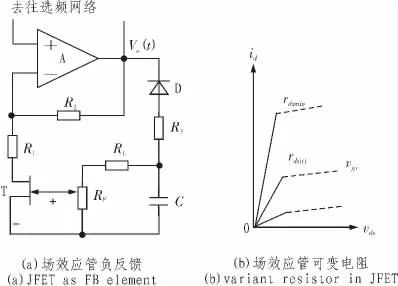
图2 场效应管漏源电阻式振荡电路Fig. 2 Oscillator with d-s resistor of JFET

设图2(a)电路处于起振过程中，其输出电压vo(t)=vom(t)sin(ωt+φ)，半波整流滤波[6]后的得场效应管的栅源电压vgs(t)≈。 随着vom(t)的逐步增大，由下式隐含的场效应管可变电阻区的漏源电阻也逐步增大。

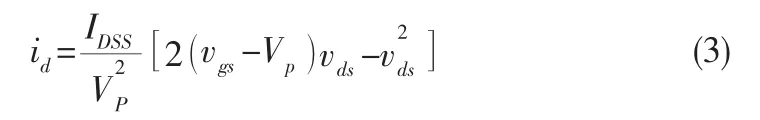
当vgs(t)和vds(t)逐渐稳定为直流电压VGS和VDS时，vom(t)也逐渐趋于Vom，合理令VDS＜＜1，可得达到最大值的漏源电阻，至此，根据式（2）可得输出电压稳定幅值为

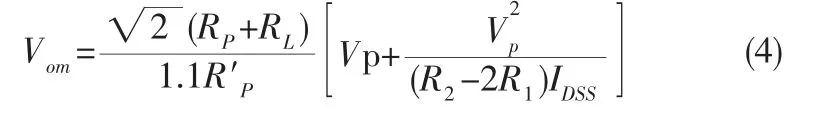
采用场效应管构成时变电阻的优点是一旦振荡电路达到稳定， 则场效应管电阻的阻值不再改变， 相应的负反馈系数Fv-也不再改变。

2.2 热敏电阻式

设图1a 中R1是正温度系数热敏电阻，其温度特性为

其稳态时的阻值R1Ts和温度Ts满足R1Ts=R10eB(T-T0)。 忽略在热平衡状态下电能转换热能的时间，可得。 结合式（2）和式（5）得，于是有，在ω 较高前提下最终可得

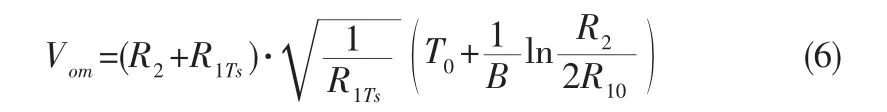
采用热敏电阻作为时变电阻和采用场效应管构成时变电阻具有相同的优点，即一旦振荡电路达到稳定，则负反馈系数Fv-不再改变。

2.3 二极管稳幅式

对图3(a)所示电路而言，由于输出电压vo(t)是正弦电压，故稳幅二极管D1或D2的导通阻值始终是随时间变化的，换言之，D1或D2的直流电阻和交流电阻应分别记为rD(vo(t), t)和rd(vo(t), t)。 随着vo(t)幅值vom的逐步增大和二极管自身温度的逐步升高， 导通二极管的直流电阻最小值rDmin和交流电阻最小值rdmin均将逐步减小（图3(b)、(c)），振荡趋于稳定。

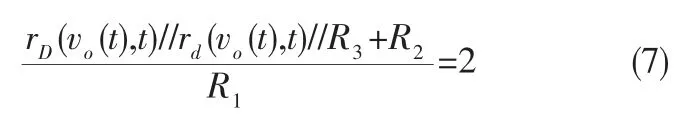
根据式（2）可得二极管稳幅RC 桥式正弦波振荡电路的稳态输出电压幅值Vom由决定。 但，因为二极管伏安特性的非线性，很难由式（7）给出V om 的解析表达式。文献[1]在假定二极管电压vD不变且已知的条件下，根据稳态下输出电压最大幅值时刻的KCL 方程

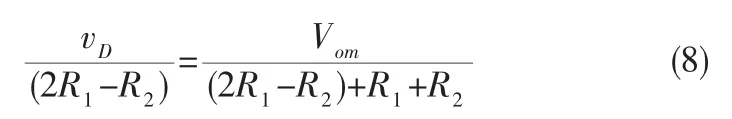
求取Vom。 文献[3]也是在同样的假定条件下给出图3 电路几个变型的近似计算公式。

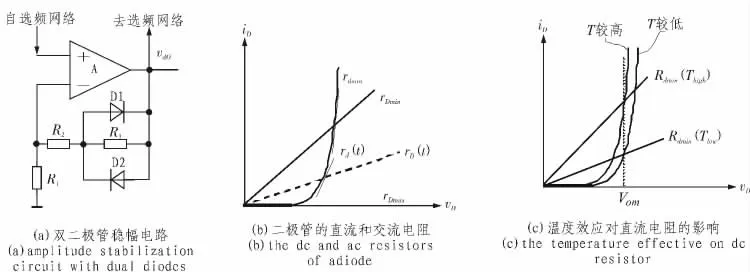
图3 双二极管稳幅电路及其电阻Fig. 3 Amplitude stabilization circuit using dual diodes and the resistor in it

从图3 可知，直流电阻rD是线性时变的，交流电阻rd是非线性时变的，且rD＞＞rd，其并联等效电阻的大小主要取决于rd。

2.4 决定电压幅值的元件特性参数

由式（2）和式（3）可知，决定场效应管负反馈式振荡电路输出电压幅值的， 是时变的场效应管漏源电阻的非线性参数VP和IDSS。 由式（5）和式（6）可知，决定热敏电阻负反馈式振荡电路输出电压幅值的，是时变的热敏电阻的非线性参数B、R10和T0。 由式（7）和式（8）可知，决定双二极管负反馈式振荡电路输出电压幅值的， 是时变的二极管电阻的非线性伏安特性参数。

3 虚拟实验验证

本节用仿真软件Multisim 12.0 以二极管稳幅RC 桥式振荡电路为对象进行虚拟实验，以验证时变/非线性电阻特性对RC 振荡电路过程影响的有关结论。 实验选用两种不同二极管进行。

实验电路如图4 所示， 表1 为电路元件参数和相应实验数据。 图5 证实本文“暂态时间和稳态幅值均与Fv－(0)和Fv－(·)有关”的结论。图6 清楚地显示了运放两个输入端的电压从起振时不相等到稳定振荡时相等的整个过程， 验证了本文关于“RC 桥式振荡电路稳定的过程是正反馈选频电路和负反馈电阻分压电路从不平衡到平衡的过程”。

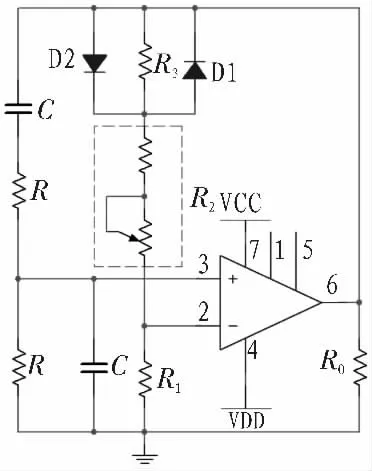
图4 虚拟实验用二极管稳幅电路Fig.4 Amplitude stabilization circuit with diodes for virtual experiment

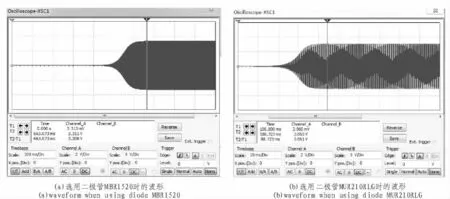
图5 输出电压在负反馈电路不同电阻分压比下的波形Fig. 5 Waveforms of output voltage when feedback circuit with different ratios of resistances

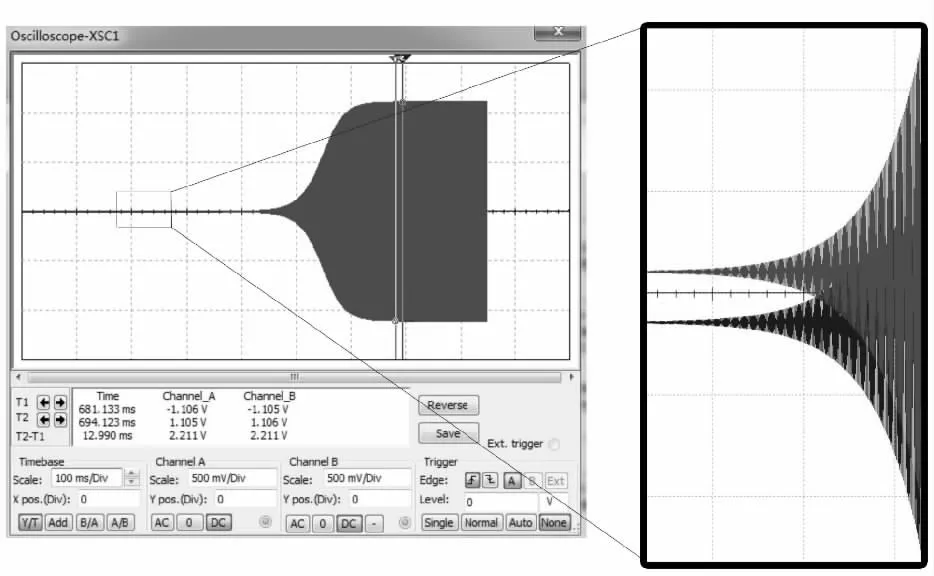
图6 运放同相输入端和反相输入端的电压波形Fig. 6 Waveforms of input voltages of OpAmp at positive terminal and negative terminal

表1 中输出电压幅值的实测值Vom和按式（7）计算值之 间的相对误差是足够小的。

表1 二极管稳幅振荡电路虚拟实验相关数据Tab. 1 Data from the virtual experiment on Wien-bridge using diodes to stabilize amplitude

4 结束语

本文的研究视角及出发点在以下两点上与现有文献有所不同：

1)从RC 桥式振荡电路结构存在的正反馈和负反馈回路视角出发， 在两个反馈从不平衡到平衡的过程中观察分析电路的起振和稳定；

2)指出RC 桥式振荡电路的稳幅过程是负反馈回路中电阻的时变性和/或非线性作用的结果，而非仅仅由电阻非线性特性的作用。

本文所得结论和定量结果有：

1)RC 桥式振荡电路正弦稳态电压的幅值取决于负反馈回路系数的时间函数Fv-(·)和其初始值Fv-(0)；

2)RC 桥式振荡电路稳定的过程就是正反馈选频电路和负反馈电阻分压电路从不相等到相等的平衡过程；

[1] 高燕梅，王丽.基于PSPICE的振荡器起振特性的仿真研究[J].实验技术与管理，2007，24（2）：91-93.

GAO Yan -mei, WANG Li. Study on simulation en -oscillating characteristics of LC oscillator based on PSPICE[J].Experiment technology and management, 2007, 24(2):91-93.

[2] 陈大钦.电子技术基础模拟部分习题全解[M].北京：高等教育出版社，2006.

[3] Guillermo Gonzalez. Foundations of oscillator circuit design[M]. Gale: Book News,Inc.,2007.

[4] 任骏原.RC桥式正弦波振荡电路的输出幅值分析[J].电子设计工程，2013，21（14）：107-108，110.

REN Jun -yuan. Study on the amplitude of RC -bridge oscillator [J]. Electronic Design Engineering, 2013, 21(14):107-108,110.

[5] 康华光主编.电子技术基础模拟部分[M].5版.北京：高等教育出版社，2006.

[6] 童诗白.模拟电子技术基础[M].2版.北京：高等教育出版社,1988.