基于峰值法的巨型框架结构试验模态分析

吴　明，杨永华，陈　东

(1. 合肥工业大学 土木与水利工程学院, 安徽 合肥 230009；2. 安徽建筑大学 土木工程学院, 安徽 合肥 230601；3. 上海师范大学 建筑工程学院, 上海 201400)

基于峰值法的巨型框架结构试验模态分析

吴明1, 2，杨永华3，陈东2

(1. 合肥工业大学 土木与水利工程学院, 安徽 合肥 230009；2. 安徽建筑大学 土木工程学院, 安徽 合肥 230601；3. 上海师范大学 建筑工程学院, 上海 201400)

基于一55层巨型框架结构振动台试验模型，给出了相似关系、模型周期、试验测点布置及试验加载制度，利用试验采集的数据，应用峰值法得到不同水准地震作用下试验模型的自振频率和振型.分析结果表明，随着地震动峰值的提高，结构自振频率明显下降，刚度降低，结构处于塑性工作状态；在弹性阶段的1阶振型呈弯剪型，在塑性阶段结构变形剪切型特征愈发明显.

巨型框架; 模态分析; 峰值法; 振动台试验

近年来，超高层建筑数量在国内不断增加，成为各大城市的地标性建筑.巨型框架结构传力明确、功能齐全、整体刚度大，因此被广泛应用于超高层建筑.由于其独特的传力特性[1-3]，巨型框架结构的动力模态与普通框架、剪力墙和框剪结构具有不同的特点.目前，现有的巨型框架结构模态分析主要针对数值模型进行研究，基于巨型框架振动台试验的模态分析较少.本文基于一高度为8.04 m的巨型框架结构的振动台试验结果，采用频域识别的峰值法进行结构模态的参数识别分析.

1　模型简介

巨型框架结构振动台试验模型共55层，其中50个普通框架层，第11， 22， 33， 44， 55层为巨型框架层，模型总高8.04 m，材料采用微粒混凝土．模型尺寸：平面尺寸为1.588 m×1.468 m,普通层和巨型层的层高分别为0.144和0.168 m，普通层和巨型层的楼板厚度分别为8和10 mm，整体模型如图1所示.

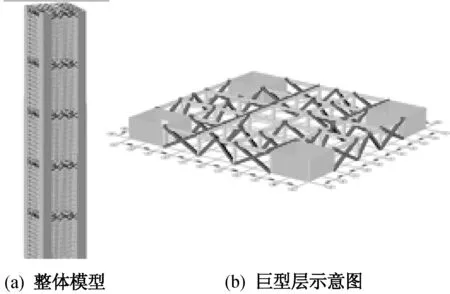
图1　试验模型Fig.1　Test model

试验模型长度相似系数Sl取1/25,同时根据混凝土试块材性试验得到混凝土平均弹性模量相似系数为0.35，材料应力相似系数取Sσ=0.35，加速度相似系数取Sa=4．基于Sl，Sσ和Sa这3个相似系数，根据似量纲分析法[4-5]确定其他相似关系.表1列出了模型各物理量及其相似系数，表2中列出了原型周期和根据相似关系计算得到的模型周期.

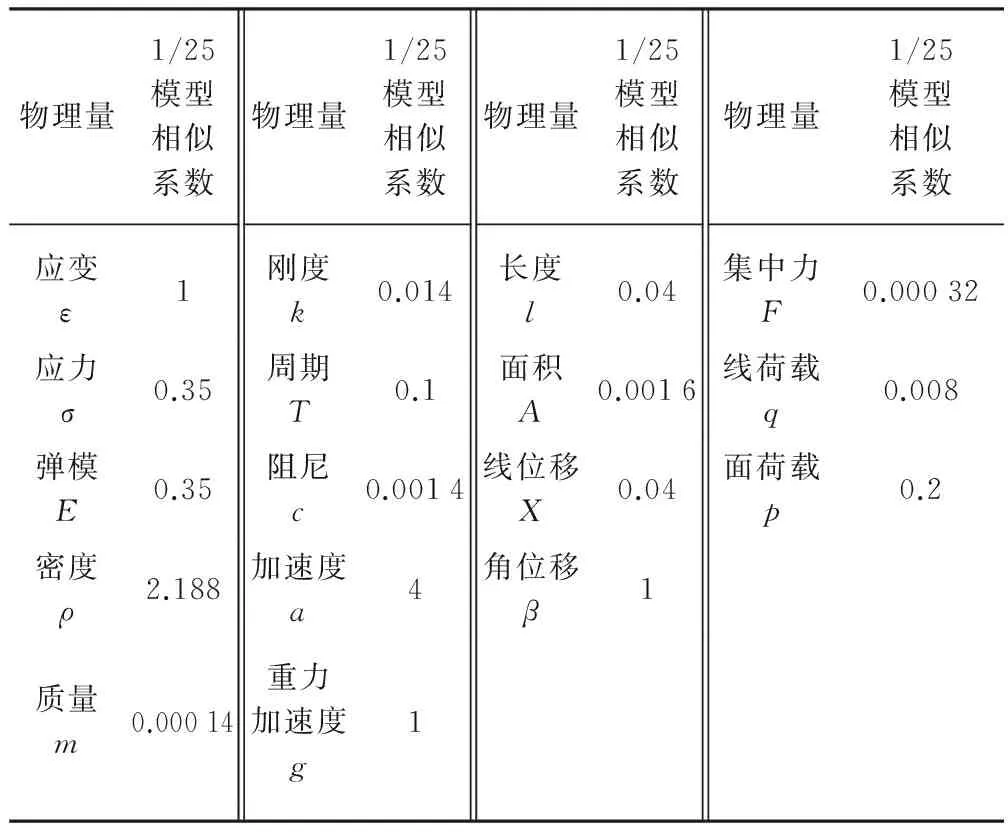
表1　模型各物理量的相似系数Table 1　Coefficient of physical quantities of model

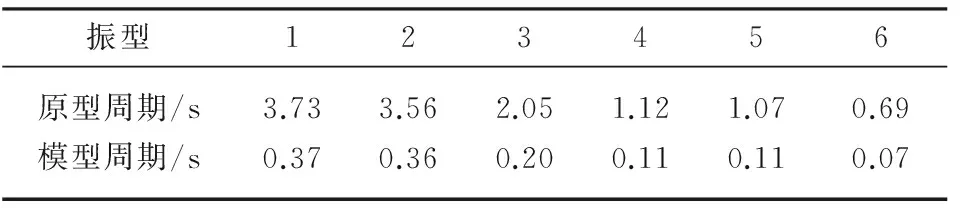
表2　原型及模型周期表Table 2　Periods of practical and testing model

2　试验测点布置及试验加载制度

模型加载时所采用的地震动为El Centro地震动、Chichi地震动、人工地震动、汶川地震动，具体加载制度及测点布置可参照文献[6]，为了得到结构的动力特性，在一些关键部位布置了加速度传感器，如表3所示.

表3　加速度传感器布置位置Table 3　Positions of acceleration sensors

3　模态分析

3.1白噪声加载

为了得到模型结构的频率、振型，试验利用白噪声对模型结构进行了扫频，白噪声的峰值加速度为0.07g，g为重力加速度，1g=9.8 m/s2，白噪声加载工况如表4所示．

表4　白噪声加载Table 4　White noise loading

3.2峰值法

峰值法基于频域对结构模态进行分析.当激励频率在结构自振频率附近时，频响函数出现峰值，即可通过峰值对特征频率进行估计.

结构的动力特性方程为

(1)

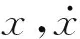
当输入信号u(t)为随机激励时，可利用信号的统计特性来表示u(t)的特征.随机激励u(t)的自相关函数，其中，E为数学期望，δ(τ)为单位脉冲函数，τ为任一时刻，Ru为一常数.

对随机过程的u(t)自相关函数进行傅里叶变换，得到其自功率谱密度函数Suu(ω)为

(2)

式中：ω为离散频率.

当已知输入u(t)时，频响函数和功率谱的关系为

Syy(ω)=H(ω)*Suu(ω)H(ω)

(3)

式中：Syy(ω)为响应的自功率谱密度函数；H(ω)为频率响应函数；右上角的*表示复共轭．

理想白噪声为一平稳随机过程，当其功率谱密度在某一个有限频率范围内均匀分布，而在此范围外为零，则称这个过程为带限白噪声.带限白噪声又可分为低通型和带通型.

(4)

式中：S0为一常数；A为截止频率.

带通型带限白噪声的功率谱密度满足

(5)

式中：B为通带宽度；ω0为中心频率.

由式(4)和(5)可知，白噪声的功率谱密度为非零常数，则式(3)即为

Syy(ω)=H(ω)*Sx(ω)H(ω)

(6)

对于有多个数据采集通道的系统而言，多个数据采集通道就有多个功率谱，为了包含所有测点的功率谱密度信息，可利用平均正则化功率谱密度(GANPSD)来选取峰值，进行频率识别[7].

(7)

式中：fk为第k个离散频率；GPSDi为第i个测点的功率谱密度函数;n为总的离散频率个数；l为测点个数．

不同工况后的测点功率谱密度函数如图2所示．由图2可知，功率谱峰值明显.对比不同工况的功率谱密度函数图，可看出结构频率发生了一定降低，表明结构受到了一定损伤而发生刚度下降．通过峰值法分析得到不同水准地震作用下试验模型的自振频率如表5所示.

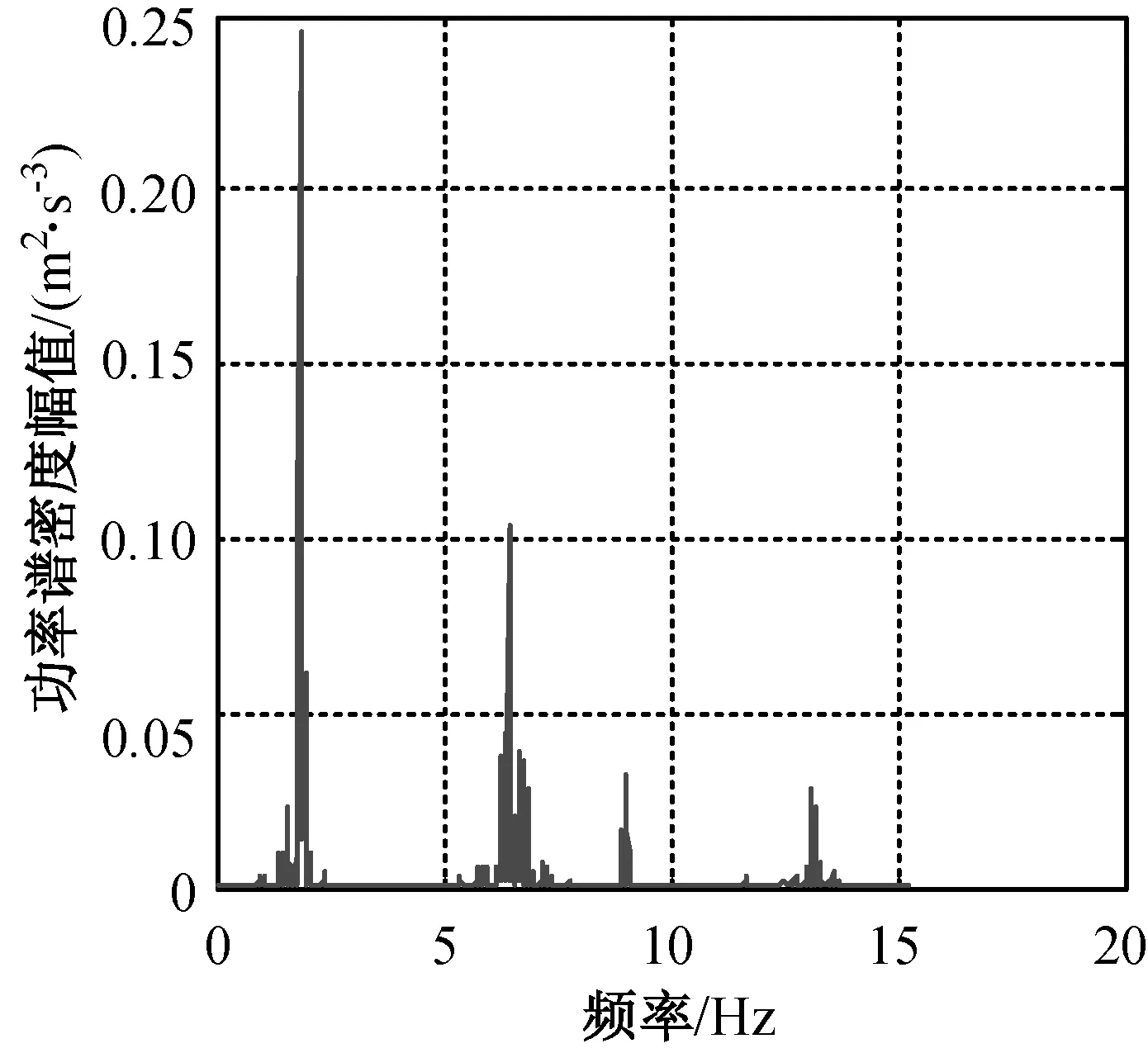
(a) 1WN

(b) 4WN

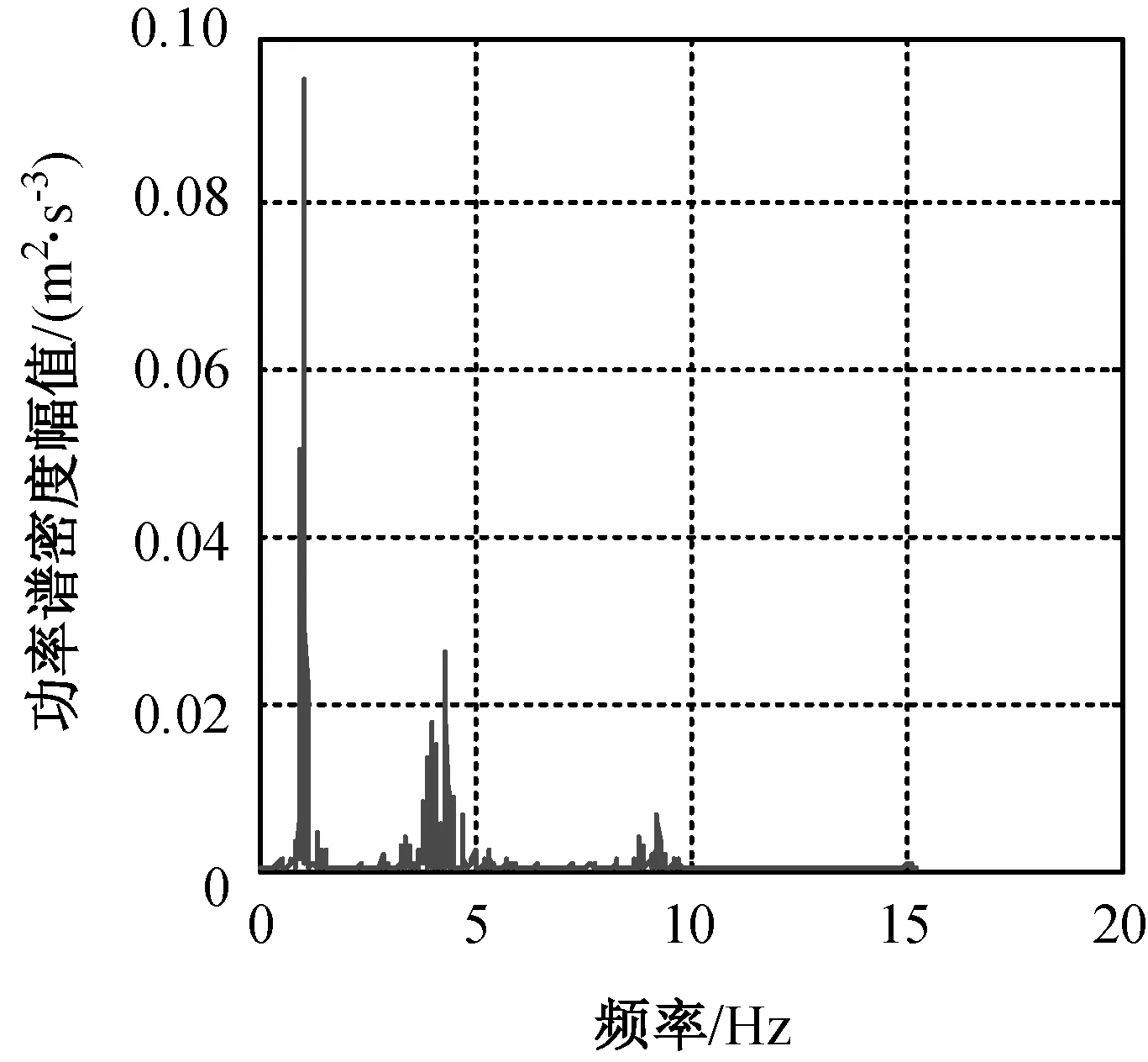
(c) 5WN

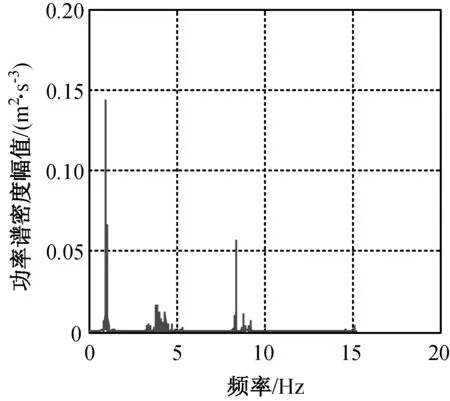
(d) 7WN图2　不同工况后的测点功率谱密度函数Fig.2　Power spectrum density functions of measure points after different load cases

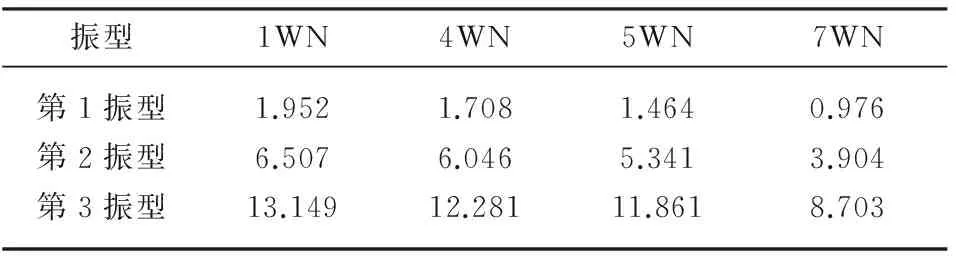
表5　不同工况后的自振频率Table 5　Natural vibration frequencies after different load cases Hz

试验过程中，在7度基本地震动加载前，模型表面均未发现明显的可见裂缝.由表5可看出，在7度罕遇地震作用后，结构基本频率下降了25%，台面极值地震作用后结构基本频率下降了50%，表明了台面极值地震作用后结构的自振频率下降非常严重，说明模型结构刚度下降,结构已处于塑性工作阶段.模型在各个工况后的振型如图3所示.

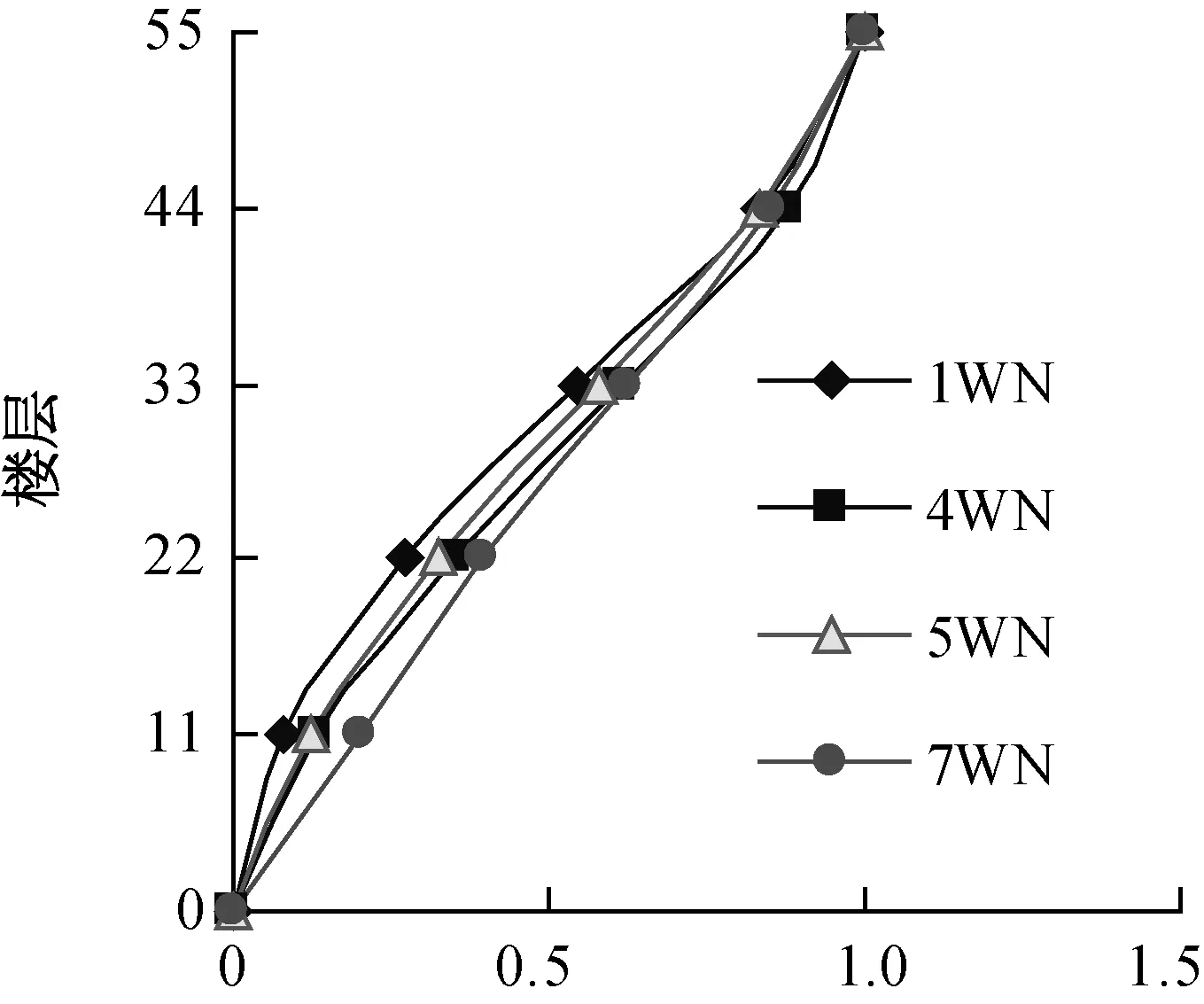
(a) 第1振型

(b) 第2振型图3　各个工况后的模型振型Fig.3　Model vibration modes after each load case

模型结构在单向地震动作用下的低阶振型的振动形态主要为平动.由图3(a)第1振型曲线的变化来看，加载前即弹性阶段振型呈现出明显的弯剪型特点，7度基本地震动加载后结构振型的剪切型特征愈发明显，这是由于随着加载的持续进行，结构发生损伤，次框架对主框架的约束作用不断降低.另外由图3(b)可看出，各种工况下的2阶振型变化不明显.

4　结　语

本文基于巨型框架结构的振动台试验数据，应用峰值法对模型结构进行参数识别和模态分析，得出以下主要结论.

(1) 7度基本地震输入后，振型及频率未明显变化，模型结构刚度变化不大；7度罕遇地震波输入后，结构的自振频率下降明显，表明模型结构处于塑性工作阶段.

(2) 模型结构在弹性阶段的1阶振型呈弯剪型，在塑性阶段由于结构的刚度降低，结构变形剪切型特征明显，在结构设计中应该充分考虑此种现象，构建合理的本构关系.

[1] 张富林,周健,项玉珍,等.上海陆家嘴金融贸易区X2地块南北塔楼结构设计与研究[J].建筑结构学报,2009,30(S1):15-16.

[2] 邹昀,吕西林.超高层巨型结构振动特性研究[J].世界地震工程,2007,23(2): 125-126.

[3] 杨航,陈麟,周云.巨型混合框架-核心筒结构的性能分析[J].工业建筑,2011,41(3): 63-64.

[4] 邹昀,吕西林,卢文胜，等.上海环球金融中心大厦整体结构振动台试验设计[J].地工程与工程振动,2005,25(4):54-59.

[5] 吕西林.复杂高层建筑结构抗震理论与应用[M].北京:科学出版社,2007:201-284.

[6] 吴明,叶献国,蒋庆，等.巨型框架振动台试验设计[J].工业建筑,2013,43(6):47-51.

[7] 禹丹江.土木工程结构模态参数识别[D].福州:福州大学土木与建筑工程学院,2006: 20-25.

Test Modal Analysis of Mega Frame Structures Based on Peak Method

WUMing1, 2,YANGYong-hua3,CHENDong2

(1. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China;2. Civil Engineering School, Anhui Jianzhu University, Hefei 230601, China;3. College of Civil Engineering, Shanghai Normal University, Shanghai 201400, China)

Based on the shaking table test for a 55-storey mega frame structure, similarity relation, model period, arrangement of measuring points, and loading system for the test model are presented. Natural frequencies and vibration modes of the test model under different ground motion are obtained by using the peak method with the test data. The analysis results show that the structural frequencies and stiffness reduce with the increase of the peak of ground motion. The first order mode shape is shear-flexural type in the elastic stage, and shear characteristics is apparent in the plastic stage.

mega frame; modal analysis; peak method; shaking table test

1671-0444(2015)04-0509-04

2015-04-05

国家自然科学基金重大研究计划资助项目(90715016)；土木工程防灾国家重点实验室开放课题基金资助项目(SLDRCE08-HZ-01)

吴明(1969—)，男，安徽芜湖人，讲师，博士研究生，研究方向为结构工程.E-mail:frank_wucn@126.com

P 315.8

A