一种基于Petri网模型的数控系统的分析与在线实时故障诊断方法

田仁铁，杨建国

(1.平壤机械大学 机械制造工程学院,平壤 朝鲜；2. 东华大学 机械工程学院,上海 201620)

一种基于Petri网模型的数控系统的分析与在线实时故障诊断方法

田仁铁1, 2，杨建国2

(1.平壤机械大学 机械制造工程学院,平壤 朝鲜；2. 东华大学 机械工程学院,上海 201620)

以数控镗床为对象，提出了一种基于Petri网的数控系统的建模、分析以及故障诊断方法.为了保证故障诊断的实时性和正确性，用Petri网构建了HNC-22MD镗床数控系统的分析模型，并对系统的可达性、有界性、活性等进行了分析，定义了标识矩阵，以此实现镗床数控系统的在线实时故障诊断.实验结果表明，这种方法可充分反映镗床数控系统的控制和信息流程，为数控镗床的高效、可靠和稳定运行提供了理论基础.

Petri网；建模；模型分析；故障诊断；数控镗床

Petri网(PN)是分布式和并行系统建模与分析的有效工具，其广泛应用于机械制造和故障诊断领域[1-6]. 文献[1]用实时模糊Petri网实现了制造系统的预测故障诊断，而文献[2]提出了Petri网故障模型的识别和综合方法.文献[3-8]基于Petri网提出了提高机械加工质量和改善制造调度的方法.文献[9]研究了基于矩阵及其运算的推理方法，实现了基于Petri网的远程智能故障诊断系统. 文献[10]提出了合成模糊产生式规则的Petri网模型,并利用机车的模糊Petri网模型进行故障诊断分析. 文献[11]建立了数控机床生产中所面临的故障诊断的Petri 网模型, 并分析了故障的传播机理. 文献[12]采用基于置信规则库的方法对数控铣床伺服系统的工作台进行了故障诊断. 文献[13]建立了针对车床转塔刀架故障的Petri 网诊断模型. 文献[14]给出数控机床主轴的Petri 网模型，找到引起主轴故障的根本原因.当普通机床改成数控机床时，不仅要检查电路设计、软件设计以及机械设计的正确性，而且需要考虑数控(CNC)系统会发生的所有事件、操作和控制信息流程的相互关系，另外，需要检测和诊断在改造的数控机床的运行当中会遇到的任何故障问题.本文介绍了一种基于Petri网的数控系统的建模、分析和在线实时故障诊断方法，从而确保改造设计的正确性和系统运行的可靠性及稳定性.

1　基于Petri的镗床数控系统的建模

1.1基本标识Petri网概述

基本标识Petri网结构是由五要元描述的有向图：

PN={PNS, m}={P,T,I,O,m0}

(1)

其中：PNS={P, T, I, O}为PN结构；P={p1,p2, …,ph}是库所的有限集合，h为库所的个数；T={t1,t2, …,tg}为变迁的有限集合，g为变迁的个数，P∩T=∅；I:P×T→N为输入函数，它定义了从P到T的有向弧的重复数或权的集合，N={0, 1, …}为非负整数集；O:T×P→N为输出函数，其定义了从T到P的有向弧的重复数或权的集合；m:P→N为标识Petri网的标识，它为一列向量，其第i个元素表示第i个库所中的托肯(token)数目.特别地，m0为初始标识，表示离散事件系统的初始状态.

在基本标识Petri网中，库所表示数控系统的局部状态(如自动运行、刀具转换等)，变迁表示其所有可能的事件(如按下急停按钮、碰到一个极限开关等).

1.2基于基本标识Petri网的数控系统的建模

通过对武汉华中数控股份有限公司的HNC-22MD型数控装置的研究分析，用基本标识Petri网建立了数控系统的模型.先建立整个数控系统的模型，然后按照运行方式建立每个子系统的模型.整个数控系统的PN模型如图1所示. 在PN模型中, PN的基本库所以圆表示；PN的子模型以矩形表示，子模型也是一个由库所和变迁组成的PN；变迁以粗实线段表示；托肯以库所中黑色圆点表示.

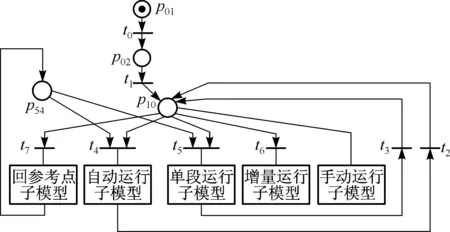
p01—机床上电；p02—伺服准备完毕；p10—手动运行方式；p54—回零完毕；t0—松开急停按钮；t1，t2和t3—按手动运行方式按钮；t4—按自动运行方式按钮；t5—按单段运行方式按钮；t6—按增量进给方式按钮；t7—按回参考点方式按钮图1　整个数控系统的PN模型Fig.1　PN model of the CNC system

HNC-22MD型数控装置具有5个运行方式：自动运行方式、单段运行方式、手动运行方式、增量进给方式以及回参考点方式.通电后系统默认进入手动运行方式.

按照运行方式，建立每个子系统的模型.自动运行方式是数控镗床的基本运行方式(本文仅以自动运行方式为例介绍)，包括自动加工方式和程序校验方式两种运行方式.自动运行方式的子PN模型如图2所示.

p20—自动运行方式；p21—等待执行加工程序；p22—在自动加工方式下等待；p23—在程序校验方式下等待；p24—正在自动加工中；p25—正在校验程序中；p26—自动加工暂停；p27—校验暂停；p28—自动运行完毕；t21—选择加工程序；t22—选择自动加工方式；t23—选择程序校验方式；t24—按循环启动按钮(开始自动加工)；t25—按循环启动按钮(开始程序校验)；t26—按进给保持按钮(暂停自动加工)；t27—按进给保持按钮(暂停程序校验)；t28和t29—最后段执行完毕；t126—按循环启动按钮(继续自动加工)；t127—按循环启动按钮(继续程序校验)；t128—停止自动加工；t129—停止程序校验图2　自动运行方式的子PN模型Fig.2　Submodel of PN for the automatic operation mode

2　镗床数控系统的PN模型分析

2.1PN模型分析方法

PN网模型的特性可以准确地反映系统的动态特性和静态特性.通过分析系统的PN模型,可以保证系统设计的正确性与安全性.

系统的PN模型特性包括状态的可达性、库所的有界性、变迁的活性与锁死性等.可达性用来描述若系统按照一定的轨迹运行，则系统是否能够实现一定的状态或者不出现不期望的状态.PN的有界性是检查被PN所描述的系统是否存在溢出的有效尺度.当库所用于描述一个操作时，该库所的安全性能够确保不会重复启动某一正在进行的操作.PN的活性意味着在任意从初始标识m0可达的目标标识mr下，总可以通过逐步激发某变迁序列来激发任意变迁.因此，若PN模型是活的，则其不存在锁死.

PN的分析方法主要依赖于可达树、基于矩阵方法与状态方程等.基于矩阵方法是一种基于矩阵线性代数的方法，其优点是依据简单的线性代数方程，就能正规地确定PN性能.因此，本文采用基于矩阵方法进行镗床数控系统的PN模型分析.在PN中，可用I与O这两个矩阵表示库所与变迁之间的关系，两者之差O-I为关联矩阵C.基于关联矩阵C，可以分析PN的某些性能.

若从初始标识m0开始激发一个变迁序列产生标识mr，则称mr是从m0可达的.若从m0开始只要激发一个变迁即可产生mr，则称mr是从m0立即可达的.

若具有初始标识m0的PN可达到目标标识mr，那么它要满足：

mr=m0+C uk

(2)

其中：uk为一个(l×1)激发向量,该向量的第i个元素对应着变迁ti出现的次数ni.一般地，uk=(n1,n2,…，nl)T.式(2)为Petri网的状态方程.

由于所有库所中的托肯数是非负的，因此合法的运行(激发使能的变迁)将保证：

m0+C uk≥0，对于所有k≥0

(3)

式(3)可用于检验在m0下激发某一变迁序列是否合法.

若只要存在一个(n×1)正实数向量x，使得xTC≤0，则PN是结构上有界的.这里x称为P不变量，它是个非负整数向量.

2.2镗床数控系统的PN模型分析

根据2.1节的方法，对镗床数控系统PN模型进行分析.

在自动运行方式下，自动加工方式的库所集和变迁集为

P={p20, p21, p22, p24, p26, p28}

T={t21, t22, t24, t26, t126, t128, t28}

输入函数和输出函数可以用矩阵表示为

而关联矩阵C为

在自动加工方式PN模型中初始标识m0和目标标识mr为

m0=(1 0 0 0 0 0)T

mr=(0 0 0 0 0 1)Τ

根据式(2)求激发向量uk，则得到：

于是目标标识mr是从初始标识m0可达的，而自动加工方式PN模型是活的,并且

m0+ C uk=(000001)Τ

满足m0+C uk≥0，因此在m0下激发变迁序列uk是合法的.

求解线性方程xTC=0，则获得自动加工方式PN模型的P不变量：

x=(111111)Τ

显然，PN被正的P不变量覆盖，因此PN是有界的，由此能确定设计的自动运行方式安全、可达、正确.这意味着数控系统的自动运行是能够实现的，而且不期望的状态不会出现，也说明数控系统不存在溢出和锁死，且确保不会重复启动正在进行的一项操作.

3　用PN模型的镗床数控系统的在线实时故障诊断

3.1用PN标识矩阵的故障诊断方法

结合第1节的自动运行方式的子PN模型及第2节的矩阵分析, 可知镗床数控系统的PN模型描述数控系统的控制流程和信息流程.自动运行方式子PN模型的可达图如图3所示.

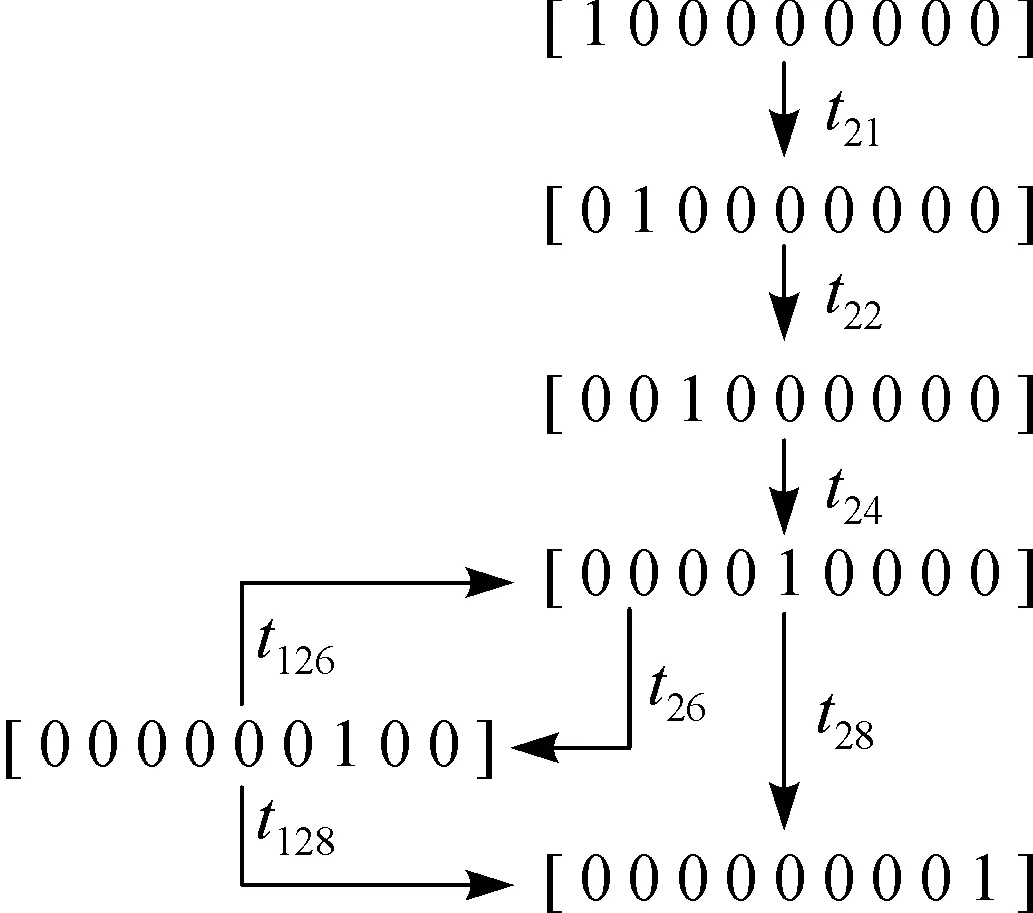
(a) 自动加工方式

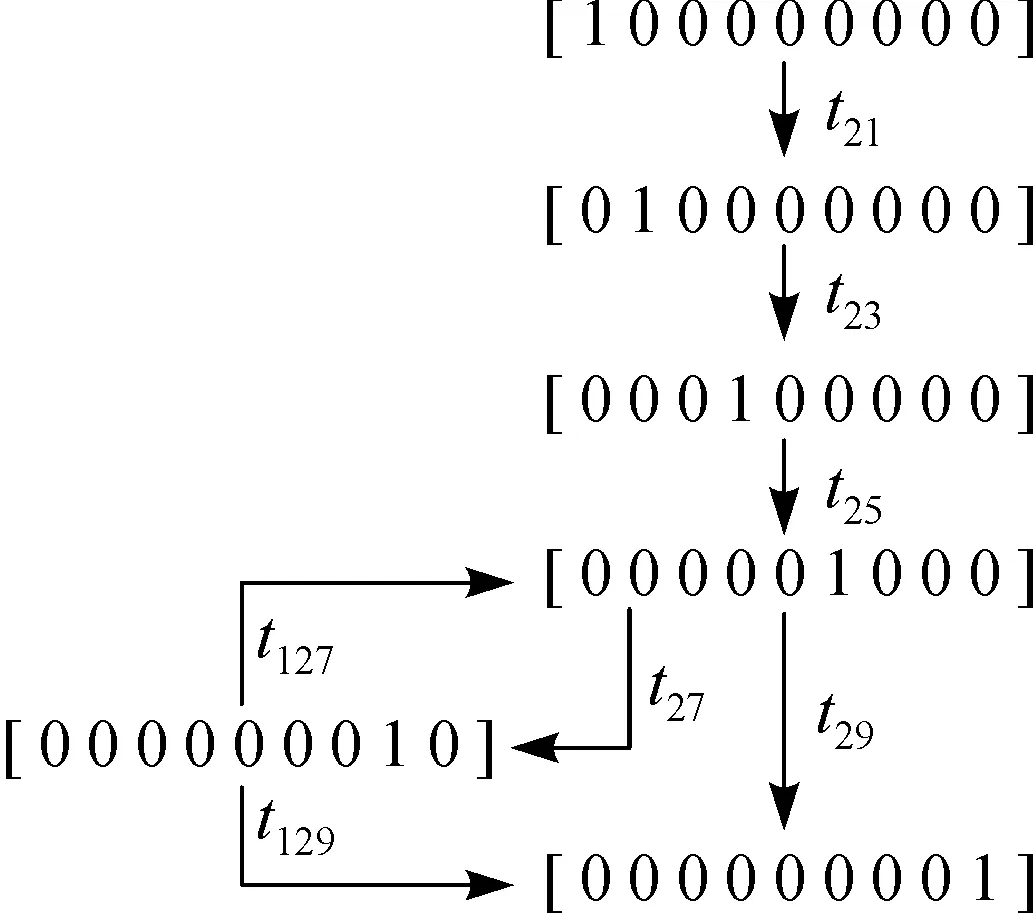
(b) 程序校验方式图3　自动运行方式子PN模型的可达图Fig.3　Reachability graph of the submodel PN for automatic operation mode

图3说明自动运行方式子PN模型有两个可达图，对应于自动加工方式和程序校验方式，且显示标识的流动过程即信息和控制的流程.因此，用这些PN模型获得数控系统在正常运行情况下的状态数据，与系统的现有状态相比，能在线实时检查系统的故障.

在PN模型中，系统的状态用标识表示，因此，状态的变化过程即为标识的变化过程，从而用标识能检查数控系统的故障.为了便于故障检查引入标识矩阵的概念.

定义由PN的标识mr排成的m×n矩阵

(4)

式(4)称为标识矩阵，其中r=1, 2, …，m;k=1, 2, …，n.mr(pk)是第r系统局部状态的第k库所中所包含的托肯数目，即标识矩阵的每行描述系统在正常运行情况下的一个局部状态.

因为PN模型按照数控系统的运行方式而建立，所以标识矩阵也按照运行方式来构成.自动加工方式的标识矩阵为

(5)

自动加工方式可能出现3种运行方式：经过暂停完毕加工，此时标识矩阵与式(5)一样；不经过暂停完毕加工，此时标识矩阵是式(5)中排除第5行和第6行的矩阵；加工当中停止加工，此时标识矩阵是式(5)中排除第6行的矩阵.每个运行方式的标识矩阵存放到数控装置的内存.

3.2镗床数控系统在线实时故障诊断的实现

为便于二次开发以及增加其他功能，HNC-22MD型数控装置的内嵌式PLC采用Borland C++3.1编辑PLC程序.PLC程序由函数reset()、plc1()和plc2()组成，其中函数plc1()和plc2()的扫描时间由宏plc1_time1和plc2_time给定.故障诊断程序diagno_pro()属于函数plc2().

镗床数控系统故障检测和诊断流程如图4所示.在图4中，诊断数据库是根据数控系统的原理分析和运行经验建立的，用IF-THEN形式的产生式规则构成.采取HNC-22MD提供的宏(如 #define message_no() (G_ui[])、#define axis_stat(x) (F_ui[(x)*10])等)实现诊断结果显示、运行方式和系统状态.

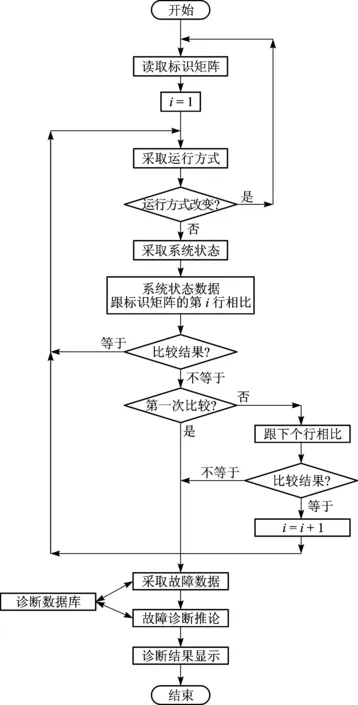
图4　镗床数控系统故障检测和诊断流程Fig.4　Fault detection and diagnosis process for boring machine CNC system

3.3镗床数控系统在线实时故障诊断实例

在正常运行状态下回参考点方式的标识矩阵为

(6)

为了验证故障诊断的可行性和正确性，进行如下的实验.先断开一个y轴参考点开关的端子线，然后启动数控系统，令系统运行回参考点方式.完成z轴回参考点后，系统进行y轴回参考点.因为断开一个y轴参考点开关的端子线，所以不能完成y轴回参考点，却碰到y轴正极限开关，系统处于警报和停止状态.此时标识矩阵变为

(7)

故障诊断程序按照图4 的流程运行，发现M的第5行跟M0的第5行不同，且判断在y轴回参考点当中发生异常状态：

switch(mode_sel) //采取运行模式

{

caseMODE_REF_RETURN: //回参考点模式

……

mark_matrix();//采取和处理标识矩阵的函数

……

if((*axis_stat(1) & AX_HOME_GOING) == 1) // 如果y轴正在回零

{

……

if(((X[1]&0x04)==0)&&((R[11]& 0x04)==0)&&((R[21]& 0x04)==0))!=0))

//如果碰到y轴正极限开关(y轴正极限开关输入点为X1.2)

{

……

diag_infer();//诊断推理函数

……

}}}

执行诊断推理函数得到故障信息号12.然后系统使用宏*message_no()=12，令数控系统界面显示如下的诊断信息：

“在y轴回参考点当中发生行程超过；y轴参考点开关故障或者PLC输入点连接不好”

这与实际故障原因一样，从而验证本文故障诊断可行、正确.

4　结　语

为了确保镗床数控化技术改造的科学性，本文建立了数控系统PN模型，并用不变量方法分析了其可达性、有界性、活性等动态特性和静态特性.在数控系统实现之前能够预测该系统的可达性、活性和安全性等，而且能够修改发生的错误.同时为了减少数控镗床的维修时间和提高镗床的可用性，本文提出了基于Petri网模型的数控系统的在线实时故障诊断方法.因为数控系统的资源有限，所以根据数控系统的Petri网模型定义了新的标识矩阵，然后以标识矩阵为参考数据实现镗床数控系统的在线实时故障诊断.这有效利用了数控装置的资源，以便实现在线实时故障诊断功能.

[1] WU Z H, HSIEH S J. A realti-me fuzzy Petri net diagnoser for detecting progressive faults in PLC based discrete manufacturing system[J]. International Journal of Advanced Manufacturing Technology, 2011, 61(1/2/3/4): 405-421.

[2] CABASINO M P, GIUA A, HADJICOSTIS C N, et al. Fault model identification and synthesis in Petri nets[J]. Discrete Event Dynamic System, 2015, 25(3): 419-440.

[3] KASIROLVALAD Z, JAHED MOTLAGH M R, SHADMANI M A. An intelligent modeling system to improve the machining process quality in CNC machine tools using adaptive fuzzy Petri nets[J]. International Journal of Advanced Manufacturing Technology, 2006, 29(9): 1050-1061.

[4] BASILE F,CHIACCHIO P, MAZZOCCA N,et al. Modeling and logic controller specification of flexible manufacturing systems using behavioral traces and Petri net building blocks[J]. Journal of Intelligent Manufacturing,2004,15(3):351-371.

[5] HU H S, LI Z W. Modeling and scheduling for manufacturing grid workflows using timed Petri nets[J]. International Journal of Advanced Manufacturing Technology， 2008, 42(5): 553-568.

[6] LÜ Y Q, LEE C K M, CHAN H K, et al. RFID-based colored Petri net applied for quality monitoring in manufacturing system[J].International Journal of Advanced Manufacturing Technology, 2012, 60(9): 225-236.

[7] 蔡热文.基于面向方面的时间Petri网的实时信息物理系统的建模[D].广州：广东工业大学计算机学院，2012：14-22.

[8] 史晓娟，王小椿.智能化数控系统的建模分析[J].仪器仪表学报，2003，24(6):640-642.

[9] 熊伟.基于Petri网的远程智能故障诊断方法研究[D].北京：华北电力大学控制与计算机工程学院，2014：25-32.

[10] 张才炎.基于Petri网的机车故障诊断方法研究[D].长沙：中南大学机电工程学院，2010,12-28.

[11] 赵志刚，吕慧显，钱积新.基于Petri网的多轴机床故障诊断研究[J].机床与液压，2002(3):143-144,139.

[12] 张玉玲. 数控铣床伺服系统故障诊断与预报的研究 [D].长春：长春工业大学机电工程学院，2012：17-30.

[13] 牛同训,解先敏,王恩海.CB3463-1车床转塔刀架故障诊断Petri网模型研究[J].机床与液压, 2011，39(17):140-143.

[14] 申桂香，王志琼，张英芝，等.基于模糊Petri网的数控机床主轴故障诊断[J].制造技术与机床，2012(3):124-127.

An Analysis and Online Real-Time Fault Diagnosis Method of CNC System Based on Petri Net Model

TIANRen-tie1， 2,YANGJian-guo2

(1. College of Mechanical Manufacturing Engineering, Pyongyang Mechanical Engineering University，Pyongyang, DPR of Korea; 2.College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

For computer numerical control(CNC )boring, a method was proposed for model building，analysis and fault diagnosis based on Petri net. In order to ensure the real-time and correctness of fault diagnosis, analysis model of the HNC-22MD boring CNC system was constructed by using Petri net. Reachability, boundedness and activity of the system were analyzed. The mark matrix was defined and used to achieve an online real-time fault diagnosis of the boring CNC system. Experimental results show that this method can sufficiently reflect the control and information flow of the boring CNC system, it can provide a theoretical basis for efficient, reliable and stable operation of CNC boring machines.

Petri net； modeling； analysis of the model； fault diagnosis； computer numerical control boring

1671-0444(2015)04-0503-06

2015-03-30

田仁铁(1975—)，男，朝鲜人，副教授，硕士，研究方向为机械电子.E-mail:jicjkw728@163.com

杨建国(联系人)，男，教授，E-mail:jgyangm@dhu.edu.cn

TP 206+.3

A