无容量约束下工作量均衡的转运网络设计
李淑霞,方陈浩,吴一帆
(华东理工大学 商学院,上海 200237)
无容量约束下工作量均衡的转运网络设计
李淑霞,方陈浩,吴一帆
(华东理工大学 商学院,上海 200237)
在无容量约束条件下的转运网络设计的基础上考虑工作量均衡问题.首先,以总运输成本最小化为目标构建单一分配模式下的转运网络模型.其次,通过对初始转运网络增加转运中心数量并重新分配服务节点,尽可能地实现转运中心工作量的均衡,同时以工作量方差缩减程度判据确定转运中心数量.最后,采用Civil Aeronautics Board数据集进行算例分析.结果表明,不考虑容量约束时,转运贴现因子不影响转运选址,这由单一分配模式的特性所决定.另外,方差缩减程度判据是考虑工作量均衡的转运网络设计的重要依据.
转运网络设计;转运中心选址;工作量均衡;运输优化
现代物流发展越来越迅速,已朝着复杂网络化趋势不断发展.大到国家间的物流运输,小到区域、城市间的物流运输,几乎都通过一级、两级甚至多级的转运形式.特别是在我国东部沿海地区,转运中心的建设数量占全国总量的78%,其选址以及运输网络设计对提高运输效率和控制成本产生了非常重要的影响,因此,转运网络的优化设计对于物流运输而言具有重要的研究意义.
在转运网络中,转运中心具有整理、转换和连接的功能.转运中心的具体位置分布、转运中心间的运输联系、非转运中心与转运中心的分配方式以及网络中流量的具体安排,直接影响着转运网络的运输效率和运输成本.自文献[1]首次提出转运中心选址问题至今,有关该领域内的研究成果层出不穷[2-10],涉及分配模式的选择、完全与非完全转运中心选址以及目标的选择等.就分配模式而言,可分为单一分配模式和复杂分配模式,不同分配模式下转运网络的设计已成功应用于航空等运输网络,较好地解决了运输和环境成本高、服务质量低等问题.对于是否属于完全转运中心选址,即由转运中心点构成的子网络是否属于完全图的情形,多数研究考虑的是完全转运中心选址问题,即任意两个转运中心间都存在转运中心弧.其中,文献[11]采用两阶段法研究了巴西航空市场的转运系统结构,以总成本最小化为目标分别选出小型、大型转运中心,评估了世界杯期间由于运输高峰而产生的额外客流对运输系统的影响.而对于非完全转运中心选址问题,文献[12-14]分别提出了p-均值问题、带有固定成本的转运中心选址问题、转运中心覆盖问题和p-转运中心网络设计问题,用算例证明了非完全转运中心能够以比完全转运中心更低的成本实现相同的服务质量.在目标选择方面,总成本最小化是各类转运网络设计问题的首要目标.当然,也有部分研究[15]针对现实问题的需求,在考虑成本最小化的基础上增加了服务水平、运输时间等目标,旨在实现成本与服务水平、运输时间的均衡.
然而,上述研究大多着眼于整体最优,而较少考虑每个转运中心的工作量情况.由于不考虑每个转运中心工作量的优化配置,有可能会出现某些转运中心超负荷运作的情形,从而导致转运中心内部操作成本增加、员工加班甚至“爆仓”等问题,最终不利于运输网络的可持续发展.因此,在不扩大转运中心规模的前提下,合理分配各转运中心服务的区域具有重要的研究意义.本文从每个转运中心工作量相对均衡的视角出发,考虑运输网络的优化设计问题,通过增加转运中心数量尽可能地均衡工作量,并以方差的变化作为评判标准,确定合适的转运中心及其流量分配,进而建立相应的运输网络.
1 模型建立
转运网络通过设置转运中心并采用大型运输工具实现运输,转运中心间的运输费用会有所降低.然而,基于总成本优化的考虑,决策者对于转运中心数量存在不同偏好,从而造成转运中心间运输量的不均衡,给部分转运中心带来很大的工作负担,不利于长远发展.因此,需要在转运网络设计的基础上综合考虑各个转运中心间工作量的均衡问题.
1.1符号定义及假设
α为转运中心之间的转运贴现因子;cij为节点i与节点j之间的单位运输费用;N为节点的集合,N=1, 2, …,n;p为转运中心的数量;fij为节点i与节点j之间的运输量;xik为二元决策变量,xik=1表示节点i分配给转运中心k,否则为0.
同时,根据问题的背景,给出如下假设:
(1) 运输工具的运输速度为恒定值,且以直线运输,不存在绕道的情况;
(2) 运输网络中的路径满足三角不等式.
1.2转运网络的工作量均衡
由于影响转运网络设计的因素有很多且关系复杂,这里不考虑除成本和工作量之外其他因素的影响,如运输时间、天气状况等.在转运网络中,节点间的运输通过一对转运中心来实现,且由于规模效应的作用,转运中心间的运输费用比一般两点间的运输费用低.引入转运贴现因子α(0<α<1),即如果运输从起点i到终点j,经过一对转运中心k和l,那么,相应的费用为cik+αck l+clj.
考虑含有n个节点的网络,在这n个节点中选取p个节点,作为网络的转运中心.以总运输成本最小化为目标函数,建立如下无容量约束的单一分配模型:
(1)
(2)
(3)
xik≤xkk
(4)
(5)
目标函数(1)表示总运输成本的最小化.约束条件(2)表示每一个节点只分配给一个转运中心;约束条件(3)表示建立p个转运中心;约束条件(4)表示节点能够分配给转运中心的前提条件是该转运中心已被建立;约束条件(5)为二元决策变量,表示节点是否分配给转运中心.
利用优化软件CPLEX求解上述模型,建立总成本最小化的初始转运网络,并分配转运中心所服务的节点.不难发现,转运中心的数量p取决于决策者的偏好,且该转运网络的建立与p的选择有直接联系.另一方面,p值过小可能带来转运中心的工作量不均衡,给实际运作带来若干问题.为此,这里提出方差缩减程度判据,在求得初始转运网络基础上,通过合理增加转运中心数量,并以总运输成本最小化为目标重新分配每个转运中心所服务的节点,进而实现工作量的均衡.
设dij为转运中心j所服务的节点i的运输量,di为节点i的初始运输量,则网络中所有节点的运输量总和为,各个转运中心所服务的运输量总和为,转运中心工作量的方差δ2表示为
(6)
(7)
(8)
ηp′p″=ηp0p′-ηp0p″≤η
(9)
通过上述方法,可以将工作强度高的转运中心服务的部分节点转移至工作强度低的转运中心进行服务,对其进行“减量”,从而得到了总成本相对较低、工作量相对均衡的转运网络设计,具体流程如图1所示.这样既有利于提高转运网络的整体运作效率,又符合运输行业内部可持续发展的要求.

图1 无容量约束下工作量均衡的转运网络设计流程Fig.1 Process of uncapacitated network design for flow equilibrium
2 算例分析
上述模型属于整数线性规划模型,可以利用优化软件CPLEX 12.6对其编程求解,其中,转运中心数量p由决策者确定.通过编程求解,可求出每个转运中心所服务的节点,并计算出各个转运中心的工作量情况.如果工作量相差不大,即表示所求的转运网络就是满意解;如果存在一个或者某几个转运中心的工作量明显比其他转运中心工作量大很多的情形,则考虑逐步增大p值,即增加转运中心的数量,重新分配服务节点并计算转运中心工作量的方差及其变化率,直至满足限定条件为止.
2.1转运贴现因子对最优选址的影响
采用著名的Civil Aeronautics Board(CAB)数据集对模型进行算例验证,并结合实际意义加以分析.CAB数据集是由M. E. O’Kelly提供的,其中包含了25个节点间的流量和运输成本数据,被广泛应用于转运中心选址问题的研究.由于原始数据相对比较大,考虑到使用原数据进行编程求解会使得最后结果十分庞大,不便于分析.因此,首先对原数据进行处理,将节点间流量的数据归一化,即令节点间的流量除以总流量后的值作为新的流量值,使得总流量值为1.根据模型,如果选择建立4个转运中心,即p=4,并且令转运中心之间的转运贴现因子α=0.5.结合CAB数据集用优化软件CPLEX 12.6编程求解,可以求得最小化的总运输成本为11957.4,相对应的转运中心为4, 12, 17, 24.逐步改变转运贴现因子的值,得到不同转运贴现因子下的最优选址和相应的总运输成本,如表1所示.

表1 不同转运贴现因子下的最优选址和相应的总运输成本Table 1 Optimal locations and total transportation costs under different discount factors
由表1可知,在单一分配模式下的无容量约束转运网络设计问题中,转运贴现因子仅会对总运输成本产生影响.这是因为单一分配模式侧重于确定非转运中心节点与转运中心的分配,而转运贴现因子则体现在转运中心间的运输过程中,表示在转运中心间用大型运输工具进行运输,能够降低单位运输成本.因而在单一分配模式条件下,不同转运贴现因子不会影响最优选址.
2.2转运中心工作量的均衡
不失一般性,以p=4,α=0.5情形下得到的网络作为初始网络,研究转运中心工作量的均衡问题,对应服务节点分配及每个转运中心的工作量则如表2所示.

表2 转运网络的具体节点分配及每个转运中心的工作量情况Table 2 Service nodes and total amount of flows through hubs
由表2可知,相较于其他两个转运中心而言,转运中心4和17所服务的节点数量较多,工作总量也近似于其他两个转运中心的总和,相差比较大.在规模固定的条件下,若能将转运中心4和17的部分服务节点分配给其他转运中心,就能对其适当“减压”,故要实现工作量的均衡,就需要增加转运中心的数量.


表3 不同m情形下的最优转运网络Table 3 Optimal hub networks with differentm
由表3可知,增加转运中心数量能够降低总运输成本,这是因为存在转运贴现因子.因此仅就总运输成本而言,转运中心数量越多越好.然而,考虑到在已经相对优化的转运网络中,建立更多的转运中心并不一定会对网络有更明显的改善.因此统计相应的方差δ2及缩减程度ηp′p″,分别如图2和表4所示.
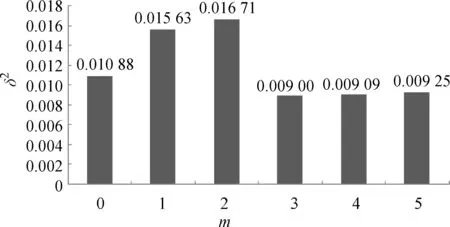
图2 不同m条件下转运中心工作量的方差Fig.2 Flow variances of hubs with different m

表4 ηp′p″的值Table 4 Values of ηp′p″
由图2和表4可知,当增加3个转运中心时,方差才开始减小,且比初始值(m=0即p=4时)还要小,虽然之后方差又开始增大,但其值仍比初始值要小,故使得η78为正,且通过式(7)和(8)计算可知,η47和η48均为正.故若取η=0.01,式(7)~(9)同时被满足.因此,可以认为增加3个转运中心,既能极大限度地减少总运输成本,又能尽可能地均衡每个转运中心的工作量,符合对网络设计的要求.
由上述算例不难发现,适当增加转运中心数量虽能在一定程度上降低工作量的不均衡度及相应的总运输成本,但根据表3可知,无论增加多少个转运中心,对于转运网络而言,转运中心4和17的工作量虽然会有所变化,但仍比其他转运中心的工作量要大得多.尤其是转运中心17,增加转运中心数量后,其工作量几乎没多大变化.这就表明,增加转运中心并重新分配服务节点,一定程度上会让工作量较大的转运中心“减负”,但是由于地理位置等因素所限,这种方法并不是最有效的,因此应考虑扩大转运中心规模,将其建设成大型转运中心,其他的则为小型转运中心,而不是一味地增加数量.
根据以上分析,可以得出以下结论:
(1) 单一分配模式下不考虑容量约束时,转运贴现因子只对总运输成本产生影响,并不会影响最优转运中心选址,这是由单一分配模式的特性所决定.
(2) 在不考虑扩大规模的前提下,要实现转运中心工作量的均衡就必须增加其数量.更多的转运中心意味着更低的总运输成本,但只有增加合适数量的转运中心才会实现工作量的均衡.
(3) 增加转运中心数量一定程度上能均衡每个转运中心的工作量,但由于地理位置等因素的影响,要进一步实现均衡就需要扩大转运中心的规模,将其建设成大型转运中心.
(4) 工作量的方差并不一定会随着转运中心数量的增加而减小,只有在增加合适数量的情况下,工作量的方差才会减小.在网络设计时,应当充分考虑这一特殊关系.
(5) 方差缩减程度满意值η的选取会对转运网络设计产生重要影响,其大小直接关系到转运中心建立的数量,因此选择合适的η值是至关重要的.
3 结 语
本文从单一分配模式下的无容量约束转运网络设计问题入手,考虑到模型的全局最优解可能使得转运中心的实际工作量相差较大,提出以工作量方差缩减程度作为评判准则,通过增加转运中心数量并重新分配服务节点以实现工作量均衡.这能很直观地反映增加不同转运中心数量后的转运网络对于初始转运网络在工作量上改变的趋势,确保了最终得到的最优网络是一种相对较优的情形.当然,该方法也有一定的局限性.由于在单一分配模式下,每个非转运中心只分配给一个转运中心,转运中心的工作量易于确定和分析比较.而在复杂分配模式下,只有在清楚地确定每一条路径的流量大小和所经过的节点后才能衡量各转运中心的工作量,计算较为复杂.因此,在今后的研究中,应当考虑用更有效的方法或模型来评价工作量的均衡性. 另一方面,当转运网络的均衡性不能通过转运中心数量的增加进一步改善时,可以从扩大转运中心规模、调整转运网络的分配模式等方面展开研究.
[1] O’KELLY M E. The location of interacting hub facilities [J]. Transportation Science, 1986, 20: 92-105.
[2] O’KELLY M E. Air freight hubs in the FedEx system: Analysis of fuel use [J]. Journal of Air Transport Management, 2014, 36: 1-12.
[3] KIM H, O’KELLY M E. Reliable p-hub location problems in telecommunication networks [J]. Geographical Analysis, 2009, 41: 283-306.
[4] CAMPBELL J, O’KELLY M E. Twenty-five years of hub location research [J]. Transportation Science, 2012, 46(2): 153-169.
[5] PERRIER N, LANGEVIN A, CAMPBELL J. A survey of models and algorithms for winter road maintenance: Part I system design for spreading and plowing [J]. Computers & Operations Research, 2006, 33(1): 209-238.
[6] PUERTO J, RAMOS A, RODRIGUEZ-CHIA A. A specialized branch & bound & cut for single-allocation ordered median hub location problems [J]. Discrete Applied Mathematics, 2013, 161(16/17): 2624-2646.
[7] ISHFAQ R, SOX C. Hub location-allocation in intermodal logistic networks [J]. European Journal of Operational Research, 2011, 210: 213-230.
[8] MENG Q, WANG X. Intermodal hub-and-spoke network design: Incorporating multiple stakeholders and multi-type containers [J]. Transportation Research Part B: Methodological, 2011, 45(4): 724-742.
[9] ISHFAQ R, SOX C. Design of intermodal logistics networks with hub delays [J]. European Journal of Operational Research, 2012, 220(3): 629-641.
[10] O’KELLY M E. Fuel burn and environmental implications of airline hub networks [J]. Transportation Research Part D: Transport and Environment, 2012, 17(7): 555-567.
[11] FIGUEIREDO R, O’KELLY M E, PIZZOLATO N. A twostage hub location method for air transportation in Brazil [J]. International Transaction in Operational Research, 2014, 21(2): 275-289.
[12] ALUMUR S, YAMAN H, KARA B. Hierarchical multimodal hub location problem with time-definite deliveries [J]. Transportation Research Part E: Logistics and Transportation Review, 2012, 48(6): 1107-1120.
[13] ALUMUR S, KARA B, KARASAN O. Multimodal hub location and hub network design [J]. Omega, 2012, 40(6): 927-939.
[14] ALUMUR S, KARA B, KARASAN O. The design of single allocation incomplete hub networks [J]. Transportation Research Part B: Methodological, 2009, 43(10): 936-951.
[15] CAMPBELL J. Hub location for time definite transportation [J]. Computers & Operations Research, 2009, 36(12): 3107-3116.
Uncapacitated Hub Network Design for Flow Equilibrium
LIShu-xia,FANGChen-hao,WUYi-fan
(Business School, East China University of Science and Technology, Shanghai 200237, China)
The hub flow equilibrium factor is considered in the uncapacitated hub network design problem. First a single allocation hub network model for minimizing total transportation cost is put forward to obtain the initial solution. Then a modified hub network is given by adding hubs so as to balance the amount of flows through different hubs. The optimal number of hubs is obtained based on the given criteria of flow variance reduction degree. Computation experiment with Civil Aeronautic Board data set is also presented. The result shows that the discounting factor of hub does not affect hub location when the capacities of hubs are not limited due to the feature of single allocation mode. In addition, the flow variance reduction criteria can be used for designing single allocation hub network when taking flow equilibrium into account.
hub network design; hub location; flow equilibrium; transportation optimization
1671-0444(2015)04-0485-05
2015-01-14
国家自然科学基金资助项目(71001039, 71101051, 71202053, 71302043, 71431004);中央高校基本科研业务费专项资金资助项目
李淑霞(1975— ),女,河北怀来人,副教授,博士,研究方向为运作系统建模与优化、风险管理.E-mail: sxli@ecust.edu.cn
F 287.3;TB 114.1
A

