立式预制混凝土拱肋施工期温度及收缩裂缝问题研究

凌高祥

立式预制混凝土拱肋施工期温度及收缩裂缝问题研究

凌高祥

（江苏东交工程检测有限公司，江苏 南京 210002）

以某系杆拱桥施工过程中立式预制混凝土拱肋开裂的工程实例为背景，采用理论计算分析，推导了混凝土拱肋温度及收缩应力计算公式，分析了混凝土拱肋在施工期应力变化情况，同时也采用有限元软件建立混凝土拱肋的有限元模型，并将有限元计算结果与理论计算结果进行了对比。研究表明，拱肋受到胎膜的连续约束，在季节性温差及混凝土自身收缩作用下的温度及收缩应力是导致拱肋开裂的主要原因。研究结论对混凝土桥梁预制构件的裂缝防治有一定的意义，同时本文的计算方法可以适用于其他类似结构施工期的开裂分析。

预制混凝土拱肋；温度场；收缩裂缝；有限元分析

混凝土的抗压强度高，而抗拉强度较低，混凝土预制构件生产周期内经常会出现裂缝，这是一个相当普遍的现象，也是长期困扰工程技术人员的技术难题［1］。对于预制混凝土构件施工期裂缝问题，间接作用（温差、收缩等引起的变形受到约束而产生的内力）引起的裂缝占主要部分［2］。

本文主要针对立式预制混凝土拱肋施工期出现裂缝问题，综合考虑拱肋混凝土收缩、季节性温差、底模约束条件，推导出立式预制混凝土拱肋温度及收缩应力计算公式，并将该公式的计算结果与有限元软件模拟的结果进行了对比，总结了底模连续约束时的预制混凝土拱肋早期裂缝成因。

1　工程概况

本文以一座在建的主跨为80 m的下承式预应力混凝土系杆拱桥为背景，该桥为刚性系杆刚性拱柔性吊杆，计算跨径L=78.2 m，拱轴线为二次抛物线，矢跨比为1/5，矢高为15.64 m。拱肋采用工字型截面，拱肋高1.4 m，宽1.2 m。拱肋主要截面如图1所示。

该桥拱肋采用分段预制，上下游共6片拱肋。根据设计图纸的说明，拱肋中间段为拱肋中二段，两边为拱肋中一段，现场的6片按编号分别是拱肋中一段1#（8月4号预制）、拱肋中一段2#（8月4号预制）、拱肋中一段3#（8月17号预制）、拱肋中一段4#（8月17号预制）、拱肋中二段1#（7月19号预制）、拱肋中二段2#（7月25号预制）。

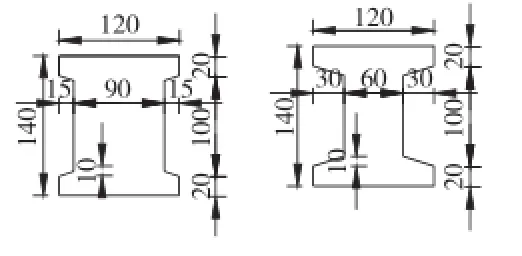
图1　拱肋主要截面图（单位：cm）

2　拱肋裂缝情况

现场人员于2014-10-26发现部分混凝土拱肋开始出现开裂现象，随着环境温度的进一步降低，拱肋裂缝数量进一步增加。针对混凝土拱肋出现开裂的问题，现场人员于2014-10-26和2014-11-28两次对现场拱肋裂缝情况做了检测。现场主要有3片拱肋发生开裂，分别是拱肋中二段1#、拱肋中二段2#、拱肋中一段3#。

以拱肋中二段1#为例，拱肋裂缝情况如下：第一次检测发现该段拱肋出现裂缝9条（朝向东侧5条，朝向西侧4条），最大裂缝长度72 cm，最大裂缝宽度0.3 mm。第二次检测发现该段拱肋又出现裂缝111条（朝向东侧47条，朝向西侧64条），最大裂缝长度30 cm，最大裂缝宽度0.2 mm。如图2所示。

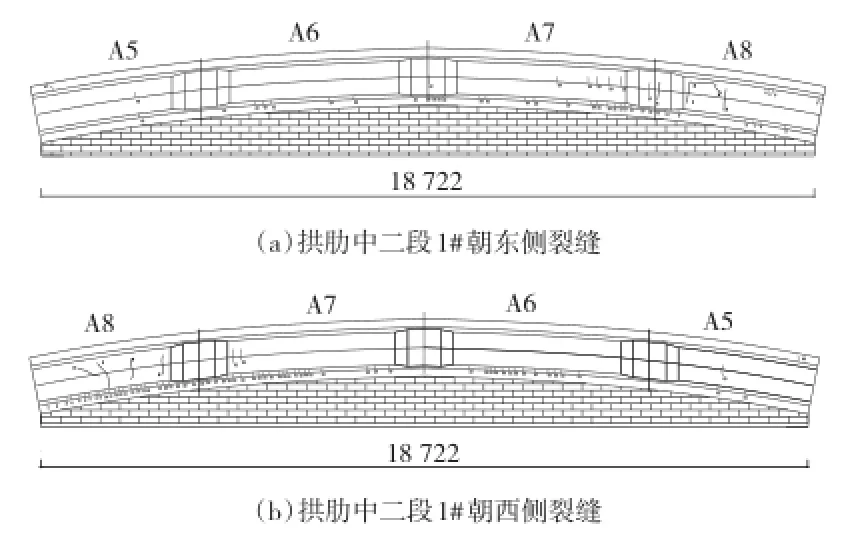
图2　拱肋中二段1#裂缝示意图

3　施工情况调查

3.1拱肋混凝土原材料及配合比

拱肋所用混凝土原材料采用水泥磊达P·Ⅱ52.5，长江Ⅱ区中砂，南京碎石，地下水和减水剂，水泥∶砂∶碎石∶水∶外加剂=435∶683∶1 163∶5.66。

3.2拱肋预制与养护

肋模板采用整体式钢模。混凝土由吊车吊至梁顶下料，混凝土浇筑方向从梁的一端向另一端分层推进，振捣以插入式振动棒振动为主。浇筑时间约4 h。浇筑3 d后拆模。拱肋预制过程包括：胎膜构筑→拱肋钢筋搭设→安装模板（钢模板）→模板加固→灌注混凝土→拆除模板。

该桥拱肋拆模时间为拱肋浇筑完成后第3天，由于大气温度较高，现场采用湿养护，拱肋采用湿布覆盖，拱肋采用洒水养护，白天连续洒水养护。拱肋浇筑期间，白天温度在35 ℃ 左右，夜间温度在26 ℃左右，平均相对湿度72%，风速较小。湿养护时间持续7 d。薛窑桥混凝土拱肋2014年七八月份即完成浇筑工作，但是拱肋直到2014-12才开始吊装，期间间隔将近半年时间。

4　拱肋裂缝原因初步分析

该桥混凝土拱肋在完成浇筑拆模后，并未发现裂缝，而是在将近3个月之后发现裂缝。从裂缝出现的时间上判断，基本可以排除由于拱肋早期水化热过大，导致构件自约束应力超过构件允许应力而产生裂缝。根据检测结果现场混凝土水灰比、水泥用量、水泥品种、粗骨料、外加剂的使用基本满足施工规范的要求，而拱肋拆模时间、后期养护也基本满足要求。现场人员初步判断，拱肋裂缝的产生是由于拱肋的温度及收缩变形受到胎膜的约束，在构件内部产生了温度及收缩应力（外约束应力），当该应力超过了混凝土自身抗拉强度时，便会引起拱肋开裂。随着环境温度的进一步降低，裂缝会继续发展。

5　拱肋温度及收缩应力理论计算

5.1公式推导

在拱肋的任意点S处，截取一段ds长的微体，由于均匀受力假定，微体的高度取全高h，其厚度为t，承受均匀内力为N（即σs的合力），剪力Q，地基对拱肋的法向力为FN和剪力为 FT（即τ的合力）。如图3所示。

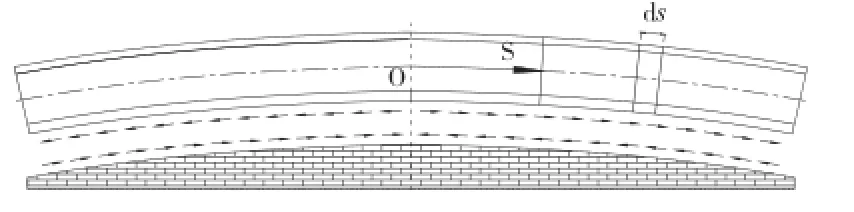
图3　拱肋受力简图

取拱肋的一个微单元，进行受力分析，微单元如图4所示。

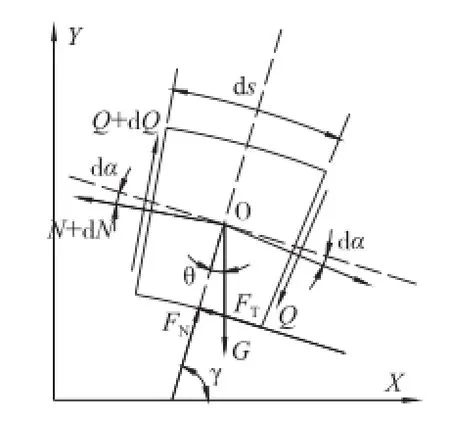
图4　拱肋微单元

列出平衡方程如下：

将上述表达式化简可得：

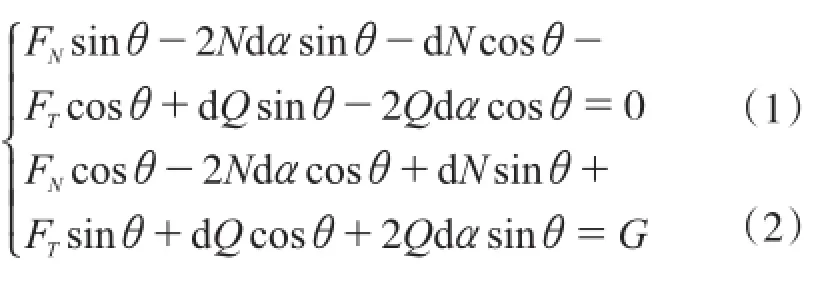
将式（1）乘以cosθ，式（2）乘以sinθ，两式相减可得：

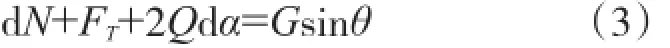
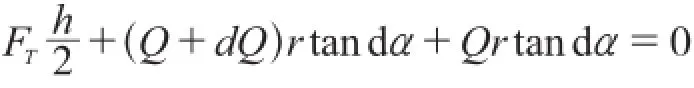
略去高次项，上述表达式化简可得：

将式（4）带入式（3）表达式中，可得：

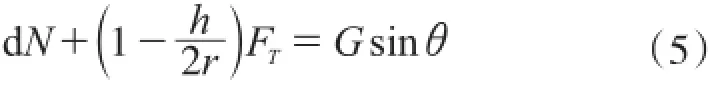
其中，FT=τtds，dN=Adσs，G=ρAds，（A是拱肋截面面积，ρ是拱肋密度），则式（5）可以化为：

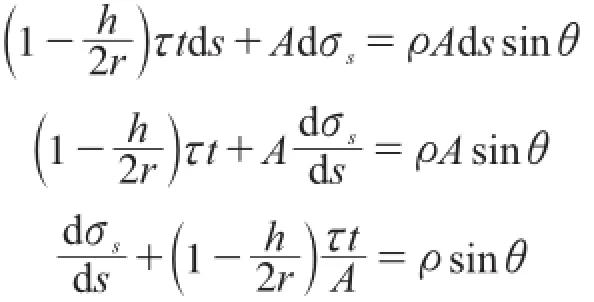
任意点的位移由约束位移与自由位移合成［1］：

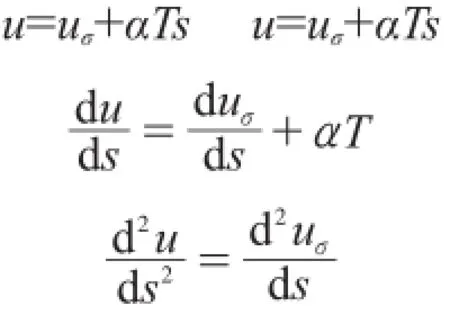
式中：u为任意点位移，uσ为约束位移，αTs为自由位移，由弹性力学物理和几何关系可得：

将式（6）两边对s求导可得：

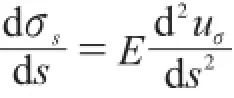
Cx为基础的水平阻力系数［1］，其与接触点水平位移有关，本文基于弧坐标推导，为了简化计算过程，对其进行坐标变化，假定引入参数底板沿弧长的阻力系数Cs：

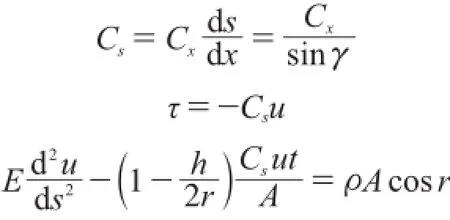
令：

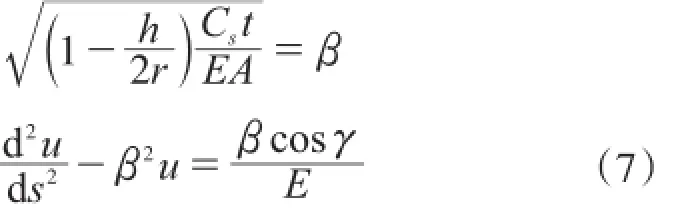
式（7）为二阶非齐次线性方程，其解由对应的齐次方程的通解与非齐次方程的特解组成，对应的齐次方程通解为：

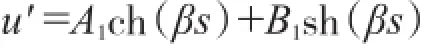
而非齐次线性方程特解为：

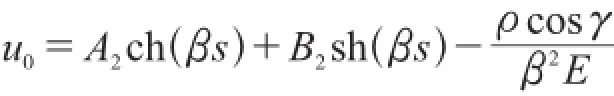
式（7）的通解为：

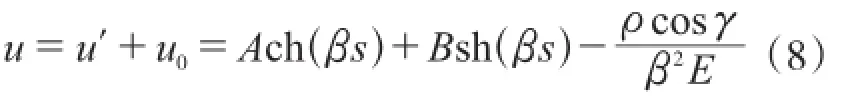
该方程的边界条件为：

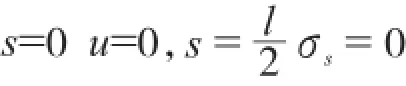
将s=0 u=0带入式（8）可以解得：

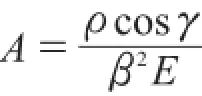
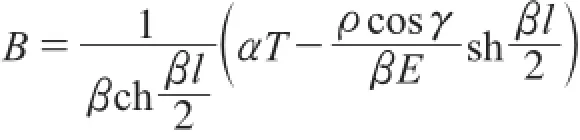
此时可以得到二阶非齐次线性方程式（7）的通解，拱肋截面任意一点位移：

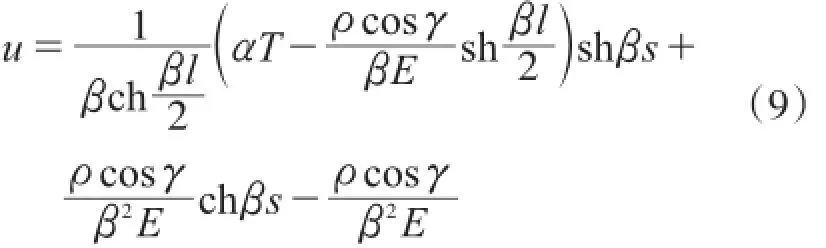
可得任意一点的应力σs的表达式：

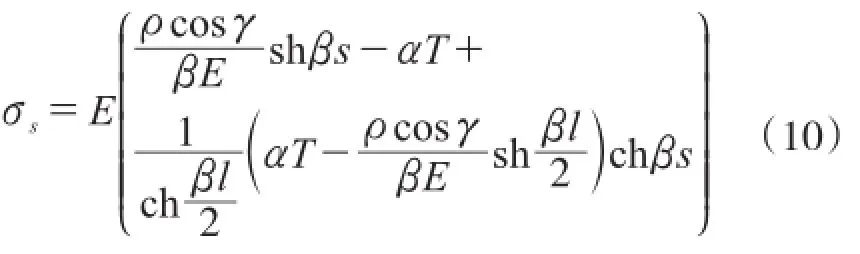
当s=0，此时可得：σs=σsmax

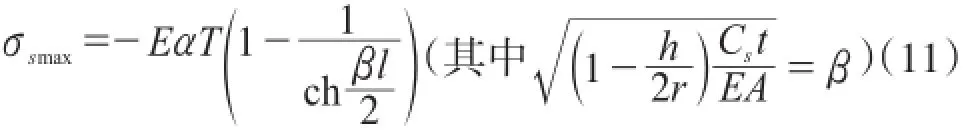
若考虑混凝土应力松弛时最大应力为：

为了较为确切地计算早期混凝土的温度应力，考虑弹性模量以及松弛系数随时间的变化，将温差分为许多区段ΔT，各段内将E（t）及H（t，τ）看作常量，所以可得：

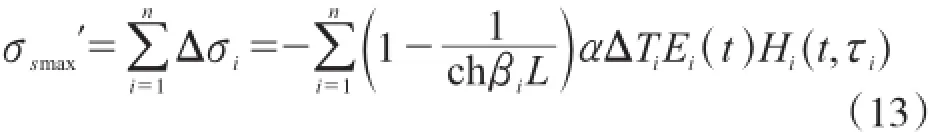
式中：ΔTi表示将温差分解为n段，ΔTi为第i段温差；Ei（t）为第i段降温时的弹性模量；Hi（t，τi）为第i段龄期τi的应力松弛系数。

5.2工程计算

5.2.1 温差T的计算

混凝土拱肋温差主要包括两个方面：自由收缩转化的当量温差T1和季节性温差T2。

（1）自由收缩转化的当量温差计算

本文利用CEB-FIP90［3］、AASHTO［4］、ACI-209（92）［5］及王铁梦［1］收缩模型，可以求得混凝土拱肋自由收缩应变值，计算结果如图4所示：

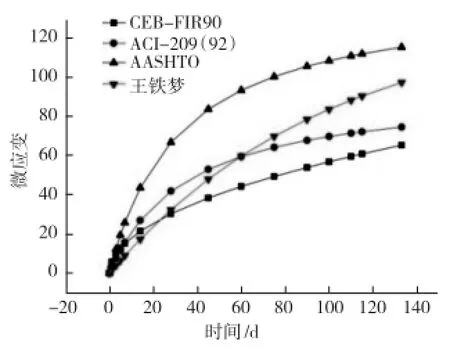
图4　几种预测模式拱肋收缩应变值曲线

收缩当量温差取AASHTO的计算结果（不利工况）。

（2）季节性温差

季节温差是指初始温度T0与最低温度Tmin的差值DT［6］（为了方便表述，下面用T2代替DT）。当地环境最高和最低温度随时间变化曲线如图5所示。

（3）初始温度T0

新浇混凝土具有先膨胀后收缩的变形特征；与混凝土侧压力为零的时刻相对应，可将其膨胀变形结束、收缩变形开始的时间定义为混凝土的凝结时间［7］。本文选取拱肋浇筑1 d后，拱肋的温度作为结构的初始温度。本文通过有限元软件模拟拱肋浇筑期间的水化热变化情况，可以得到拱肋浇筑1 d后，拱肋的温度分布情况，如图6所示。

根据有限元计算结果，综合选取拱肋的浇筑后中心温度为43.651 ℃。

（4）分阶段考虑降温作用

为了较精确地计算考虑徐变作用下的温度应力，将总降温分成若干台阶式降温，分别计算出各阶段降温引起的应力，最后叠加得出总的降温应力。由收缩转化的当量温差T1、季节性温差T2、初始温度T0，可以得到台阶式降温ΔTi，结果如表2所示。

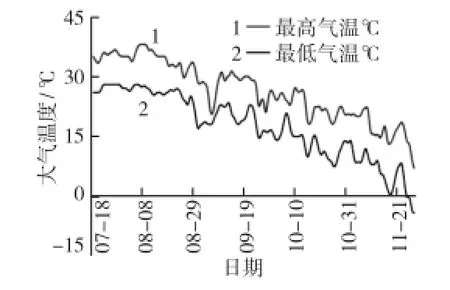
图5　当地环境最高和最低温度随时间变化曲线

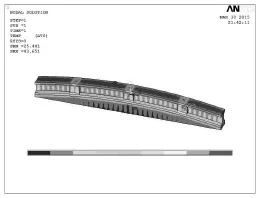
图6　拱肋浇筑1 d后温度分布情况

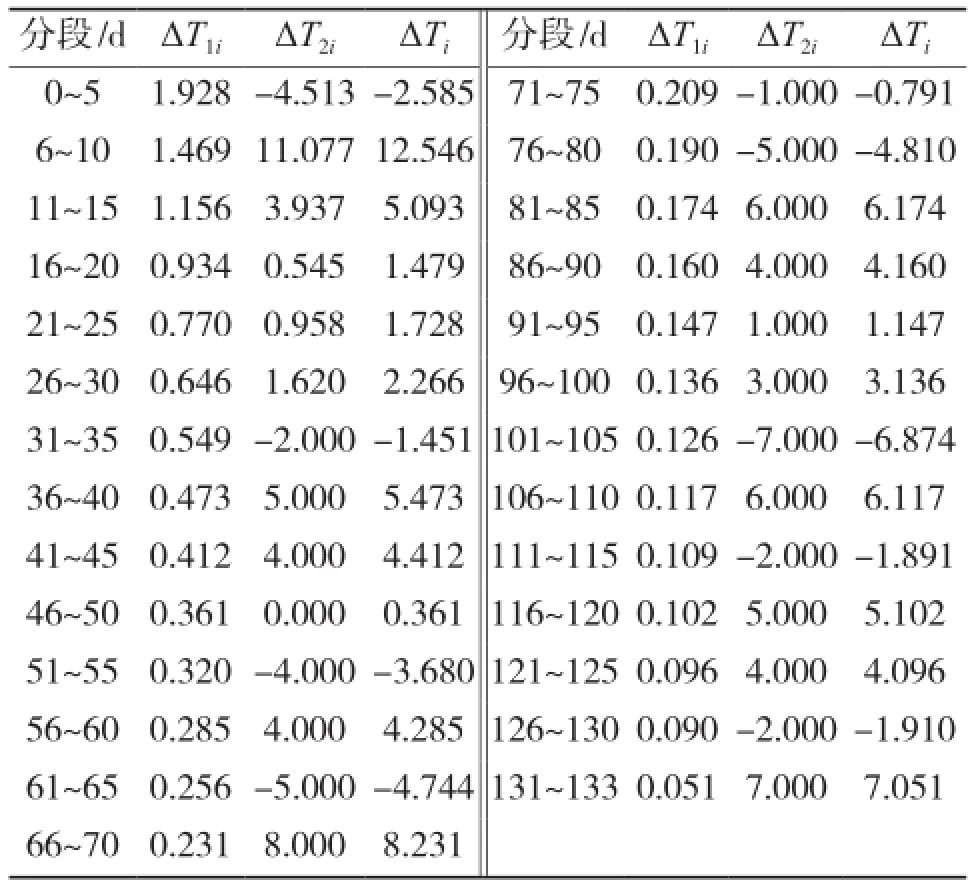
表2　各个阶段温差计算表

5.2.2 混凝土弹性模量及松弛系数

本文考虑混凝土弹性模量随混凝土龄期的变化，采用如下计算公式［1］：

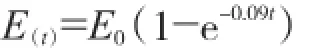
而松弛系数随龄期的变化，参考文献［1］给出的应力松弛计算表格。

5.2.3 拱肋温度及收缩最大应力值计算

带入上述温度，弹性模量，松弛系数基本参数，以及拱肋基本特征参数：t=1.2×103mm，A=1.14×106mm2，l=2.340 9×106mm，Cx=0.35 N/mm3，计算结果如图7所示。

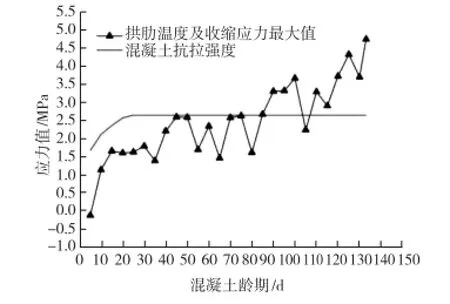
图7　拱肋温度及收缩应力最大值随龄期变化曲线

理论计算的结果显示，混凝土温度及收缩应力最大值随着混凝土龄期的增大也逐渐增大，现场在2015-10-26检测出拱肋裂缝，对应的混凝土龄期是100 d。从图7可以看出，此时混凝土拱肋温度及收缩应力为3.666 MPa，超过了混凝土的抗拉强度。随着环境温度进一步降低，温度及收缩应力也进一步增大，2015-11-28温度及收缩应力达到4.745 MPa，而现场检测拱肋裂缝也逐渐增多，理论计算和现场裂缝的变化情况较为吻合。

6　有限元模拟计算

6.1基本单元和工况

本文采用Ansys进行有限元模拟计算，拱肋和胎膜采用实体单元模拟，热分析时为实体单元solid70，结构分析时转化为实体单元solid45。

拱肋和胎膜接触部位，采用接触单元模拟，用Targe170和Conta174面面接触单元来描述相互作用，拱肋下表面为接触面conta174，胎膜上表面为目标targe170。采用该接触单元模拟可以达到3个效果：（1）传递切向摩擦力；（2）传递法向压力；（3）不传递法向拉力，不互相渗透。计算拱肋应力场时，胎膜的底部为固定支撑。

混凝土拱肋所受的荷载主要是混凝土自重以及温差作用、混凝土收缩变形所产生的作用。收缩变形作用如前第5节所述转换为当量温差。

荷载工况选取按照5.2.1中各个阶段温差划分，共有27个工况。

6.2温度场模拟结果

有限元模拟结果如图8所示，从图中可以看出有限元结果和理论结果有相同的变化趋势，但是有限元结果偏大，以第100天为例，理论计算结果为3.666 MPa，而有限元的计算结果为4.131 MPa。这是由于建模过程中考虑了拱肋的截面变化，理论计算时未考虑截面的变化。

从有限元计算结果中可以看出，拱肋下翼缘比拱肋上翼缘更容易开裂，以工况27为例，拱肋下翼缘应力增量1.88 MPa大于拱肋上翼缘的应力增量1.39 MPa。

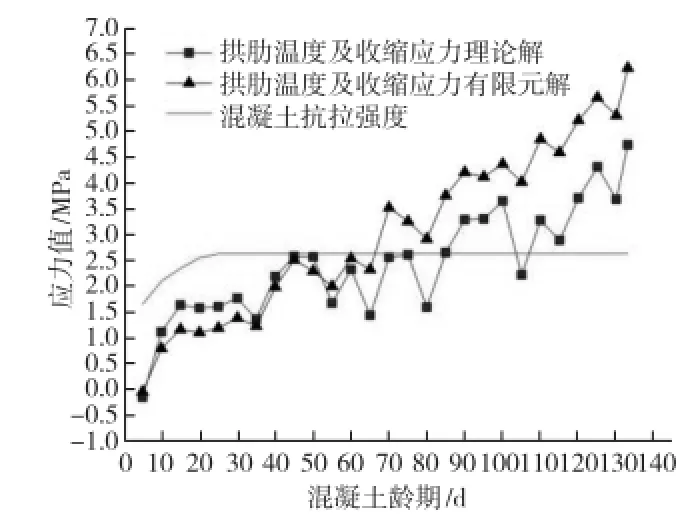
图8　拱肋温度及收缩应力最大值理论解和有限元解比较

7　结语

本文主要针对立式预制混凝土拱肋施工期出现裂缝问题，结合现场拱肋裂缝检测情况，综合考虑拱肋混凝土收缩、季节性温差、底模约束条件，推导出立式预制混凝土拱肋温度及收缩应力计算公式，并将该公式的计算结果与有限元软件模拟的结果进行了对比。

本文认为该立式预制混凝土拱肋裂缝产生主要原因是：随着环境温度的下降，混凝土拱肋发生温度变形，以及混凝土自身的收缩变形，这两种变形都受到了胎膜的约束，致使构件内部产生了温度及收缩应力（外约束应力），当该应力超过了混凝土自身抗拉强度时，便会引起拱肋开裂。

［1］王铁梦.工程结构裂缝控制［M］.北京：中国建筑工业出版社，1997.

［2］袁勇.混凝土结构早期裂缝控制［M］.北京：科学出版社，2004.

［3］CEB-FIP. CEB-FIP Model Code for Concrete Structures［S］. 1990.

［4］AASHTO. AASHTO LRFD Bridge specifications SI Units Third Edition［S］. 2004.

［5］ACI 209R—92.Prediction of creep，shrinkage and temperature effects in concrete structures［S］. 1992.

［6］王庆龙.超长混凝土结构温度及收缩裂缝控制方法研究［D］.南京：东南大学，2005.

［7］ 侯东伟，张君，孙伟.基于早期变形特征的混凝土凝时间的确定［J］.硅酸盐学报，2009（7）：1079-1084.

Study on Temperature and Shrinkage Crack Problem of Precast Concrete Arch during Construction Period

Ling Gaoxiang
（Jiangsu Easttrans Engineering Detection Co.Ltd， Nanjing 210002， China）

Based on vertical precast concrete arch rib cracking during arch construction process， by theoretical calculation and analysis， this paper derived stress calculation formulas of temperature and shrinkage for concrete arch rib， and analyzed stress changes for concrete arch rib during the construction period. It also established the finite element model of concrete rib by using the finite element software， and finite element results with theoretical results were compared. The results showed that continuous rib bound by membranes， the temperature and shrinkage stress in seasonal temperature differences and its own contraction was the major causes of arch rib cracking. The conclusions had some significance for crack prevention precast of concrete bridge， and the calculation method in this paper could be applied to the analysis of other similar structures cracking during the construction period.

precast concrete arch； temperature field； constraction crack； FEA

U448.22+5

A

1672-9889（2015）06-0044-05

凌高祥（1983-），男，江苏阜宁人，工程师，主要从事道路和桥梁研究工作。

（2015-11-09）