DELTA机器人传送带与视觉的综合标定方法*
杨 强,刘冠峰
(广东工业大学机电工程学院,广东广州510006)
DELTA机器人传送带与视觉的综合标定方法*
杨强,刘冠峰
(广东工业大学机电工程学院,广东广州510006)
提出一种关于DELTA机器人传送带与视觉的综合标定方法。通过DELTA机器人臂末端在传送带移动一段距离接触传送带始末同一点,得到该点在机器人坐标系的位置和编码器上对应的读数,得到传送带与机器人的比例因子,确定机器人坐标系与传送带坐标系的转化矩阵,从而得到传动带相对于机器人坐标系的位姿,即传送带的标定。通过相机定位与机器人接触同一点,从而确定相机的内参矩阵与外参矩阵,从而得到机器人与相机坐标系的转换关系,即机器人视觉的标定。DELTA机器人传送带与视觉的标定,为DELTA机器人高精度控制的实现打下基础。
DELTA机器人;传送带;相机;标定
DOI:10.3969/j.issn.1009-9492.2015.01.002
0 引言
DELTA机器人具有刚度强、精度高、自重负荷比小、速度高等显著优点,能完成各种形状类型的小产品的拾取和放置动作[1]。如图1所示,由于机器人坐标系、相机坐标系与传送带坐标系均为独立坐标系,因此需要对传送带标定[2-3],对视觉标定[4],使三者互相联系形成闭环链的转换关系,从而可以控制DELTA机器人臂末端能够准确抓取移动传送带上的物体。所谓标定,就是应用先进的测量手段和基于机器人的结构参数辨识出机器人模型的准确转换关系[6-8],从而提高机器人绝对精度的过程。但是由于DELTA机器人的理想结构参数与实际的结构参数相比通常存在偏差,并且在安装过程中不能保证传送带移动方向平行于机器人坐标系X轴方向,传送带平面垂直于机器人坐标系Z轴方向,它们之间存在微小角度偏差,从而影响机器人的精度。直接提高机械加工与安装精度将极大地增加制造成本,而通过本文提出的方法对机器人进行标定可以避免机器人安装误差,并且能够获取机器人准确的结构参数来提高机器人精度。这种标定方式对DELTA机器人控制具有很高的实用价值。

图1 DELTA机器人
1 传送带标定
1.1转换矩阵和比例因子
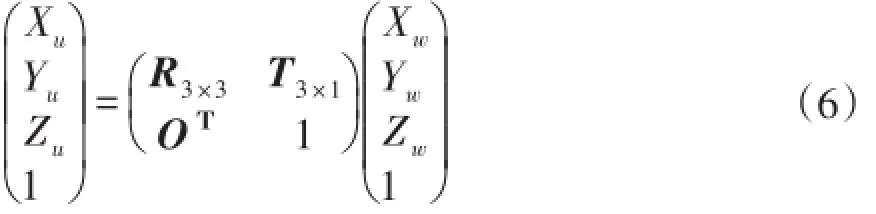
传动带的标定就是确定传动带相对于机器人坐标系的位姿[5]。设机器人坐标系为R,传送带坐标系为C,那么传动带坐标系相对于机器人坐标系的变化矩阵为。如果知道这个变化矩阵和物体在传送带坐标系下面的姿态PC,那么就能知道该物体在机器人坐标系下的姿态。即:

1.2传送带的标定方法
(1)在传送带上确定一点为P,移动DELTA机器人,将其臂末端触碰到该点P,记录传送带的编码器值的位置读数为Ve1,而此时DELTA机器臂末端的位置为
(2)在保证DELTA机器人可以再次触碰到P的条件下,移动传送带并且让这段移动的距离越大越好。再次移动机器人,使其臂末端触碰到P点。记录编码器的位置读数值为Ve2,DELTA机器人末端的位置为
(3)让机器人沿着传送带垂直的方向移动一段距离,记录机器人臂末端触碰到传送带时候的位置
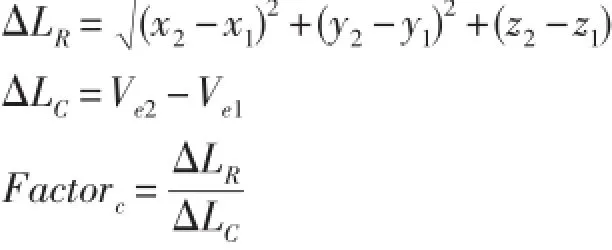
当测量出传送带移动一段距离两个位置编码器的读数Ve与Ve',即可确定机器人移动的距离ΔL。
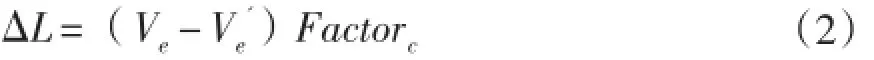
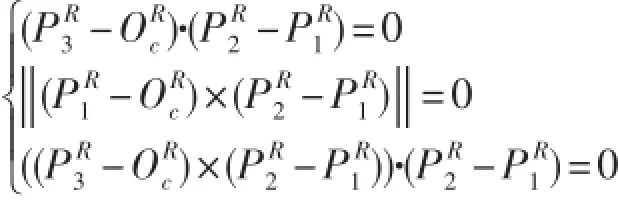
通过上式可以求得:

其中:

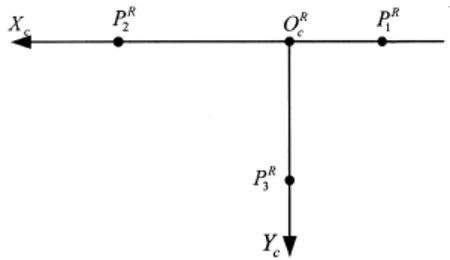
图2 传送带坐标
得到传送带基坐标系的表达式:
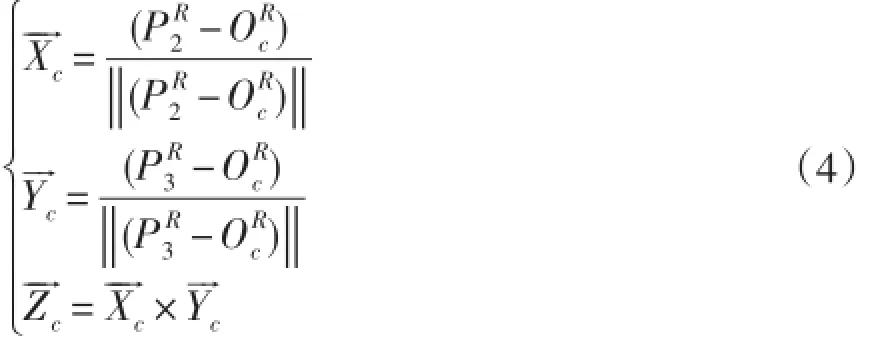
通过式(2)和(4)可以求得传送带坐标系与机器人坐标系的转换矩阵

传送带移动的方向为传送带坐标系的Xc轴方向,相机测量在传送带坐标下初始点为PC,及测量传送带移动一段距离两个位置编码器的读数,则由式(1)、式(2)和式(5)可以确定终点在机器人坐标系下的位置PR。
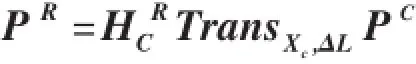
其中:
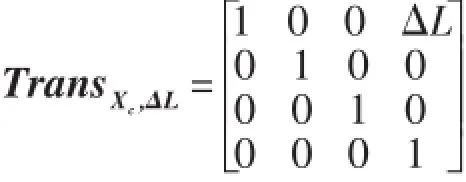
通过这种传送带的标定方法,可以确定传送带传在送过程中各坐标在机器人坐标系中的准确位置,从而使机器人臂末端能准确抓取传送带上的物体。由于传送带坐标系OcXcYcZc建立在传送带移动过程中,因此建立的传送带坐标系的Xc方向平行于传送带移动方向,Yc方向垂直于传送带移动方向,Zc方向垂直于传送带平面。这样的标定方法可以避免安装传送带与机器人过程中引入的角度偏差,即不用考虑传送带移动方向平行于机器人坐标系X轴方向,传送带平面垂直于机器人坐标系Z轴方向,以及它们之间存在的微小角度偏差。
2 视觉标定
2.1视觉标定原理
摄像机在计算机视觉中是对物理三维世界进行重建的一种基本工具,通过这个重建过程,可以计算处理得到的二维图像,来描述、识别、处理外部三维世界。对摄像机的标定[9],是通过二维图像认识外部三维世界的第一步。摄像机的标定就是建立三维空间坐标和二维图像坐标的对应关系。
标定过程中,涉及到几个坐标系:世界坐标系、相机坐标系、图像像素坐标系和图像物理坐标系。世界坐标系是由用户定义的三位坐标系,用来描述三维空间的物体、相机的坐标位置,在这里世界坐标系是机器人坐标系;相机坐标系是以相机光心作为原点,Z轴与光轴重合,满足右手法则;图像像素坐标是以图像左上角为原点,以像素为坐标单位的直角坐标系;图像物理坐标系是以光轴与像平面的交点为原点,以毫米为单位的直角坐标系。
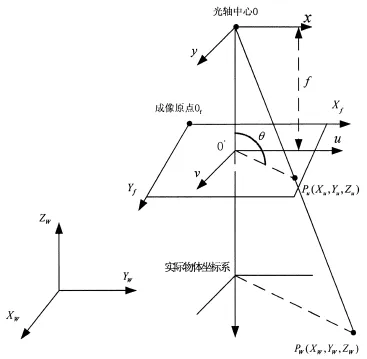
图3 理想透镜的摄像机成像模型
对于从相机坐标系到像平面坐标系的变换,像平面坐标系是用像素单位来表示的,而相机坐标系则是以毫米为单位来表示,因此,要完成改变换过程就需要先得到像平面的像素单位与毫米单位之间的线性关系。在图(3)中,相机光轴中心Z轴方向上与像平面的交点O'称为投影中心,坐标为(cx,cy),是像素单位,而每个像素在Xf和Yf的物理尺寸为单位是像素/毫米,则像平面的像素与毫米间的线性关系如下:
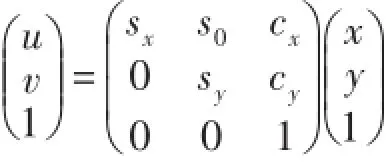
由小孔模型下投影变换原理,可知:
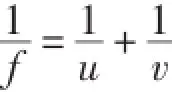
其中,f为焦距,u为物距,v为相距。因此像平面的物理坐标(x,y)对应的相机坐标系满足公式:
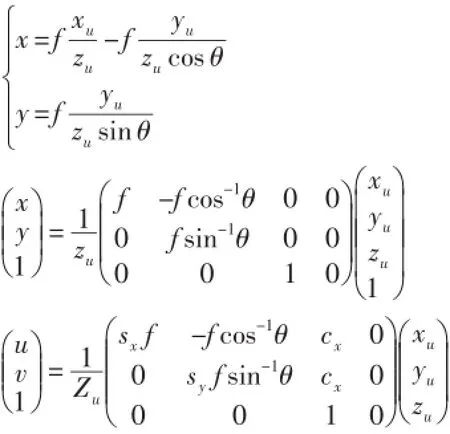
其中,平移矩阵T是三维列向量,旋转矩阵R是坐标轴依次绕x,y和z轴旋转角度ψ,φ和τ所形成的三个矩阵Rx(ψ),Rx(φ),Rx(τ)的总乘积。它们的定义如式:
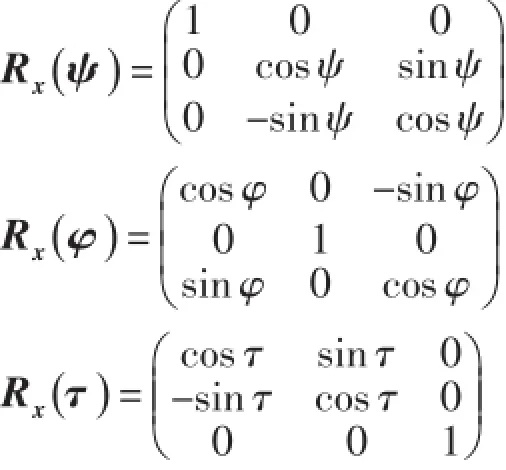
则矩阵R的计算公式如式:
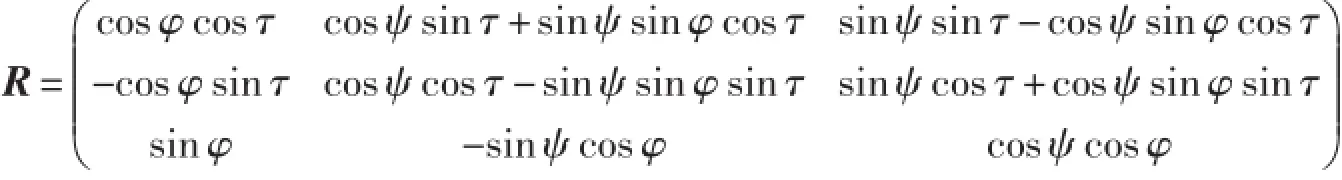
相机的标定其实就是确定内参数矩阵和外参数矩阵。
2.2基于机器人的相机标定
基于机器人的标定主要是指依靠机器人坐标系来标定相机,确定二者之间的转化矩阵,一般情况下,相机被安装在工作空间之内。
基于机器人的标定步骤如下。
(1)确定相机的内参:图5是标准的标定块,色块的尺寸和色块间隔为已知的,该步骤之后,可以确定相机的内参数。设传送带一点Pi经过相机内参数矩阵转换处理后,读得在相机物理坐标系下的位置为
(2)用相机分别定位图6中四个目标点的位置(像素坐标)。手动移动机器人,让机器人能触碰到这四个目标点P1、P2、P3及P4,分别测量出它们在机器人坐标系的位置,由上节传送带标定得到HRC,即可求出四个目标点在传送带坐标系下的位置(世界坐标),由式(6)可确定相机的外参矩阵,相机坐标系与传送带坐标系的转换关系如下:
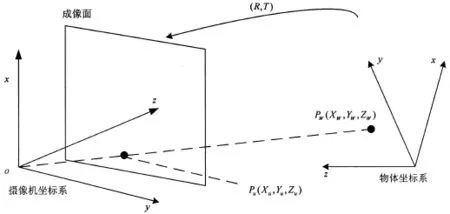
图4 机坐标系到世界坐标系的变换
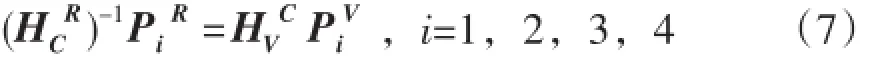

图5 视觉标准的标定块
由式(7)得到相机坐标系与传送带坐标系的转换矩阵:

2.3基于传动带的视觉标定
基于传送带的标定,是指相机安装在机器人工作空间外的情况下,依靠传送带坐标系,确定传动带坐标系与视觉坐标系的关系。通过传动带坐标系这个媒介来确定视觉坐标系与机器人坐标系之间的转换矩阵,最终确定相机的外参,即世界坐标系与相机坐标系之间的关系。
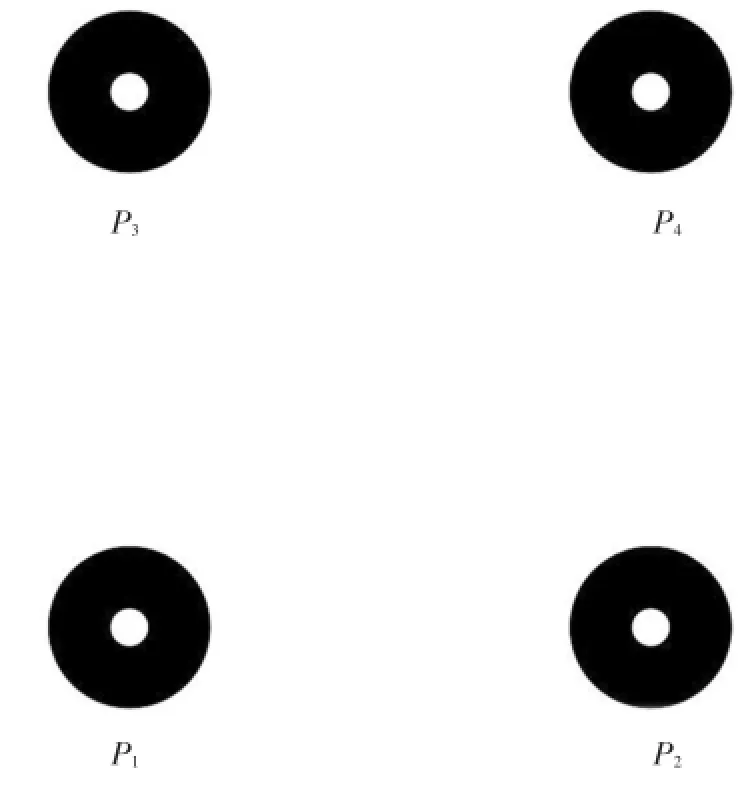
图6 目标点
基于传送带的标定步骤如下。
(1)与“基于机器人的相机标定”步骤一相同,确定相机内参,读得在相机坐标系下的位置为PVi。
(2)由于相机在机器人工作空间之外,所以在标定相机外参数的时候,需要借助传送带编码器。相机定位之后,移动传送带一段距离ΔL',让标定目标移动到机器人的工作空间之内。让机器人分别去触碰这四个点。由上文传送带的标定已经得到机器人与传送带的比例因子Factorc以及两坐标系的转换关系。所以P1、P2、P3及 P4转化到传送带坐标系中分别对应为。经过上述步骤可以得到相机坐标系与传送带坐标系的转换关系如下:
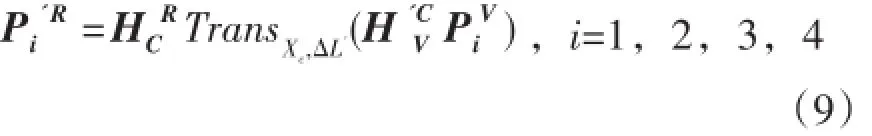
由式(9)得到相机坐标系与传送带坐标系的转换矩阵:
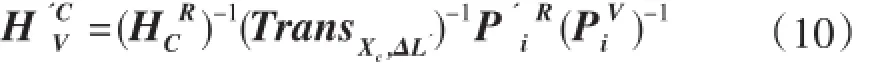
3 实验与数据
传统标定方法是假定传送带极坐标系与机器人坐标系仅原点坐标有位置偏移关系,而本文建立的传送带坐标系则考虑了安装过程中角度的偏差。在机器人坐标系下测量五组数据,对本文的标定方法与传统标定方法进行误差比较。
假设初始点为A0,在机器人坐标系下测量得到的位置为(-432.197,28.387,-730.534),传送带每次移动180 mm,分别为测量出A0五次移动后在机器人坐标系下的位置为:A1(-251.945,31.485,-729.135),A2(-72.245,33.523,-726.473),A3(106.202,35.123,-723.0491),A4(287.521,38.123,-720.921),A5(466.901,41.562,-718.767)。
通过两种标定方法分别得到在上述传送带移动五次后的位置数据,由表1,可以看到本文标定方法的最大偏差3.448 mm。而传统标定方法最大偏差14.504 mm。
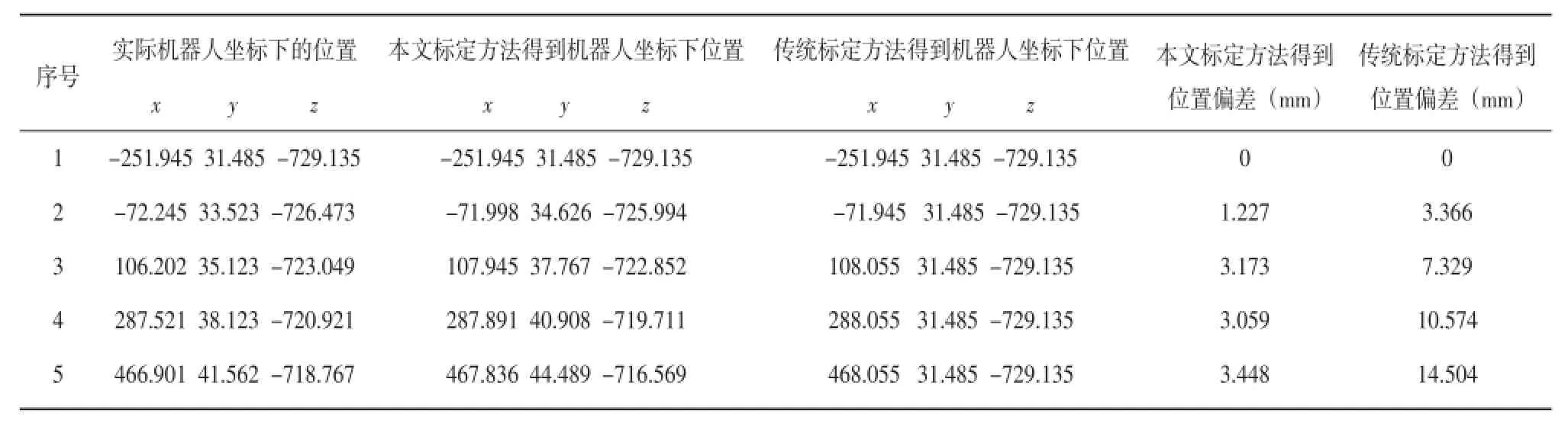
表1 R两种标定方法得到数据及偏差
4 结论
本文提出了一种在传送带移动过程中进行DELTA机器人、传送带与视觉的综合标定方法。同时建立的机器人坐标系、传送带坐标系与相机坐标系。通过这种标定可以确定机器人坐标系、传送带坐标系与视觉坐标系之间的转换关系。
该标定方法与传统标定方法相比,考虑了安装过程中传送带坐标系与机器人坐标系的角度偏差,更符合实际中DELTA机器人的运用。通过试验得到的结果表明该标定方法具有较高的精度,并且成功地提高了机器人运动控制的精准性,满足一般的工程需求,具有很高的实用性。
[1]李毅.高速并联机械手运动学标定方法研究[D].天津:天津大学,2009.
[2]彭斌彬,高峰.并联机器人的标定建模[J].机械工程学报,2003,41(8):132-135.
[3]唐国宝,黄田.Delta并联机构标定方法研究[J].机械工程学报,2003,39(8):55-60.
[4]李振,张玉茹,刘军传.一种基于机器视觉的机器人标定方法[J].机械设计与研究,2007,23(3):66-69.
[5]Jorge A.Fundamentals of robotic mechanical systems,Theory,Methods and Algorithms[M].SPringer-Ver⁃lagNYUSA,1997.
[6]Renaud P,Andreff N,Marquet F,et al.Vision-based kinematic calibration of a H4 parallel mechanism[C]. //2003 International Conference on Robotics and Automa⁃tion:Vol.1.Piscataway,NJ,USA:IEEE,2003: 1191-1196.
[7]Renaud P,Andreff N,Lavest J M,et al.Simplifying the Kinematic Calibration of Parallel Mechanisms Using Vision-Based Metrology[J].IEEE Transaction on Ro⁃botics,2006,22(1):12-22.
[8]王栋,曹彤,宋虎,等.联合实验和仿真的机器人参数标定[J].机电工程,2013(10):1182-1187.
[9]解则晓,辛少辉,李绪勇,等.基于单目视觉的机器人标定方法[J].机械工程学报,2011,47(5):35-39.
[10]袁国栋,秦开怀,胡伟.基于单幅透视图像确定相机参数的几何方法[J].计算机研究与发展,2006,43(11):1933-1938.
(编辑:阮毅)
Method of Integrated Calibration on DELTA Robot Conveyor and Vision
YANG Qiang,LIU Guan-feng
(School of Electro-mechanical Engineering,Guangdong University of Technology,Guangzhou510006,China)
In this paper we propose an method of integrated calibration on DELTA robot conveyor and vision.We first use the end of DELTA robot arm to touch the same point on the conveyor when the conveyor moves some distance,which allows us to obtain the value of the point's location in the robot coordinate system and the corresponding value of the encoder.,then we get the scale factor of the robot and conveyor,determine the transformation matrix between the robot coordinate system and the conveyor coordinate system,then we can know the pose of the conveyor coordinate system relative to the coordinate system of the robot,which is the conveyor calibration.By using the camera to posit in contact with the robot at the same point,we obtain the intrinsic matrix and the external parameters matrix of the camera,which can know the transformation matrix between the robot coordinate system and the camera coordinate system,which is the robot vision calibration.DELTA robot conveyor and vision calibration will make the foundation of achieving DELTA robot high-precision control.
DELTA Robot;conveyor;camera;calibration
TP242.6+2
A
1009-9492(2015)01-0005-06
*广东省高等学校人才引进专项资金(编号:2050205);国家自然科学基金,青年科学基金项目(编号:50505009);国家自然科学基金项目(编号:51375095)
2014-09-12
杨强,男,1989年生,广东韶关人,硕士研究生。研究领域:工业机器人轨迹规划。

