Buck变换器在输出电压宽范围可调应用领域若干关键技术
陈家新,彭小龙,华 华,林 毅
(东华大学 机械工程学院,上海 201620)
Buck变换器在输出电压宽范围可调应用领域若干关键技术
陈家新,彭小龙,华华,林毅
(东华大学 机械工程学院,上海 201620)
在研究了Buck变换器的纹波变化特征基础上,给出了连续状态下电路主要参数的代数表达式及控制系统的设计技术.通过系统仿真,指出了分岔特性给变换器输出纹波以及控制时间延迟给低输出电压的稳定控制所带来的不利影响.
Buck变换器; 纹波;连续状态(CCM);稳定性;分岔特性
以往大多采用线性调整的稳压方式[1]实现输出电压宽范围调节,其存在功率密度低、效率低等缺点.与传统线性直流电源相比,开关电源具有输入电源工作电压宽、转换效率高、体积小、质量轻等优点.然而,开关电源应用于固定电压的输出中,其电压可调范围有限,尤其是开关电源在通用电源的宽范围可调应用上还并不普遍.产生这一现象的原因有很多,其中电源参数设计、开关电源的纹波、最小稳定输出电压和宽范围系统稳定性,是进一步改进宽范围工作开关变换器性能要解决的主要问题.
文献[2]给出了固定负载下利用PWM(pulse width modulation)控制电压宽范围输出DC-DC(direct current-direct current)变换器的控制策略.文献[3]设计了一种宽范围连续可调的DC-DC变换器,考虑了负载的变化对系统的影响.文献[4]研究了Buck-Boost电路,给出了一种系统稳定性的分析方法,为宽范围输出开关电源的稳定性分析提供了新思路.
然而负载大范围变化时系统震荡会加大,输出电压变化时纹波也会发生变化.这些因素的考虑对宽范围开关电源提出了新的要求.结合上述文献研究,本文给出Buck变换器在全负载范围变化下系统都能稳定,以及在全范围输出的情况下纹波都能满足系统要求的设计方法.由于Buck变换器的非线性特性,会发生分岔现象,而由于PWM芯片的局限性,使得输出无法达到零电压,这些都需要通过仿真进行进一步的揭示.
Buck变换器电路图如图1所示.假定所有元器件皆为理想元件,Buck变换器具体特性参数如表1所示.
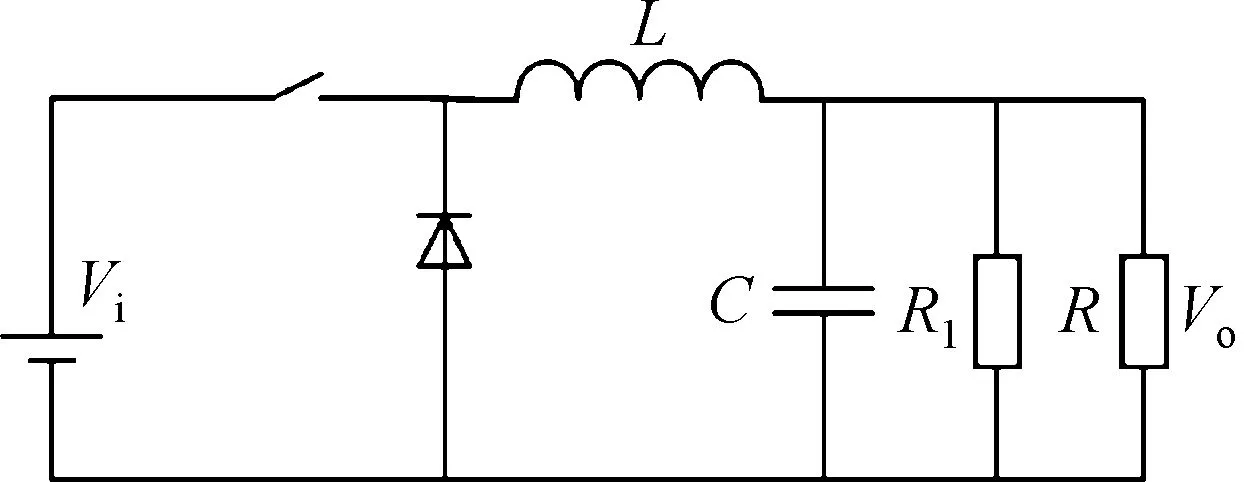
图1 Buck电路图Fig.1 Buck circuit diagram

表1 Buck变换器的参数Table 1 Buck converter parameters
1 Buck变换器主要参数确定
本文设计的Buck变换器工作在CCM(continuous conducting mode)模式下,从而建立大信号状态平均模型[5].
1.1纹波电流计算
当系统在CCM下,占空比D为
(1)
当功率开关管导通时
(2)
其中:L为电感量;T为PWM周期.
由式(1)和(2)得纹波电流Irp为
(3)
当D=0.5时,纹波电流最大.
1.2纹波电压计算
输出电容的电流ic等于电感电流iL减去输出电流Io.而在CCM模式下输出电流近似等于电感电流上升段或下降段中心值,因而电感电流上升段电容存在两个状态,即先放电后充电,且时间相等.同样在下降段,电容先充电后放电,且时间也相等.所以整个电容充放电时间相等.图2为电压和电流波形.
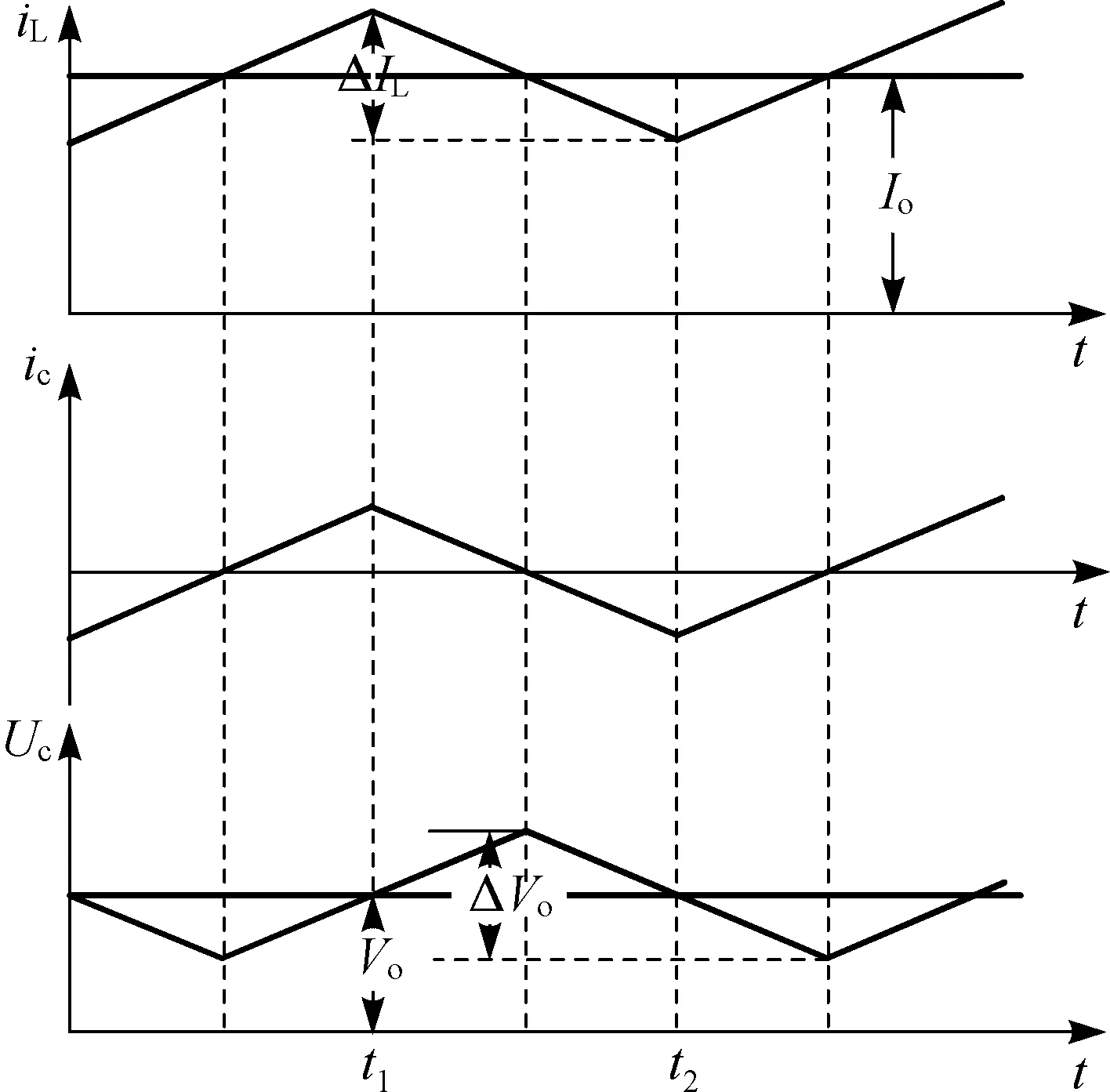
图2 电压和电流波形Fig.2 Voltage and current wave
当ic流过电容时,在电容两端产生变化的电压
(4)
其中:Q为电量;C为电容的容量.设ton为开关管导通时间,toff为开关管关断时间,图2中,t1=ton,t2=ton+toff.对图2中的ic积分,其中积分下限为ton/2,积分上限为ton+toff/2.Δic=ΔIL,纹波电压Vrp为
(5)
可见增大f和C能降低纹波.
1.3电感计算
Buck变换器工作在CCM与断流工作模式(DCM)的临界电感Lc[6]如式(6)所示.
(6)
当L>Lc时,变换器工作在CCM模式.当f为定值,设计电感时Vo应取最小而R应取最大,最小Vo=0.1 V,最大R为假负载R1.
一般而言,电感值变大,输出纹波会变小,但电源的动态响应也会相应变差,所以电感值的选取可以根据电路的具体应用要求来调整以达到最理想效果.开关频率的提高可以让电感值变小,从而让电感的物理尺寸变小,节省电路板空间,目前的开关电源有往高频发展的趋势,以适应电子产品的体积越来越小的要求,所以电感值应该控制在毫亨级.综合考虑,假负载R1取200 Ω,计算后取L=1 mH.
1.4电容的计算
结合式(3)和(5),并考虑纹波电压的要求,有
(7)
因此,C取典型值470 μF.
2 Buck变换器建模与仿真
2.1Buck电路控制模型建模
Buck变换器有两种工作状态:开关管导通模式和开关管关断模式,等效电路分别如图3(a)和3(b)所示.
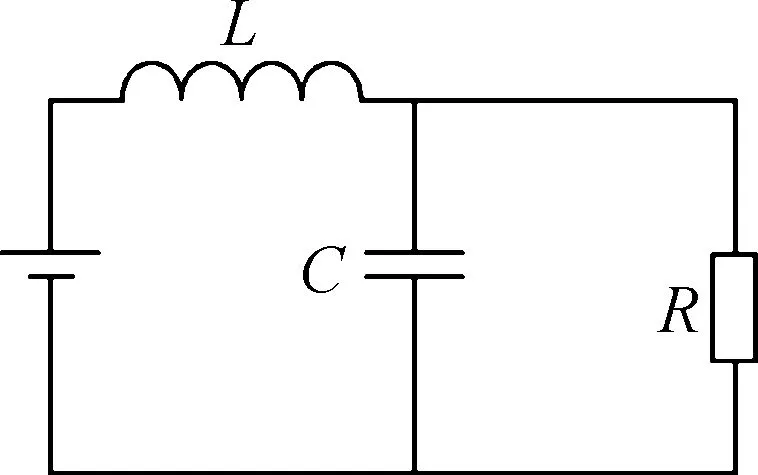
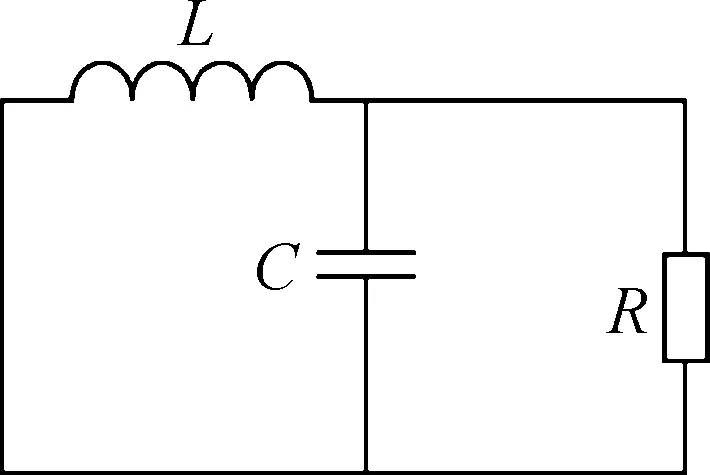
(a) 导通 (b) 关断图3 等效电路Fig.3 Equivalent circuit
由状态空间平均法得到Buck变换器的状态平均方程[7]如式(8)所示.
(8)
其中:u为控制信号.
Buck控制电路结构图如图4所示.

图4结构图
Fig.4Structure chart
Vo(s)=G(s)ViD(s)
(9)
其中
(10)
E(s)=Vref(s)-Vo(s)
(11)
式中:kp为比例系数;ki为积分系数;kd为微分系数.
根据劳斯系统稳定性判据[8],令kd=0,有
(12)
比例增益越大,调节灵敏度越高,所以取kp=10,代入式(12),得ki<106,又考虑到积分系数偏大时,系统震荡次数加大,工程经验上ki一般不大于kp,所以取ki=2.
2.2Buck电路仿真
根据Buck电路状态方程及电路控制系统模型建立变换器仿真模型.其中UC3842是一种性能优良的电流控制型脉宽调制芯片,该调制器单端输出,能直接驱动双极型功率管或者场效应管.图5为Buck电路仿真模型.

图5 电路仿真模型Fig.5 Circuit simulation model
在输出电压为10 V和输出电流为15 A的情况下,输出电压时域波形如图6所示.

图6 输出电压时域波形Fig.6 Output voltage time -domain
由图6可知,系统能稳定输出并且纹波电压约为0.000 2 V,与式(5)计算值一致.
此时电压波形在一个周期内变化一次.取输出电压和电感电流作相轨图,可以得到系统的吸引子,此时系统的吸引子为一条闭轨,如图7所示.
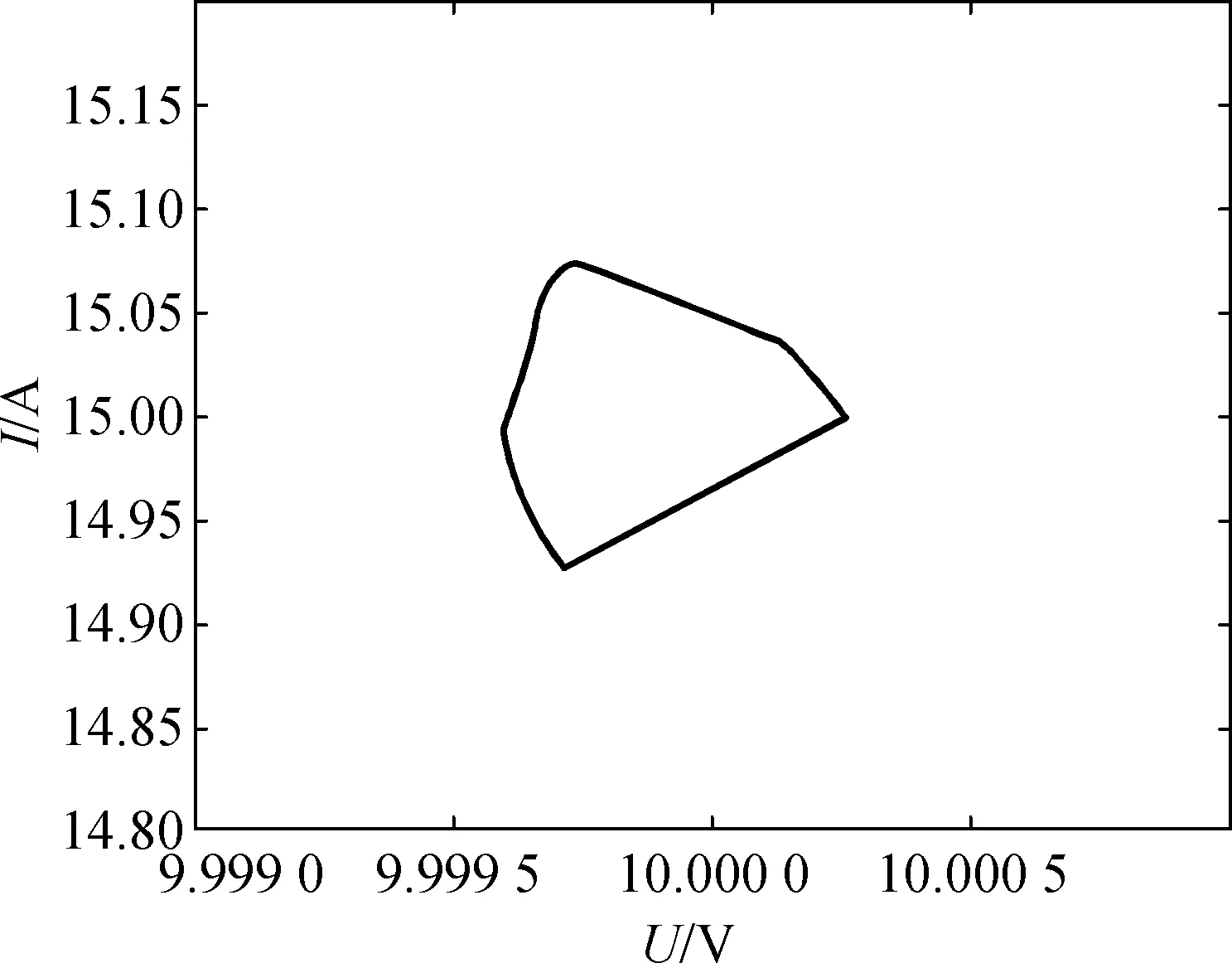
图7 相轨图Fig.7 Phase trajectory
3 分岔现象研究
分岔现象与非线性系统密切相关,系统参数、运行参数的变化都可能导致系统的不稳定运行.
在输出电压为10 V的情况下,上文中输出电流为15 A时,系统稳定且纹波达到理论值.在输出电流分别设为10 A和3 A,其他参数保持不变的情况下,对系统进行仿真.图8为相应的输出电压时域波形图与相轨图.
由图8可知,当输出电流为10 A时,输出电压的变化周期由原来的一个周期变为两个周期.由此可知,当输出电流从15 A变化到10 A的过程中,发生了倍周期分岔现象,系统的吸引子仍然是一条闭轨,但是闭轨周期变为原来的两倍.
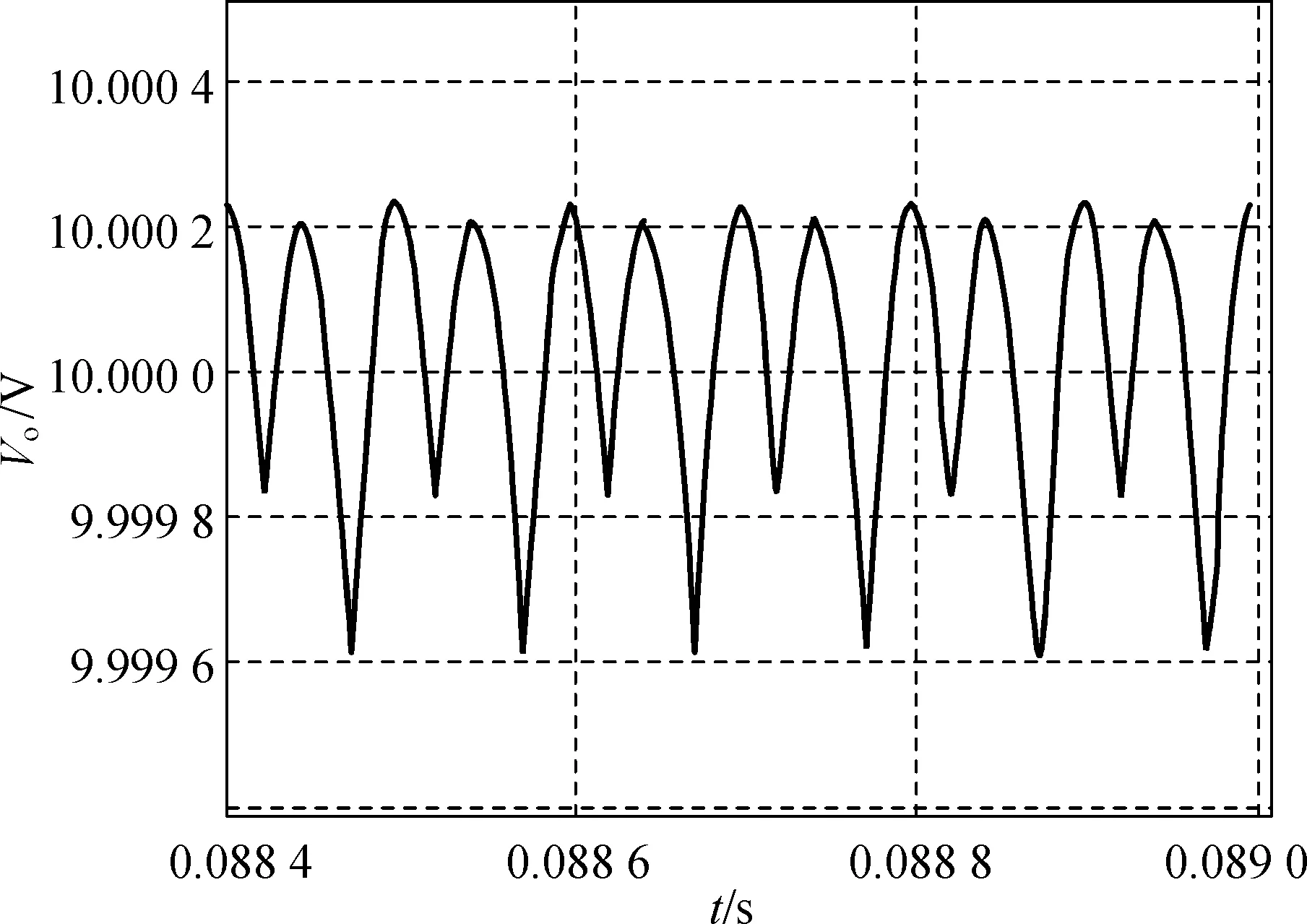
(a) 输出电流为10A时的时域波形图
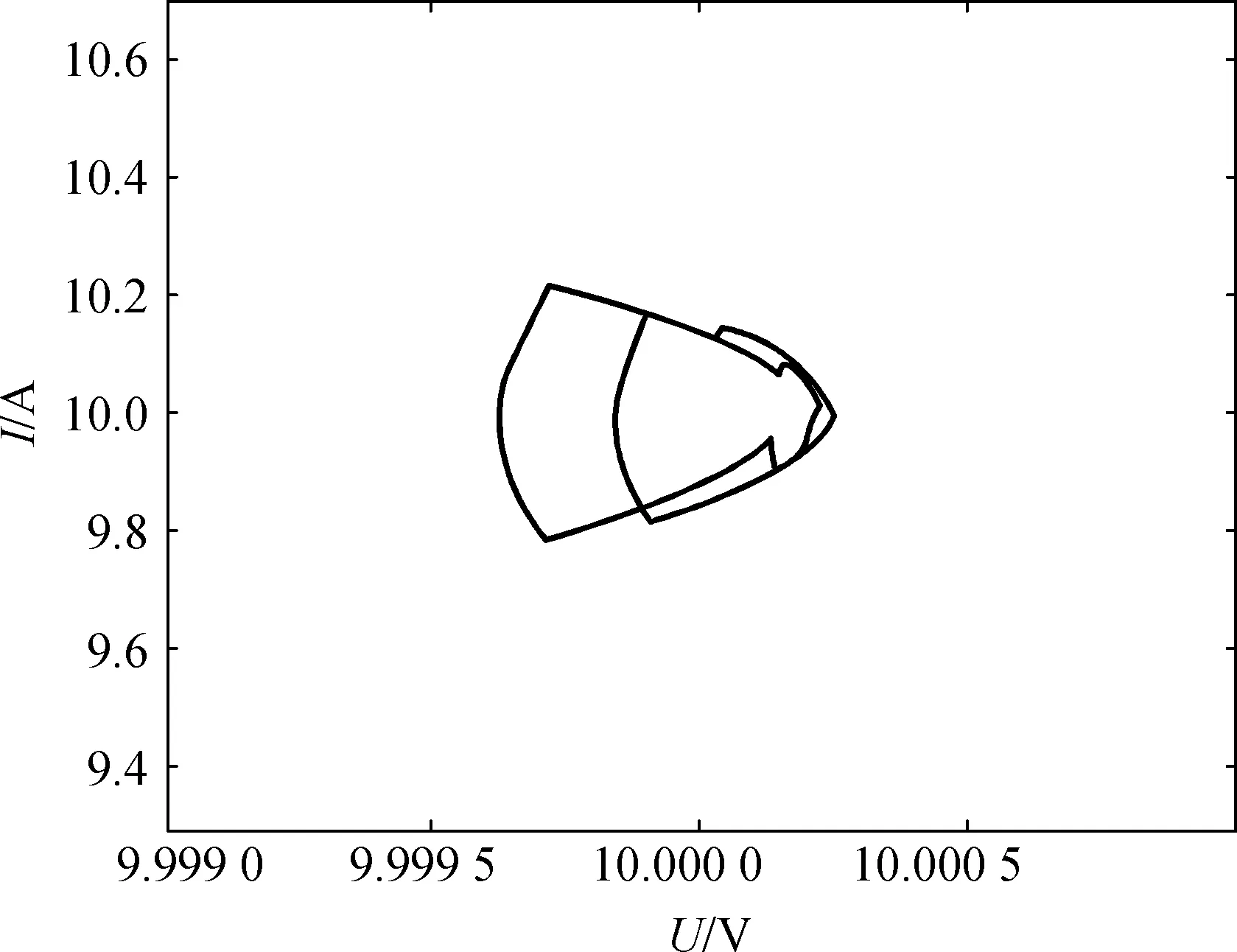
(b) 输出电流为10 A时的相轨图
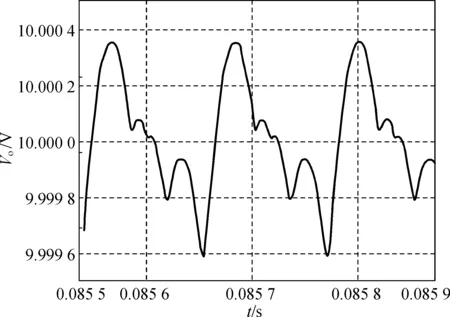
(c) 输出电流为3 A时的时域波形图
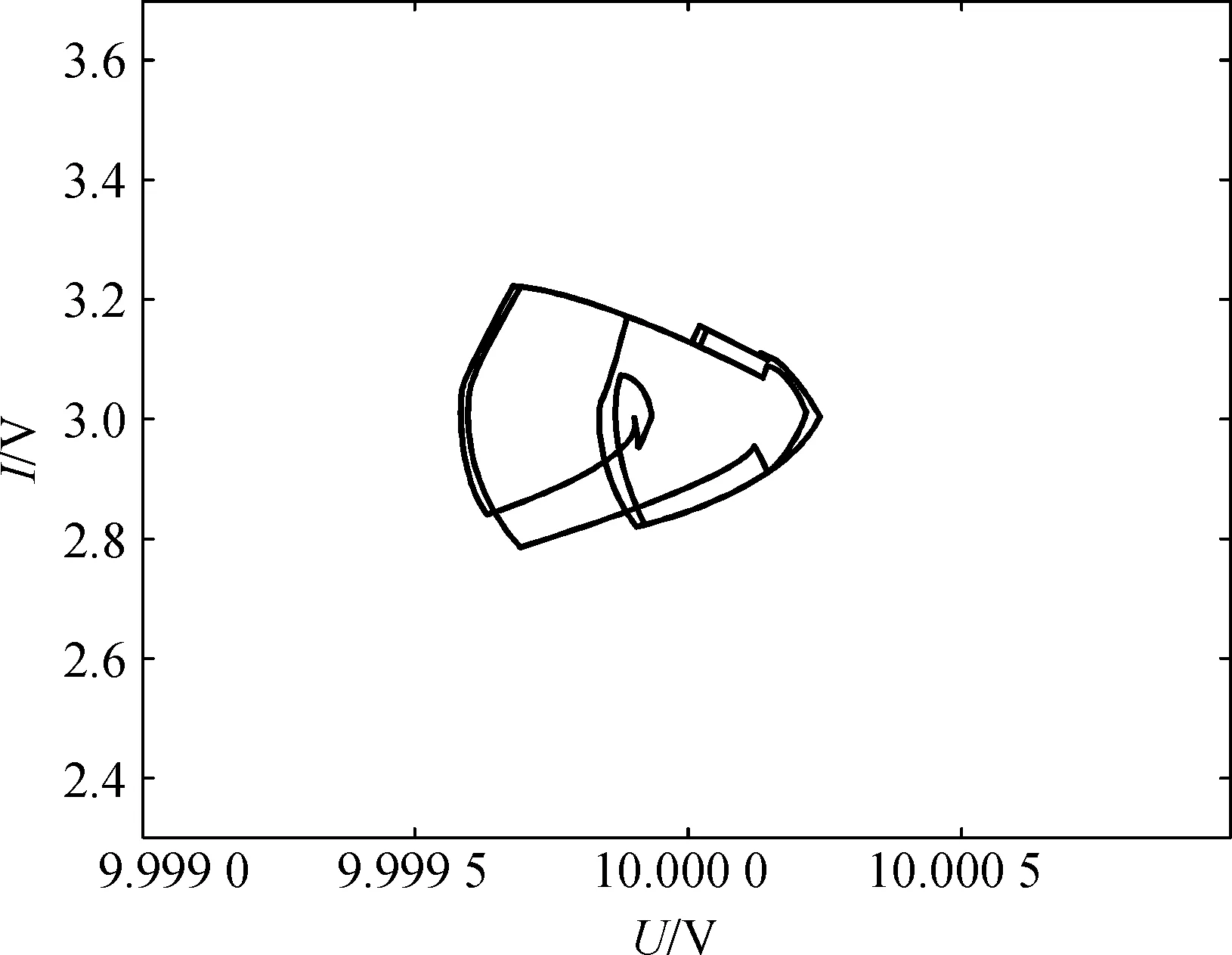
(d) 输出电流为3 A时的相轨图图8 输出电压时域波形和相轨图Fig.8 Output voltage time-domain and phase trajectory
当输出电流从15 A变化到3 A,在此期间发生了4倍周期分岔现象,系统的吸引子仍然是一条闭轨,但是闭环的周期变化为原来的4倍.
在输出电流为10 A时便发生了分岔现象,输出电压的纹波约为0.006 V,其纹波值大幅增大,远超理论值.分岔对输出纹波产生不利影响.
4 PWM有延迟的输出结果比较
由于UC3842输出PWM波时,高低电平变化并非瞬间发生,故无法输出低占空比.根据UC3842手册描述,上升时间和下降时间需要50~150 ns,取其平均值,认为至少有100 ns的高电平时间,对于100 kHz的开关频率,其最小占空比为1%.当输入电压为63 V时,理论上输出电压根据式(13)推算.
Vo=DVi
(13)
推算最小输出电压为0.63 V.
设定输出电压为2.0,1.0和0.1 V时,在输出电流为1 A情况下,通过仿真得到电压输出的波形如图9所示.由图9可以看到,由于PWM存在输出延迟,当设定电压为0.1 V时,最终稳定的电压却在0.6 V左右.
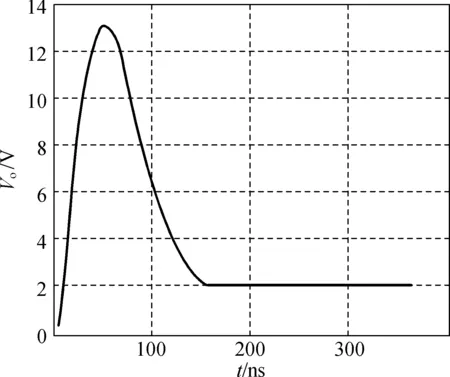
(a) 2.0V
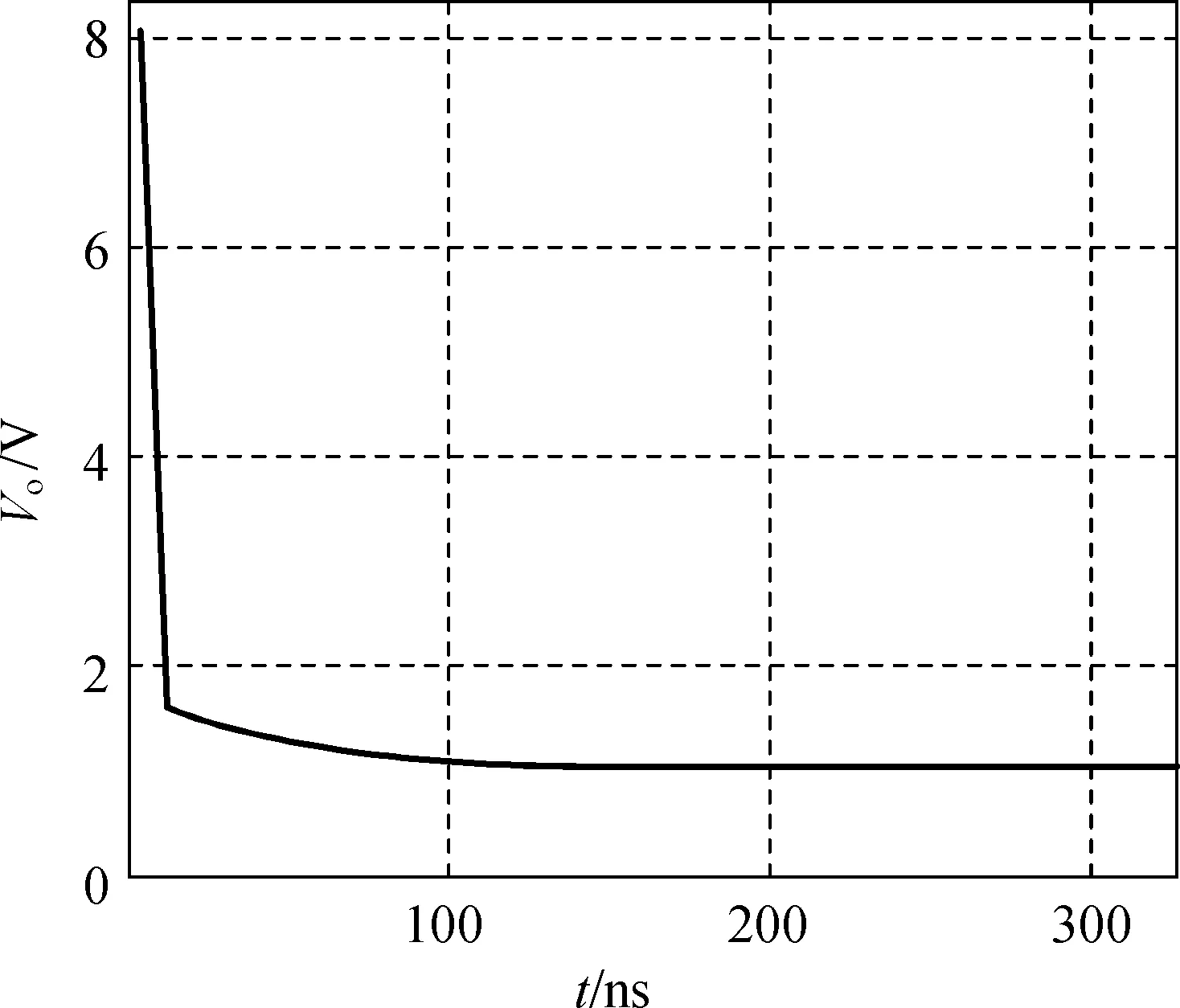
(b) 1.0V
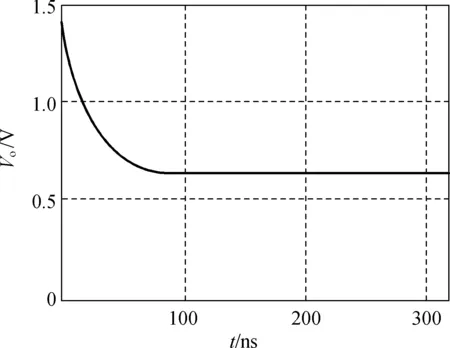
(c) 0.1 V图9 输出电压图Fig.9 Output voltage
综上所述,当输出低电压且PWM有延迟时,电源无法达到低电压,最低只能达到0.6 V左右的输出电压.
5 结 语
本文研究了宽范围输出的Buck电路,给出了CCM模式下电路主要参数的确定方法,并对其控制模型进行建模.通过仿真,指出了由于PWM控制芯片的延迟,限制了最小输出电压,以及分岔对输出纹波会产生不利影响,为后续深入研究打下基础.
[1] BROWN M.开关电源设计指南[M].徐德鸿,等译.2版.北京:机械工业出版社,2005.
[2] 杨俊伟,刘文剑.宽范围输出下DC-DC能量变换器的控制策略的研究与实现[J].应用能源技术,2011(7):47-50.
[3] 孙鹏菊,周雒维,杜雄.具有恒功率特性的输出宽范围可调的变结构DC-DC变换器[J].中国电机工程学报,2002,32(6):81-89.
[4] CHEN J X,ZHU J G,GUO Y G.A unified hybrid model with two level networks for pesk current-mode controlled bulk-boost DC to DC converters operating in DCM and CCM[C]//Conference on Electrical Machines and Systems.2007: 186-190.
[5] CHEN J X,GUO Y G,ZHU J G.A unified discrete model for PWM switching DC to DC converters with current-mode control[J].Australian Journal of Electrical and Electronics Engineering,2008,4(1): 63-72.
[6] 张占松,蔡宣三.开关电源的原理与设计[M].北京:电子工业出版社,2004.
[7] 宋受俊,刘景林,张智慧.BUCK变换器建模及其先进控制方法仿真[J].计算机仿真,2006,23(3):239-300.
[8] 张桢阳.大变比直流变换器若干关键技术问题研究[D].上海:东华大学机械工程学院,2011.
Several Key Technologies on Buck Converter in Application Field of Wide Range Output Voltage Regulation
CHENJia-xin,PENGXiao-long,HUAHua,LINYi
(College of Mechanical Engineering,Donghua University,Shanghai 201620,China)
Based on analyzing the ripple change characteristics of Buck converter,algebraic expressions of circuit main parameters and design technique of control system were proposed in continuous conducting mode.By using system simulation,the result shows that the bifurcation characteristics influence the output ripple of the converter,and the switch time delay makes the converter unstable when the output voltage is very small.Key words: Buck converter; ripple; continuous conducting mode(CCM); stability; bifurcation characteristics
1671-0444(2015)02-0237-05
2013-12-06
陈家新(1968—),男,安徽宣城人,副教授,博士,研究方向为电力电子、电机设计及其智能测控技术.E-mail: chjiaxin@dhu.edu.cn
TN 752
A

