模糊PID控制器在石灰窑温度控制系统中的应用

王丽华

(中国恩菲工程技术有限公司， 北京 100038)

模糊PID控制器在石灰窑温度控制系统中的应用

王丽华

(中国恩菲工程技术有限公司， 北京 100038)

石灰窑的温度控制受外界许多多变参数的影响，传统PID不能满足控制要求。采用模糊PID算法，将窑尾温度的偏差及其变化作为输入变量，重油流量调节阀的流量变化作为输出变量，经系统仿真得出，模糊PID控制能达到良好的控制效果，可缩短过程控制的调整时间，窑尾温度有较好的鲁棒性。

石灰窑； 模糊PID； 温度控制

0 前言

PID控制器因稳定性高、结构简单、操作简便在工业控制领域得到广泛应用。但常规PID控制器是建立在被控对象精确模型的基础上，而回转窑的生产过程存在众多干扰因素，如：重油流量、物料重量、石灰石的分解率及外界温度。不仅如此，其复杂的物理化学反应过程还具有超调量大、滞后时间长等问题。当生产中任一因素发生变化时，常规PID控制必须重新整定，显然不能满足实时高效的生产需求。本文根据回转窑工艺特点和控制要求，提出了基于模糊PID的窑温控制方法，以解决回转窑的控温精度问题。

1 模糊PID控制原理

模糊PID的结构形式就是用条件和结果形式即IF和THEN的模糊规则去替代相关的操作经验和技术，而这样形成的规则以及如PID初始值这类参数就被存入数据库中。再利用这些数据将原有PID的相关参数在线修改为满足模糊控制规则的形式，按这种方式构成的控制器称为模糊PID控制器。这种控制器能够以输入误差(e)以及误差变化(ec)，实现每一时刻e和ec的控制器参数自整定。其结构如图1所示。

图1 模糊PID控制器结构

具体说，PID参数模糊自整定是找出PID 3个参数(kp、ki、kd)与e和ec之间的模糊关系，在运行中不断改变e和ec，来对3个参数进行在线调整，以满足不同e和ec的要求，而使被控对象始终处于稳定可靠与实际接近状态。

2 论域、量化因子、比例因子的选择

本文采用二维模糊控制器结构形式，选取回转窑的温度偏差e和偏差变化率ec为输入量，设模糊语言变量分别为e，ec。输出量PID参数的修正量为kp，ki，kd。通过以往经验确定其论域：

e，ec={-3，-2，-1，0，1，2，3}；
kp={-1.2，1.2}；
ki={-0.6，0.6}；
kd={-3，3}；

划分等级与e，ec相同。

其模糊子集为e，ec={NB，NM，NS，ZO，PS，PM，PB}。

子集中各元素分别代表负大，负中，负小，零，正小，正中，正大(下文同)。

设e，ec和kp，ki，kd均服从高斯正态分布，得出各模糊子集的隶属度，根据e，ec，kp，ki，kd的量化论域，分别选择高斯隶属度函数的中心点和函数曲线的宽度。

3 建立模糊规则表

(1)比例系数kp在控制过程中采用如下方法：初期，将kp调整到较大来提高相应速度；中期，考虑到稳定性与调节精度，再适当放大kp；后期，为提高控制精度减小静差，将kp调整到较大档。比例系数kp的模糊规则见表1。

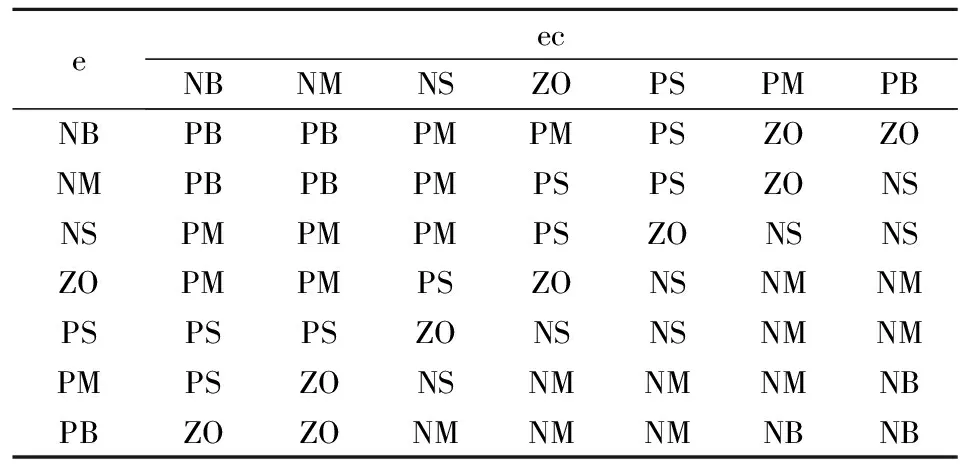
表1 kp的模糊规则表

(2)积分系数ki在控制过程中采用如下方法：初期，ki应弱一些;中期，保持系统稳定，ki应调整适中；后期，减小调节静差，增强ki。积分系数ki的模糊规则见表2。

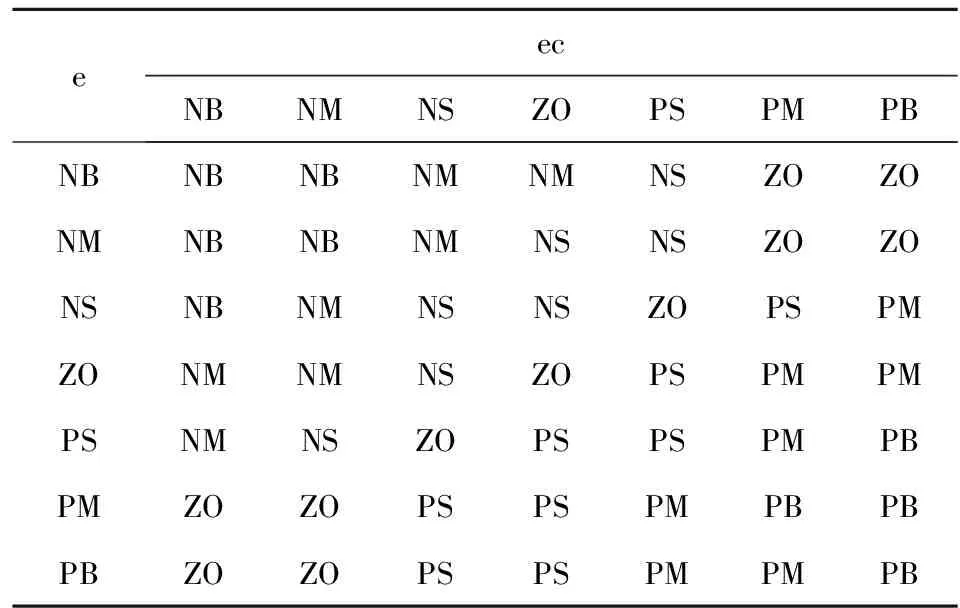
表2 ki的模糊规则表

(3)微分系数kd在控制过程中采用如下方法：初期，加大kd避免超调；中期， 调节特性对kd的变化比较灵敏，kd应适当小并保持不变；后期，kd减小，以便缩短调节时间。微分系数kd的模糊规则见表3。

表3 kd的模糊规则表

该规则库有3个子规则库组成，每个子规则库有双输入单输出组成，且每个子规则库互相独立，共有49条模糊规则，对kp、ki、kd进行在线自调整[1]。

4 模糊PID控制器在石灰窑温度控制系统中的应用研究

4.1 石灰窑温度控制系统设计

在活性石灰生产过程中，窑温必须保证维持在一定范围内波动，否则会出现生烧或过烧情况。在实际生产中，输入的重油流量、物料成分及重量、石灰石的分解率和外部温度等因素都对窑尾温度有影响，其中又以重油流量为主要影响因素。在工程中，通过调节安装在重油管道上的流量调节阀的阀门开度来进行流量控制。由此得出石灰窑煅烧的温度控制设计如图2所示。

图2 温度控制系统结构图

其中设窑尾温度为被控参数，调节阀的开度为调节器的输出控制参数；T0、η分别为外部温度和石灰石的分解率。

4.2 温控过程的数学模型

结合工程实践经验，根据石灰窑温度达到一定时会保持不变这一特征，并且考虑到重油在管道输送中存在的延迟现象，选择整个温度控制系统被控对象的近似模型为[2]:

G(S)=G1(S)G2(S)e-τs=K1K2e-τs/(TS+1)

(1)

式中：K1、K2为石灰窑温度的放大倍数，T为石灰窑温度的时间常数，τ为石灰窑温度的延长时间。

4.3 控制系统仿真的结果

在此仿真系统中，取石灰窑的各项参数(如重油燃烧值、重油密度等)进行仿真计算[3]，得出：

K1K2=1.26×86.40=108.864

(2)

由众多生产实践个案总结出，如果改变重油流量，需要大约10 s的管道传输时间才能影响到窑尾的温度，即在建模中系统存在10 s的纯滞后，因此，仿真模型为:

G(S)=108.864e-10s/(162.5S+1)

(3)

其中增益系数为108.864；时间常数T为162.5 s；滞后时间τ为10 s。

仿真过程中，采样时间为0.1 s， 当系统输入量是幅值为1的阶跃信号时，分别采用常规PID控制和模糊PID控制，得到如图4、图5的仿真结果。由图4、图5看出，模糊PID控制器对温度的跟踪效果较好，当在t=350 s加入阶跃干扰时，模糊PID控制器也能使系统保持良好的稳定性，快速地进入稳态且系统波动很小。总体来说，采用模糊PID控制时，系统的响应速度变快，精度的稳定性也得到了改善，仿真结果表明参数规则表合理，基本满足了焙烧温度曲线的控制要求。通过仿真，还观察到模糊控制系统的构成，如图6。

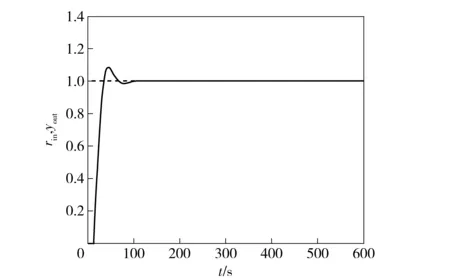
图4 常规PID控制阶跃响应

图5 模糊PID控制阶跃响应

模型系统包含：2个入口，3个出口，49个规则图6 模糊PID控制系统构成

5 结束语

在PID模糊理论基础上，结合工程实践经验，针对回转窑非线性、惯性大、纯滞后等问题,提出了窑温解决控制方法。对比例、积分、微分系数进行整定,建立模糊规则表。在满足石灰石生产的技术要求下，建立数学模型并且仿真，结果表明与常规PID相比，模糊控制PID的调整时间为100 s，是常规PID调整时间120 s的5/6，具有响应速度快、稳态精度高等优点，适用于类似回转窑之类的大时滞、大惯性的复杂工况。

与此同时，由于本文仿真所选模型为典型的一阶和二阶加滞后的形式，在模型选取上存在不准确性，对实际应用中的各种影响因素也不能完全考虑周全。因此，今后有必要在控制对象的非线性、多噪声干扰以及大时延等相关问题上进行更深入的研究。

[1] 吴胜彪，王祖麟，肖敏. Smith预估自适应Fuzzy PID控制器在乳化液温度控制系统中的设计[J]. 有色设备，2012(1)：27-31.

[2] 刘金琨.先进PID控制MATLAB仿真(第3版)》[M]. 北京：电子工业出版社，2011.

[3] 王丽华．回转窑模拟PID控制[C]．北京工业大学，2007．

ApplicationofFuzzyPIDControllerinLimeKilnTemperatureControlSystem

WANG Li-hua

Since the lime kiln temperature control is affected by various parameters outside, the traditional PID controllers cannot match it. Fuzzy PID calculation which using deviation and variation of kiln tail temperature as input variable, flow variation of heavy oil control valve as output variable, is adopted in this paper. After the simulation, fuzzy PID controller can get a favorable result: the adjusting time of process control is shortened and the robustness of kiln tail temperature is better.

lime kiln; fuzzy PID; temperature control

2014-10-21

王丽华(1982—)，女，安徽合肥人，大学本科，工程师，主要从事工业自动化设计工作。

TP273.4

A

1008-5122(2015)01-0038-04