基于改进核主成分分析的故障检测与诊断方法

韩敏，张占奎

（大连理工大学电子信息与电气工程学部，辽宁 大连 116023）

引 言

复杂工业过程如果发生故障，会造成巨大的损失，在线监控工业过程的运行状态，及时发现和识别故障至关重要。故障诊断主要研究如何对系统中出现的故障进行检测和辨识，也就是判断故障是否发生和故障发生的类型。其中，基于数据驱动的多元过程统计方法不需要精确的数学模型和先验知识，只需要对历史数据进行特征提取，在特征空间中构建监控统计量实现故障检测，并且根据贡献图识别引起故障的变量，是故障诊断领域研究的热点方向之一[1-3]。

特征提取作为非常关键的一步，直接影响故障检测与故障诊断的性能。一般来说，数据结构特征包括全局结构特征和局部结构特征。全局结构描述过程数据的整体结构，反映数据的外部形状，而局部结构描述过程数据近邻点的排列情况，反映数据的内在属性[4]。故障诊断中特征提取主要的手段包括：主成分分析（principal component analysis，PCA）[5]、偏最小二乘（partial least squares，PLS）[2]和独立成分分析（independent components analysis，ICA）[6]等。主成分分析通过求解历史数据协方差矩阵的特征值和特征矢量实现特征提取，由于主成分分析是一种线性投影方法[7]，无法解决过程监控中的非线性问题。为克服这一缺陷，核主成分分析（kernel principal component analysis，KPCA）被提出[8]。核主成分分析通过非线性映射函数将历史数据从原始空间投影到高维特征空间再运用线性PCA 技术，保留原始数据中大部分方差信息，但方差主要描述的是样本空间的全局结构信息[4]。最近，研究表明流形学习（manifold learning）能够提取数据集在原始变量空间中隐藏的局部结构，受到过程监控领域的关注[9-11]。流形学习主要方法包括拉普拉斯特征映射法（Laplacian eigenmaps，LE）[12]，局部线性嵌套法（locally linear embedding，LLE）[13]，局部保持投影法（locality preserving projections，LPP）[14]等。其中，局部保持投影法在保持局部结构的同时实现了线性计算，得到广泛的应用，并且通过引入核方法提出了核局部保持投影（kernel locality preserving projection，KLPP）[15]。然而，在特征提取过程中丢失局部结构或者全局结构都会影响特征提取的效果。因此，一些综合保持全局结构和局部结构的方法不断地被提出，例如global-local structure analysis（GLSA）[4]、local and global principal component analysis（LGPCA）[16]、tensor global-local structure analysis（TGLSA）[17]等。但这些方法本质上是线性投影方法，不能有效地提取工业过程中的非线性特征。

在故障检测与诊断问题上，传统方法采用T2统计量和平方预测误差（squared prediction error，SPE）统计量两个监控指标判断是否有故障发生，并且根据贡献图辨识引起故障的变量[1]。T2指标采用马氏距离作为度量，而SPE 指标采用欧式距离作为度量，导致这两个统计量不能联合起来进行故障检测，并且通过两个指标分别得到的贡献图无法准确诊断出发生的故障类型[18]。由于过程监控的任务是从大量的样本数据中区分出正常样本和故障样本，因此故障检测可以认为是分类问题。其中，费舍尔判别分析（Fisher discriminant analysis，FDA）作为一个经典的维数约减和模式分类方法，被广泛应用。例如，He 等[19]通过使用故障模式类标签知识建立故障分类模型，在此基础之上，Zhang 等[20]使用费舍尔判别分析求解满足最大分离度的特征矢量和判别矢量来实现状态监测，提高了系统故障检测与诊断能力。

为解决传统核主成分分析提取非线性特征时只考虑过程数据全局结构而忽略局部结构特征的缺陷，本文将核局部保持投影方法保持局部近邻结构思想融入到核主成分分析的目标函数中，提出一种改进核主成分分析方法（modified kernel principal component analysis，MKPCA），解决工业过程中数据变量存在非线性关系的问题。该方法既能够保持数据集整体方差的最大化，又可以保持数据集局部近邻结构不变。本文将所提方法用于过程数据降维和特征提取，并与费舍尔判别分析相结合，将获得的特征信息分类，以判别矢量的欧式距离为统计量检测故障，并且根据特征矢量间的相似度系数快速识别故障类型。

1 改进核主成分分析方法

作为非线性特征提取的经典方法，核主成分分析（KPCA）通过非线性函数将输入数据集从原始空间映射到高维特征空间运用线性主成分分析技术进行特征提取，实现了方差最大化，但方差主要描述数据集的全局结构信息。另一方面，核局部保持投影（KLPP）是一种通过在核空间建立近邻图来保持数据集局部结构的方法，其本身着眼于局部结构的保持，并没有考虑全局结构特征。借鉴核主成分 分析和核局部保持投影方法的思想，本文提出改进核主成分分析方法（MKPCA），其优化目标可以分解为全局和局部两个目标函数。全局目标函数使映射得到的特征空间保留原始数据集的大部分方差信息，实现全局特征提取；局部目标函数使映射得到的特征空间和原始数据集具有相似的局部近邻结构，实现局部特征的提取。

1.1 核主成分分析

核主成分分析（KPCA）通过非线性映射函数将历史数据从原始空间投影到高维特征空间再运用线性PCA 技术，保留原始数据中大部分方差信息。假设已知数据集XT=[x1,x2,…,xn]∈Rm×n，m表示系统变量数目，n表示系统样本数目，定义从原始空间到高维特征空间的非线性映射φ，Jglobal(w)的目标是在特征空间中寻找一个投影向量w，使得投影后的yi=(φ(xi))Tw保留原始数据集的大部分方差信息，其中，i=1,2,…,n。核主成分分析的目标函数Jglobal(w)可以用式(1)表示

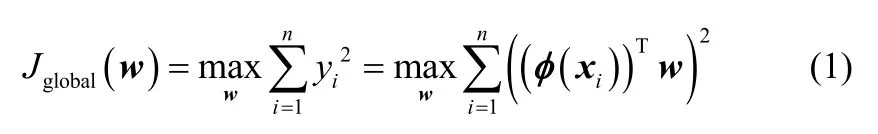
式中，wTw=1。

因为特征空间由过程数据的映射值φ(x1),φ(x2),…,φ(xn)组成，所以投影向量w必定在特征点φ(xi)展开方向上，即存在一个向量α=(α1,α2,…,α n)T满足

将式(2)代入式(1)，目标函数转化为求解α，如式(3)所示

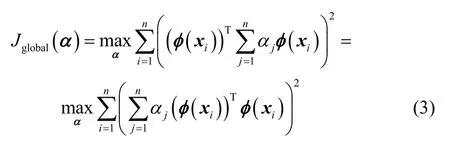
然后，为求解上述非线性问题，引入核函数K(i,j)=φ(xi)Tφ(xj)，可得核矩阵则目标函数可以转换为

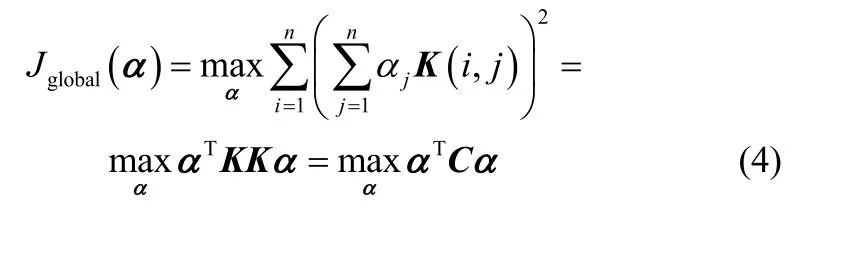
式中，αΤKα=1，C=KK。

核主成分分析的目标函数通过非线性函数将原始数据集映射到高维空间，因为在高维空间保留原始数据集的大部分方差信息，实现了全局结构的特征提取。但是，全局目标函数中并没有考虑不同样本点之间的内在关系，样本点之间的局部几何关系有可能被打乱，导致过程信息的丢失。

1.2 核局部保持投影

核局部保持投影（KLPP）通过在核空间建立近邻图，对邻域图各边赋加合理的权重，能够很好地表现数据集流形的局部结构。假设已知数据集XT=[x1,x2,⋅⋅⋅,xn]∈Rm×n，m表示系统变量数目，n表示系统样本数目，定义从原始空间到高维空间的非线性映射φ，Jglobal(w)的目标就是寻找投影向量w使得投影yi=(φ(xi))Tw在高维空间保持数据点之间的近邻关系，其中，i=1,2,⋅⋅⋅,n。也就是如果φ(xi)和φ(xj)是近邻，即ε为阈值参数，那么yi=(φ(xi))Tw和yj=(φ(xj))Tw也应该是近邻的。核局部保持投影的目标函数定义如下：

S为权重矩阵，D为对角矩阵，

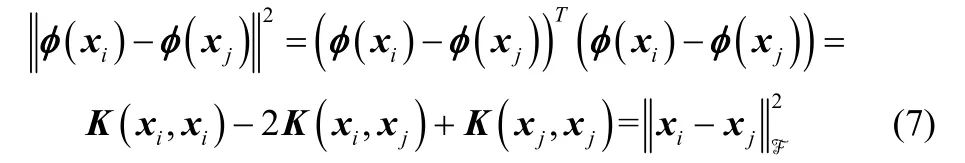
同样，存在一个向量α=(α1,α2,…,α n)T满足那么核局部保持投影的目标函 数为

式中，L=D-S是Laplacian 矩阵，L′=KLK。

核局部保持投影的目标函数通过在高维空间保持原始数据点之间的近邻关系，实现对原始数据集的局部结构提取。但是，其局部目标函数仅仅关注样本点之间的局部关系，并没有考虑样本点的全局特征。

1.3 改进核主成分分析方法

结合核主成分分析和核局部保持投影算法的优点，本文将核局部保持投影方法保持局部结构的思想融入核主成分分析的目标函数中，提出改进核主成分分析（MKPCA），使提取特征时得到的特征空间既能保留原始数据集的全局结构，又和原始数据集具有相似的局部近邻结构，克服传统核主成分分析方法只关注全局结构特征而忽略局部结构特征的缺陷。然而，这两个目标函数很难同时达到最优。针对该问题，引入参数η平衡这两个目标函数。改进核主成分分析的优化目标定义如下

式中，M=ηC+(1 -η)L′，αΤKα=1，0≤η≤1。

求解上述目标函数，必须要认识到不同的目标函数可能有不同的规模和收敛速度，因此，应选择适当的参数η来统一目标函数的规模，并且使它们具有相同的收敛速度。实际上，上述目标函数的优化问题最终转化为一个特征向量的问题来求解。由于没有采取迭代搜索的策略，在这里不会涉及收敛速度的问题，只需要考虑两个子目标函数之间规模的差异。受到参考文献[16-17]的启发，定义Jglobal(α)和Jlocal(α)的规模如下

式中，ρ(⋅)为相关矩阵的谱半径。为了统一全局和局部结构保持的不同规模，定义式(12)

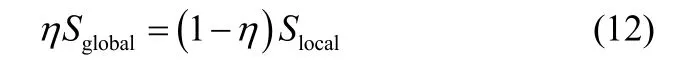
因此，参数η可以用下式求解

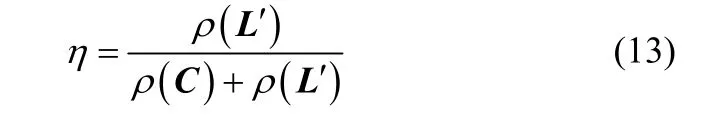
当确定η的值后，利用拉格朗日因子法求解α，最大化αTMα- λ(αΤKα- 1)，对α求导并令其等于0，最终推导出式(14)

因此，改进核主成分分析方法转化为求解方程(14)的广义特征值问题。为了解决非奇异问题，引入正则化的方法[9]，式(14)中将 +nβK Ⅰ代替K，其中，β为一个非常小的正整数，nⅠ为一个n n× 的单位矩阵。然后，得到按大小排列的特征值λ1,λ2,…,λn及与之对应的特征向量α1,α2,…,α n，进而得到投影矩阵Α=[α1,α2,⋅⋅⋅,α n]。根据特征提取后的能量保持率γ（通常取大于85%），即特征提取后需要满足

选取最大的d个特征值[λ1,λ2,…,λd]所对应的特征矢量α1,α2,…,α d构成Α′=[α1,α2,…,α d]。另外，使用改进核主成分分析方法时涉及核矩阵K的去中心化处理[21]。

基于改进核主成分分析方法的特征提取步骤如下：

（1）给定正常工况下的训练数据，进行归一化，得到原始数据集XT=[x1,x2,⋅⋅⋅,xn]；

（2）选择适当的参数，确定原始数据集的核矩阵K和矩阵L；

（3）求解式(14)，得到投影矩阵Α=[α1,α2,⋅⋅⋅,α n]；

（4）按照式(15)选择合适的主成分个数，投影矩阵Α′=[α1,α2,⋅⋅⋅,α d]；

（5）按照T=KTΑ′，提取数据集XT的特征。

2 费舍尔判别分析方法

费舍尔判别分析（FDA）是一种通过确定满足类间离散度最大化和类内离散度最小化的线性变换，来降低特征空间维数的模式分类方法，它可以最大程度地将各类数据分开[20]。设X∈Rn×m是一组由n个采样和m个测量变量构成的数据集，包含p类数据，nj为第j类数据的个数。令Sa为类内离散度矩阵，Sb为类间离散度矩阵。类内离散度矩阵为

式中，f为所求的最优投影矢量。求解如下广义特征值问题

求解式(19)可以得到n个特征值和与之相对应的n个特征向量，取前s个特征值对应的特征向量作为特征矩阵F，最大特征值对应的特征向量作为最优特征矢量fopt。

3 基于MKPCA-FDA 的故障检测与诊断

输入数据集之间差异越大，费舍尔判别分析方法的分类效果就越好。由于过程数据对象往往是高维、有噪声的，一般情况首先使用特征提取技术将原始输入空间映射到特征空间，而特征提取的效果会直接影响分类器性能。改进核主成分分析（MKPCA）作为一种特征提取方法，兼顾数据集的全局结构特征和局部结构特征，能够较好地保持数据集之间的差异信息，将提取的特征信息作为分类器的输入，可以提高分类器故障检测与诊断的能力。基于MKPCA-FDA 的故障检测与诊断方法通过MKPCA 提取正常工况下数据和各故障类别数据的非线性特征，使用FDA 建模，计算出特征矩阵和最优特征矢量，构建距离统计量并通过核密度估计确定其控制限，利用相似度的性能诊断方法识别发生的故障类型。

正常工况下训练数据的判别矢量和新采样测试数据的判别矢量分别为

式中，Ttrain和Ttest分别为MKPCA 提取的正常工况下训练数据和新采样测试数据的特征信息。将每一类数据的判别矢量看成一个簇，求取簇中判别矢量的均值确定正常工况下训练数据判别矢量的中心ξcenter，通过式(22)计算正常工况下训练数据的判别矢量ξtrain与中心ξcenter之间的欧氏距离

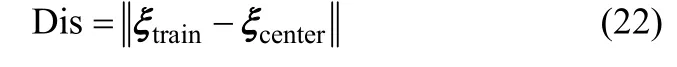
Dis 为正常工况下训练数据的监控统计量，通过核密度估计的方法[22]确定监控统计控制限Dis∗。当获取到新采样数据时，通过下式计算新采样数据的判别矢量ξnew与正常数据判别矢量中心ξcenter之间的欧氏距离

当计算出的新采样数据的统计量Disnew大于控制限Dis∗时，即可判断出有故障发生。检测到有故障发生之后，判断故障发生的类型。首先，离线确定各故障的诊断阈值。使用最优特征矢量建立故障诊断库，p为故障类的个数，计算各类故障之间的相似度，定义最优特征矢量与之间的相似度系数为 Simi,j，相似度系数Simi,j可以通过下式获得

每种故障的阈值是故障诊断库中不同于本故障的相似度的均值，通过式(25)计算可以得到第i类故障的诊断阈值

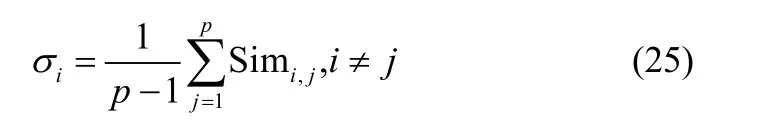
式中，p表示故障类个数。

当在线检测到故障后，计算新采样数据的最优特征矢量和故障诊断库里最优特征矢量之间的相似度系数为 Simnew,j，使用相似度系数Simnew,j来判断故障类型。如果新采样数据的最优特征矢量与故障诊断库里中第j个故障的最优判别矢量之间的相似度最大，并且超过了该类故障的诊断阈值，则判断为第j类故障发生。否则，将待测样本发生的故障类型认为是新的故障类型，更新故障诊断历史数据库。

传统方法采用T2和SPE 统计量检测故障是否发生。T2是当前采样数据主元向量的马氏范数，而SPE 表示主元模型对采样数据的平方预测误差，采用欧式距离作为度量。T2和SPE 统计量的不一致性，导致有时会得到不同的故障检测和诊断结果。本文在特征空间中使用FDA 建立监控统计量Dis，并且使用最优特征矢量快速识别故障类型。FDA 充分考虑到了故障分类信息，提高了不同类别子集间的分离程度，有利于提高故障检测和诊断能力。

基于MKPCA-FDA 的故障检测与诊断流程：

（1）收集正常工况下过程变量数据集和p类历史故障数据集；

（2）使用MKPCA 提取正常工况数据集和故障数据集的非线性特征Tnormal和Tfault；

（5）确定新采样数据判别矢量ξnew和正常工况下数据集判别矢量的中心ξcenter之间的欧氏距离Disnew。

（6）比较监控统计量 Disnew和监控统计控制限Dis∗，如果 Disnew＞ D is∗，判断有故障产生，然后，计算相似度系数，识别故障类型。

4 仿真实验

为验证本文所提方法的有效性，采用Tennessee Eastman（TE）过程故障检测数据集进行仿真实验。TE 过程[6]作为一个基于真实工业过程的仿真平台，在基于数据驱动的故障检测研究领域中被广泛应用于评价监控方法的性能。该过程有12 个操作变量和41 个测量变量，包含了正常状态及21 种不同状态的故障。本文使用的数据下载自http://web.mit.edu/ braatzgroup/links.html，选取33 个变量作为过程监测变量，每种状态的数据包括训练数据集和测试数据集，分别是480 组和960 组数据，每一种故障从第161 个数据点开始引入。

4.1 特征提取

为验证本文所提方法具有较好的特征提取效果，首先使用本文所提方法进行特征提取仿真实验。从训练数据集和测试数据中分别取1 组正常工况数据和3 组不同的故障数据（以故障4、故障8 和故障14 为例），使用本文所提MKPCA-FDA 方法将数据投影到特征矢量方向上，得到数据第一和第二特征矢量的分散图，并分别KPCA 方法、KLPP 方法、LGPCA 方法、GLSA 方法、FDA 方法和KFDA 方法进行比较。建立KPCA 模型时，选取高斯核函数其中，核参数σ=20m，m为过程变量的维数，采用方差累计百分比方法，确定主元个数为9。作为对照，同样设定其余方法的潜隐变量个数为9。采用k最近邻法来计算相似矩阵，其中，参数k=10，t=1。各方法的统计量置信限均选择为99%。

图1 基于KPCA 的特征提取Fig.1 Features extracted based on KPCA

图2 基于KLPP 的特征提取Fig.2 Features extracted based on KLPP

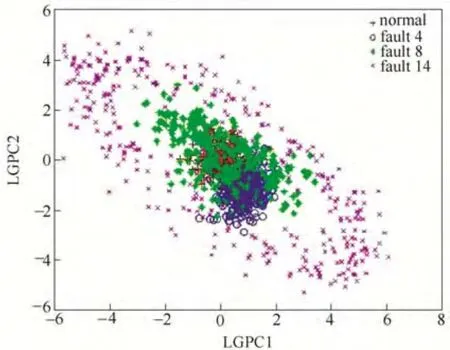
图3 基于LGPCA 的特征提取Fig.3 Features extracted based on LGPCA

图4 基于GLSA 的特征提取Fig.4 Features extracted based on GLSA

图5 基于FDA 的特征提取Fig.5 Features extracted based on FDA

从图1和图2KPCA 和KLPP 的前两维特征提取结果可见，KPCA 和KLPP 都无法将4 类数据有效地分离，特别是正常工况和故障4 存在大量的重合；图3和图4分别为LGPCA 和GLSA 的前两维特征提取结果，由于综合保持了全局结构和局部结 构，其效果要略好于前两种方法；图5为FDA 的前两维特征提取结果，只有故障4 被有效地区分开，正常数据、故障8和故障14并不能被有效地区分开；从图6中可以看出，非线性方法KFDA 能够将故 障4 和故障14 区分开，效果要好于线性方法 FDA，但是正常数据和故障8 仍有重叠；本文所提 MKPCA-FDA 方法的特征提取结果如图7所示，由于MKPCA 方法可以提取信息量更加丰富的数据作为FDA 方法的输入，本文方法在完成数据降维和可视化的同时能够将正常数据、故障4、故障8 和故障14 有效地分离，使得用判别矢量的欧氏距离作为统计量进行过程监控成为可能。

图6 基于KFDA 的特征提取Fig.6 Features extracted based on KFDA

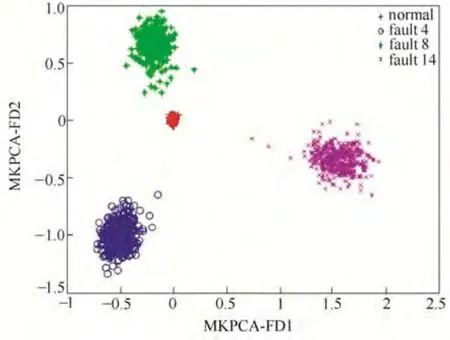
图7 基于MKPCA-FDA 的特征提取Fig.7 Features extracted based on MKPCA-FDA

4.2 故障检测

图8 KPCA 方法的故障5 监控结果Fig.8 Monitoring result of KPCA on fault 5

图9 KLPP 方法的故障5 监控结果Fig.9 Monitoring result of KLPP on fault 5

为验证本文所提方法的故障检测能力，以故障5 为例进行实验。故障5 是一个发生在冷凝器冷却水入口温度上的阶跃型故障，故障发生后冷凝器的冷却水流量会随之发生一个显著的阶跃变化，同时，从冷凝器出口到分离器的流速增加，进而导致气液分离器温度增加，分离器冷却水出口温度也随之增加。但是TE 仿真平台的控制回路能够通过反馈补偿这个故障变化，最终分离器中的温度降返回正常状态。这也使得一些监控方法只能在故障发生的初期检测到这类故障，而不能持续地给出报警。图8为基于KPCA 方法的2T和SPE 统计量的故障检测结果，两种统计量对故障5 的反应不敏感；从图9中可以看出，KLPP 方法的T2和SPE 统计量仍然无法有效地检测故障；图10为基于LGPCA 方法的T2和SPE 统计量的故障检测结果，SPE 统计量对故障5 的反应不敏感，T2能够持续检测出故障，但波动较大；从图11中可以看出，GLSA 方法的SPE统计量仍然无法有效地检测故障，而且T2的波动也较大；从图12中FDA 方法的检测结果可见，直接使用FDA 的效果仍不理想；图13为KFDA 方法的距离统计量检测结果，其效果要好于KPCA 方法和FDA 方法；本文所提方法对故障5 的检测结果如图14所示，在前160 采样时刻没有发生误报，在第161采样时刻距离统计量超过了监测控制限，而且能持续稳定地检测出故障。

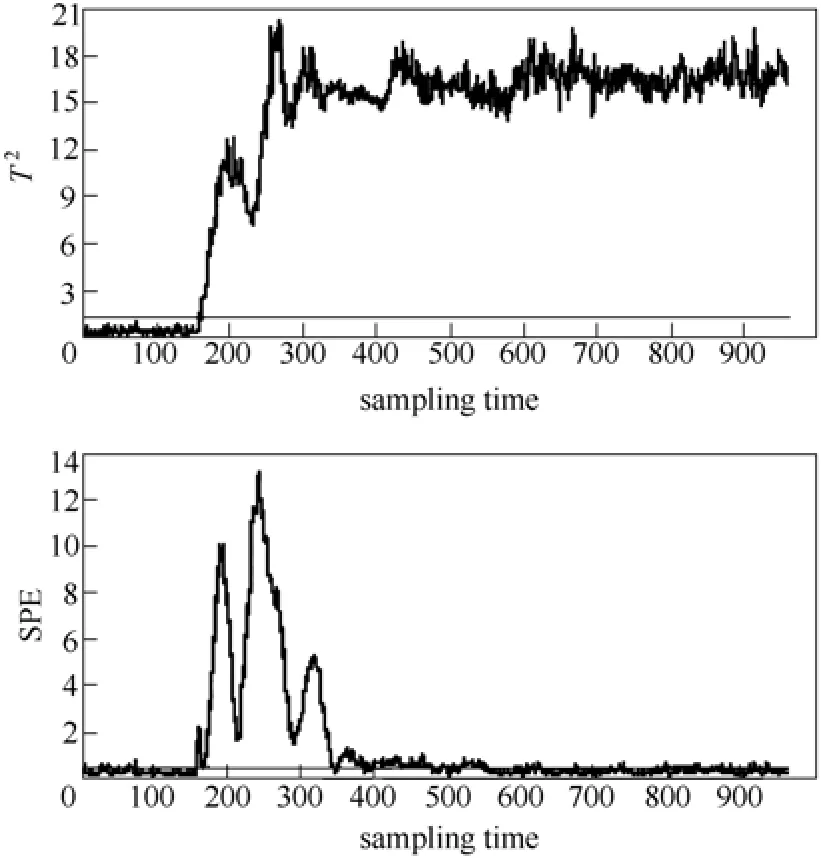
图10 LGPCA 方法的故障5 监控结果Fig.10 Monitoring result of LGPCA on fault 5

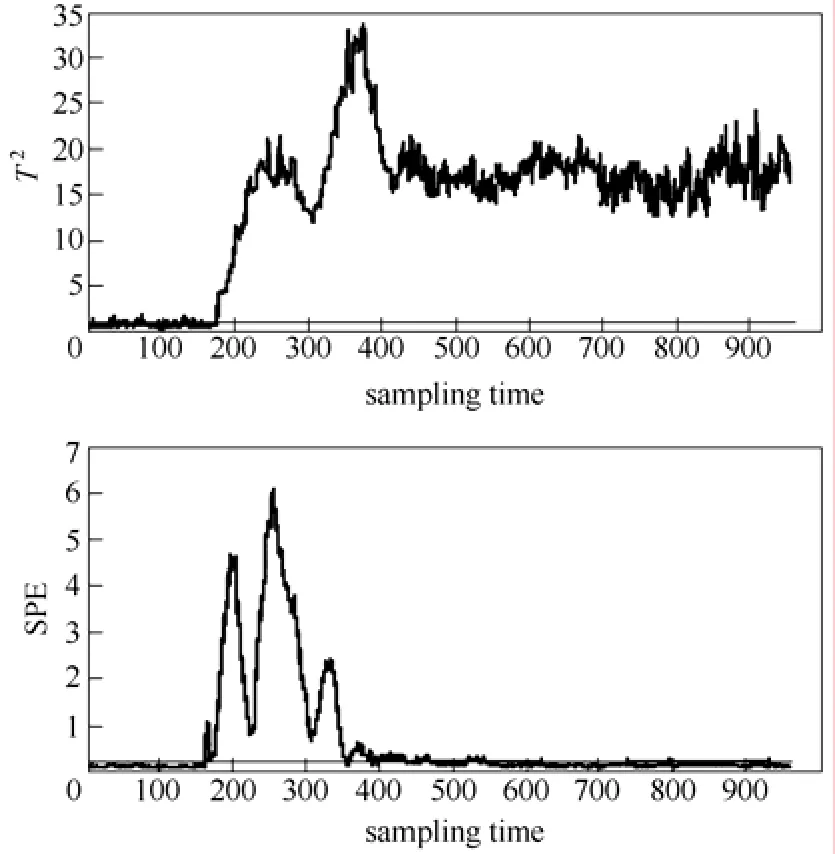
图11 GLSA 方法的故障5 监控结果Fig.11 Monitoring result of GLSA on fault 5

图12 FDA 方法的故障5 监控结果Fig.12 Monitoring result of FDA on fault 5

从表1中可以看出，本文所提方法在测试数据集中均取得了较好结果。KPCA 和KLPP 作为基本方法，其故障检测性能接近；LGPCA 和GLSA 方法，在进行特征提取时能够关注数据集的局部和全局特征，检测性能有一定的改善；作为一种有监督的非线性模式分类方法KFDA，利用了数据的类别信息，其故障检测性能要好于线性方法FDA；本文所提方法的故障检测效果最好，本文方法利用MKPCA 全面提取各数据的全局特征和局部特征，能够反映数据的内在属性，增大了数据间的差异，将之作为FDA 的输入，提高了FDA 分类的效果。

表1 故障检测率测试结果Table 1 Test results of fault detection rate

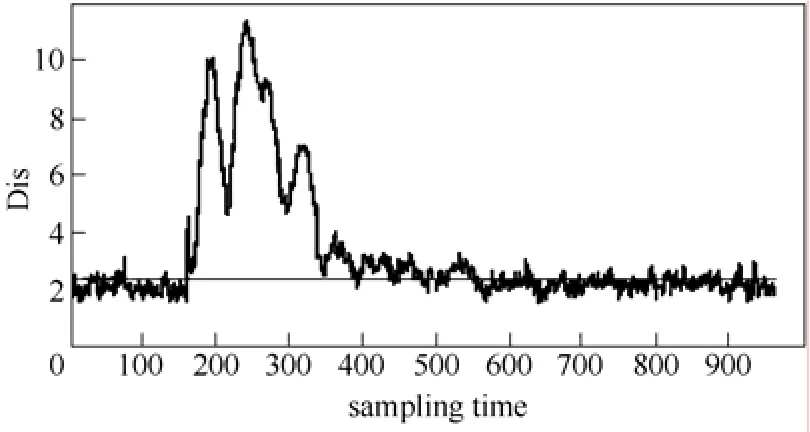
图13 KFDA 方法的故障5 监控结果Fig.13 Monitoring result of KFDA on fault 5

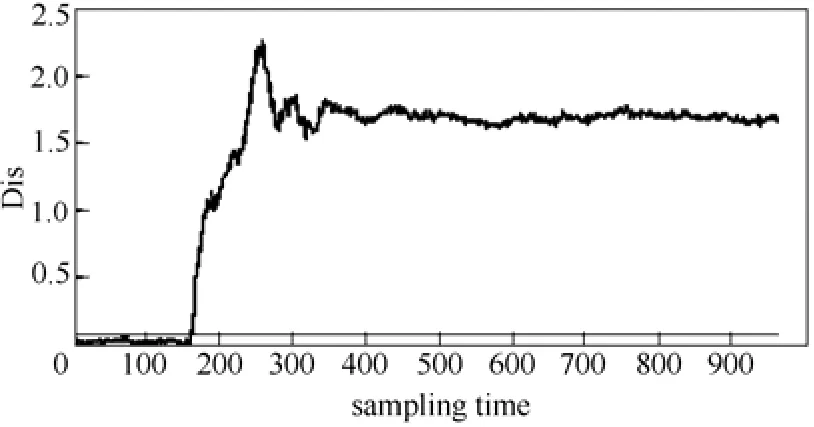
图14 MKPCA-FDA 方法的故障5 监控结果Fig.14 Monitoring result of MKPCA-FDA on fault 5

4.3 故障诊断

当系统成功地检测到故障后，需要判断发生的故障类型，本文使用相似度的性能诊断方法识别发生的故障类型。首先，离线确定各故障的诊断阈值。对TE 过程每种故障（共21 种）的480 组训练数据建立MKPCA-FDA 模型，得到每种故障类型的最优特征矢量，使用最优特征矢量建立历史故障诊断库，在建立历史数据故障诊断库的基础上，计算各类故障最优特征矢量之间的相似度系数值，最后，计算各故障的诊断阈值，每种故障的阈值是故障诊断库中不同于本故障的相似度的均值，如表2所示。

以故障5 为例，图15为本文方法在第161 时刻检测出故障后，利用最优特征矢量对故障5 的相似度分析，可以看出，在第161 时刻发生故障的最优特征矢量与故障诊断库中故障5 最优特征矢量的相似度系数值最大，且超过了故障诊断阈值，因此判断系统在第161 时刻所发生的故障类型为故障5，与实际情况吻合。

表2 各故障的诊断阈值Table 2 Diagnosis threshold of each fault

图15 故障5 的诊断效果Fig.15 Fault diagnosis effect diagram of fault 5

为可视化本文所提方法具有较好的故障识别效果，从表1中挑选了9 种故障工况，从故障诊断库中选择相应数据集的最优特征矢量，得到各测试数据集的特征矢量与故障诊断库中特征矢量的相似度系数，如图16所示，可以看到，本文所提方法能够将各种故障识别出来。

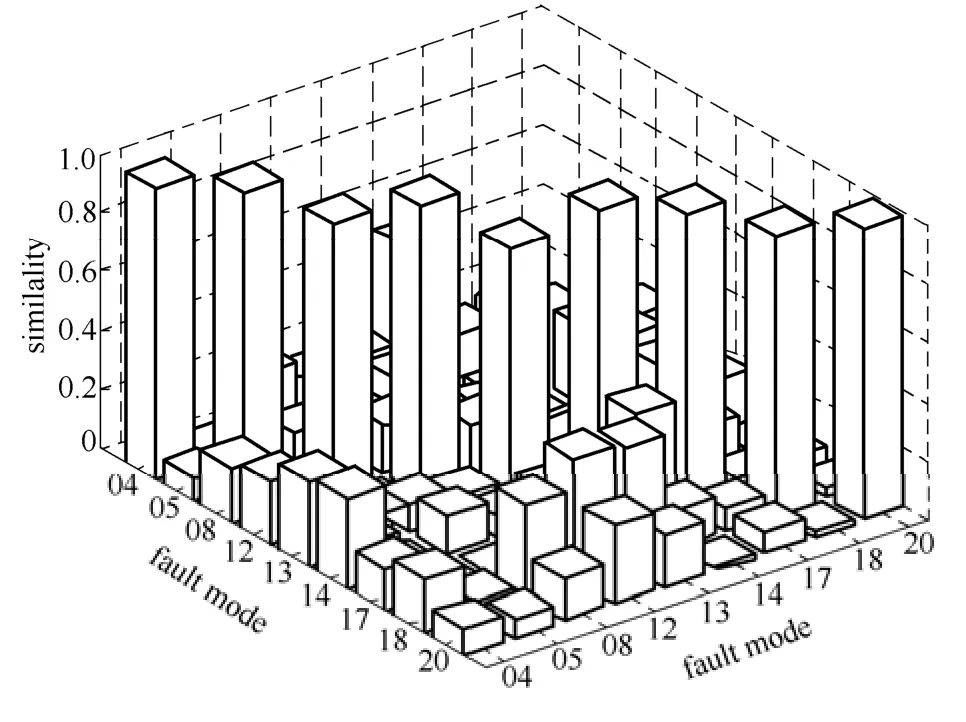
图16 9 种故障工况的识别结果Fig.16 Fault identification results among nine selected fault cases

5 结 论

本文针对传统核主成分分析（KPCA）方法提取非线性特征时，忽略数据局部结构特征的缺陷，综合核主成分分析全局结构保持和核局部保持投影（KLPP）局部结构保持的优点，提出一种改进核主成分分析方法（MKPCA）。该方法在解决非线性问题的同时，能够全面提取非线性系统中过程数据的全局特征和局部特征，包含更加丰富的特征信息，并将之作为FDA 方法的输入，使用判别矢量的距离进行故障检测，根据最优特征矢量间的相似度系数来快速识别故障，充分利用了MKPCA 方法特征提取能力和FDA 方法监督学习能力，实现两种方法的优势结合。采用Tennessee Eastman 过程故障检测数据集进行仿真实验，表明了本文所提方法在故障检测与诊断中的优势。

[1]Zhou Donghua (周东华),Li Gang (李钢),Li Yuan (李元).Data Driven Industrial Process Fault Diagnosis Technology Based on Principal Component Analysis and Partial Least Squares (数据驱动的工业过程故障诊断技术:基于主成分分析与偏最小二乘的方法) [M].Beijing:Science Press,2011:1-9.

[2]Yin S,Ding S X,Haghani A,et al.A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process [J].Journal of Process Control,2012,22 (9):1567-1581.

[3]Alcala C F,Joe Qin S.Analysis and generalization of fault diagnosis methods for process monitoring [J].Journal of Process Control,2011,21 (3):322-330.

[4]Zhang M,Ge Z,Song Z,et al.Global-local structure analysis model and its application for fault detection and identification [J].Ⅰndustrial & Engineering Chemistry Research,2011,50 (11):6837-6848.

[5]Garcia-Alvarez D,Fuente M J,Sainz G I.Fault detection and isolation in transient states using principal component analysis [J].Journal of Process Control,2012,22 (3):551-563.

[6]Xu Yuan (徐圆),Liu Ying (刘莹),Zhu Qunxiong (朱群雄).A complex process fault prognosis approach based on multivariate delayed sequences [J].CⅠESC Journal(化工学报),2013,64 (12):4290-4295.

[7]Han Min (韩敏),Wang Yanan (王亚楠).Prediction of multivariate time series based on reservoir principal component analysis [J].Control and Decision(控制与决策),2009,24 (10):1526-1530.

[8]Lei Meng (雷萌),Li Ming (李明).NIRS prediction model of calorific value of coal with KPCA feature extract [J].CⅠESC Journal(化工学报),2012,64 (12):3991-3995.

[9]Song Bing (宋冰),Ma Yuxin (马玉鑫),Fang Yongfeng (方永锋),et al.Fault detection for chemical process based on LSNPE method [J].CⅠESC Journal(化工学报),2014,65 (2):620-627.

[10]Tong C,Yan X.Statistical process monitoring based on a multi-manifold projection algorithm [J].Chemometrics and Ⅰntelligent Laboratory Systems,2014,130:20-28.

[11]Zhang Ni (张妮),Tian Xuemin (田学民),Cai Lianfang (蔡连芳).Nonlinear process fault detection method based on RISOMAP [J].CⅠESC Journal(化工学报),2013,64 (6):2125-2130.

[12]Sprekeler H.On the relation of slow feature analysis and laplacian eigenmaps [J].Neural Computation,2011,23 (12):3287-3302.

[13]Ma Yuxin (马玉鑫),Wang Mengling (王梦灵),Shi Hongbo (侍洪波).Faule detection for chemical process based on locally linear embedding [J].CⅠESC Journal(化工学报),2012,63 (7):2121-2127.

[14]Wong W K,Zhao H T.Supervised optimal locality multi-manifold projection algorithm [J].Chemometrics and Ⅰntelligent Laboratory Systems,2014,130:20-28.

[15]Deng X,Tian X.Sparse kernel locality preserving projection and its application in nonlinear process fault detection [J].Chinese Journal of Chemical Engineering,2013,21 (2):163-170.

[16]Yu J.Local and global principal component analysis for process monitoring [J].Journal of Process Control,2012,22 (7):1358-1373.

[17]Luo L,Bao S,Gao Z,et al.Batch process monitoring with tensor global-local structure analysis [J].Ⅰndustrial & Engineering Chemistry Research,2013,52 (50):18031-18042.

[18]Alcala C F,Qin S J.Reconstruction-based contribution for process monitoring [J].Automatica,2009,45 (7):1593-1600.

[19]He Q P,Qin S J,Wang J.A new fault diagnosis method using fault directions in fisher discriminant analysis [J].AⅠChE Journal,2005,51 (2):555-571.

[20]Zhang X,Ma S,Yan W W,et al.A novel systematic method of quality monitoring and prediction based on FDA and kernel regression [J].Chinese Journal of Chemical Engineering,2009,17 (3):427-436.

[21]Fan J,Qin S J,Wang Y.Online monitoring of nonlinear multivariate industrial processes using filtering KICA-PCA [J].Control Engineering Practice,2014,22:205-216.

[22]Martin E B,Morris A J.Non-parametric confidence bounds for process performance monitoring charts [J].Journal of Process Control,1996,6 (6):349-358.