丁烯醛及丁烯醛-乙醛二元体系汽液相平衡模拟

杨华明，张敏华，马静

（1 天津大学石油化工技术开发中心，绿色合成与转化教育部重点实验室，天津 300072； 2 天津化学化工协同创新中心，天津 300072）

引 言

丁烯醛又名巴豆醛，是一种无色、易燃，具有催泪性，在水中溶解度适中，在有机溶剂中易溶的醛类物质[1]。其工业应用广泛，常用于食品防腐剂、酵母和霉菌抑制剂山梨酸的制备，也可用作酒精抑制剂和四乙基铅的稳定剂等[2]。我国现有的乙烯氧化法生产乙醛[3]装置主要采用的德国弗里德里希·伍德有限公司设备[4]，在生产乙醛的同时副产丁烯醛。因此，有效地把副产品丁烯醛从乙醛中进行回收利用是提高工厂经济效益的有效途径，同时可以获得高质量要求的乙醛产品。

流体的汽液相平衡数据是分离技术以及分离设备开发和设计的理论基础。因不受实验条件、体系稳定性等限制，分子模拟法[5-7]成为实验测定方法外又一重要的相平衡数据获取途径。同时，其还具有计算周期短、计算成本低等优势。Gibbs 系综Monte Carlo 法[8-10]（GEMC）因不考虑相边界条件，无须计算化学势，被广泛地应用于流体相平衡的计算中。Gibbs 系综Monte Carlo 法计算汽液相平衡数据的准确性直接与力场相关。常见的力场有TraPPE力场[11-12]、OPLS 力场[13]、AUA 力场[14]等。

其中，美国明尼苏达大学Siepmann 课题组开发的TraPPE 力场参数是通过拟合液相及临界点实验数据所得，因此在汽液相平衡计算方面较为准确。同时，联合原子力场（UA）的计算速率要高于全原子力场（AA）的计算速率。Siepmann 课题组已经分别对正构烷烃[8]，直链和支链烯烃[11]，醚、酮、醛类[12]等体系进行了系统性研究，并补充了相关基团的非键作用参数及键参数，将该力场应用于相关物质纯组分及混合组分的汽液相平衡计算中，取得了相当高的准确度。然而，TraPPE 力场中关于烯醛类的参数还不完善，如缺少烯醛类物质的键长和二面角扭转项参数。本文以TraPPE-UA 力场为基础，采用基于第一性原理的量子化学方法对缺少的键长参数和二面角扭转项参数进行了计算，补充了丁烯醛中缺失的力场参数。采用构建的力场参数计算了丁烯醛纯组分、丁烯醛与乙醛二元体系的汽液相平衡数据，并将计算结果与实验数据进行了比较，以期为化工分离过程提供基础数据。

1 力场模型

TraPPE-UA 为TraPPE 联合原子力场，即将CHx（0≤x≤4）基团作为一拟原子，作用中心在C 原子上。键相互作用参数[11-12]中，键长采用固定键长形式（表1）。

表1 TraPPE-UA 力场中丁烯醛及乙醛键参数Table 1 Bond parameters of crotonaldehyde and ethanal in TraPPE-UA force field

被两原子键分开的三原子间通过谐波弯曲势能相互作用

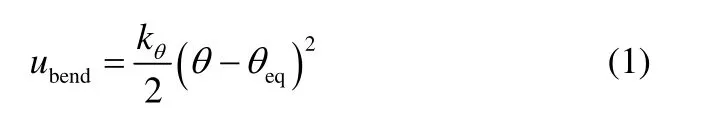
式中，kθ、θ、θeq分别为力常数、键角以及平衡键角（表2）。

被三原子键分开的四原子间通过余弦形式的扭转势能交互作用

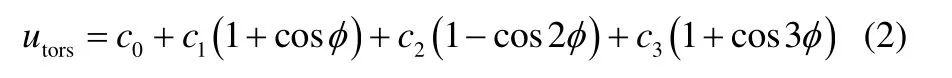
式中，φ和ci分别为扭转角和系数项。而中间键为双键的反式结构，采用固定二面角，d为固定二面角扭转项参数（表3）。

表2 TraPPE-UA 力场中丁烯醛及乙醛弯曲项参数Table 2 Bend parameters of crotonaldehyde and ethanal in TraPPE-UA force field

表3 TraPPE-UA 力场中丁烯醛及乙醛扭转项参数Table 3 Torsion parameter of crotonaldehyde and ethanal in TraPPE-UA force field

非键交互作用是由Lennard-Jones（LJ）作用和库仑势能组成

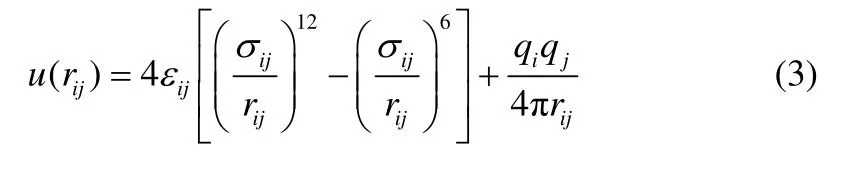
式中，rij、εij、σij、qi和qj分别为原子间距、LJ阱深参数、LJ 半径，以及原子i和j的局部电荷（表4）。本计算过程中，LJ 参数通过迁移TraPPE 力场参数[11-12]获得，电荷进行自动分配。

表4 TraPPE-UA 力场中丁烯醛及乙醛非键相互作用参数Table 4 TraPPE-UA force field parameters for nonbonded interactions of crotonaldehyde and ethanal

分子间相互作用通过Lorentz-Berthelot（LB）混合规则进行计算

2 计算细节

2.1 键长及扭转项参数计算

2.2 GEMC 计算

计算使用MCCCS Towhee[17]软件，采用补充后的TraPPE-UA 力场参数对丁烯醛纯物质、丁烯醛与乙醛二元体系进行了GEMC 计算。丁烯醛纯组分计算使用500 个分子，丁烯醛与乙醛混合物计算共使用500 个分子。计算首先进行2000000 步MC 运动进行预平衡，之后进行3000000 步MC 运动进行平衡。通过比较预平衡中的块平均密度，2000000 步足够使体系趋于平衡状态。模拟过程中，体积变化概率、粒子交换概率、分子再生长概率、平动和转动概率分别为0.2%、15.8%、28%、28%和28%。对于二元组分的计算，初始体积及分子数的设定值需要同最终平衡值进行比较，并保证它们之间的差值不大[18]。

3 结果与讨论

3.1 键参数

分别采用B3LYP 和MP2 方法对丁烯醛分子进行结构优化（图1），其键长值见表5。两种方法所得键长参数相差0.0001 nm，与实验值[1]相比相差0.0002 nm。本文选用0.1469 nm 作为TraPPE-UA 力场中丁烯醛缺少的CH CH 键参数，进行GEMC计算。

图1 丁烯醛优化后结构Fig.1 Optimizational structure of crotonaldehyde

表5 TraPPE-UA 力场中CH CH 键长参数Table 5 Bond parameter of CH CH in TraPPE-UA force field

对CH CH CH O 二面角进行扭转并分别采用B3LYP 和MP2 方法计算新构型能量，将计算所得扭转能代入式(2)进行拟合获得扭转项参数。拟合结果如图2、表6所示。

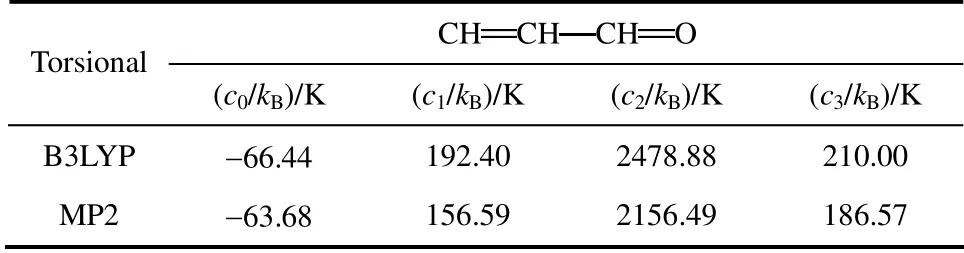
表6 TraPPE-UA 力场中CH CH CH O 二面角扭转项参数Table 6 Torsional parameters of CH CH CH O in TraPPE-UA force field

图2中采用B3LYP 和MP2 方法获得的扭转能曲线与拟合曲线吻合度较高，相关系数分别为99.862%和99.897%。本文选用拟合度稍高的MP2方法计算获得的二面角参数作为TraPPE-UA 力场中丁烯醛缺少的CH CH CH O 二面角参数，进 行GEMC 计算。

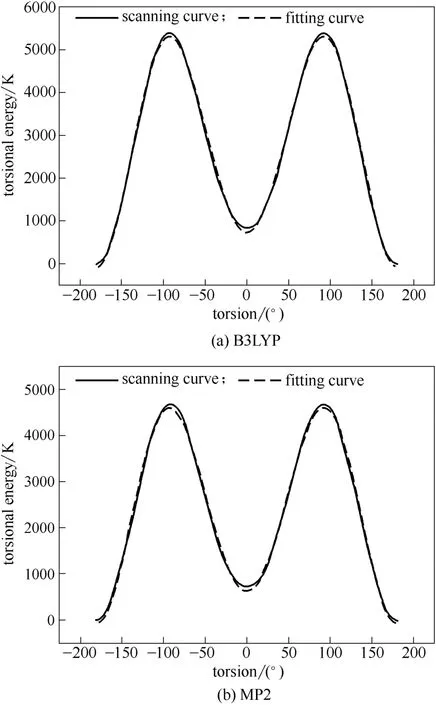
图2 丁烯醛分子中CHCHCHO 二面角 扭转能拟合曲线Fig.2 Torsional energies and fitting curves of CHCHCHO in crotonaldehyde

3.2 丁烯醛纯组分汽液相平衡模拟

本文采用TraPPE-UA 力场，并采用新补充的键长和扭转项参数进行丁烯醛纯组分汽液相平衡模拟。临界温度和临界密度通过式(5)、式(6)[19-20]计算得到

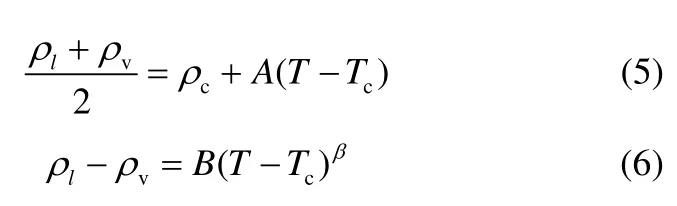
式中，ρl、ρv、ρc分别为液相、气相和临界密度，T、Tc分别为对应温度和临界温度，A、B为可调参数，β为临界指数，一般设定为0.32。并将结果与实验值进行比较。计算结果如图3、表7所示。

从图3、表7中可以看出，丁烯醛液相密度的模拟结果与实验数据[21]相比，其误差最低为0.28%，最高为1.23%。产生误差的原因有：丁烯醛体系含有顺式丁烯醛、反式丁烯醛两种构型，其中反式丁烯醛含量高达95%以上，模拟过程中对此做近似处理；量子化学计算过程中，选用的方法本身存在微小误差。临界温度模拟结果为562.77 K，与实验值571.15 K 相比误差为1.46%，临界密度模拟值为288.23 kg·m-3，与实验值280.36 kg·m-3相比误差为2.81%。通过将模拟值与实验值比较发现，采用TraPPE-UA 力场计算的汽液相平衡数据具有较高的准确性。

图3 丁烯醛纯组分汽液相平衡数据Fig.3 Vapor-liquid equilibria data of pure crotonaldehyde

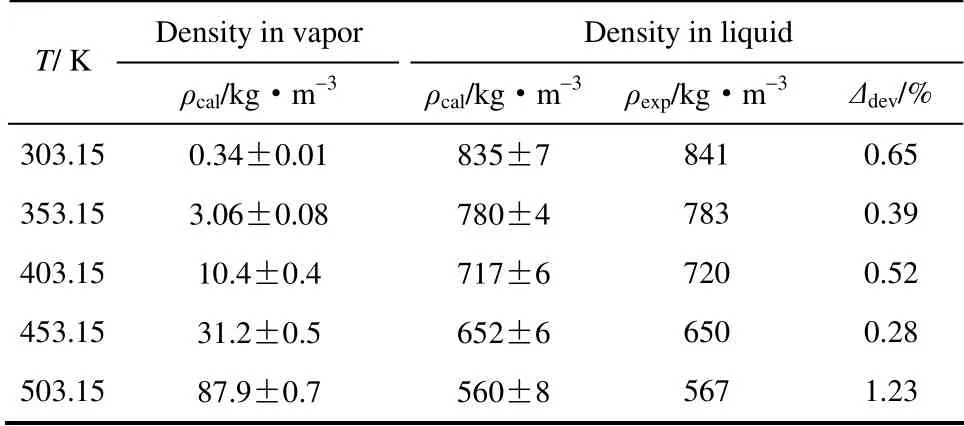
表7 采用TraPPE-UA 力场计算的丁烯醛纯组分 汽液相平衡数据Table 7 Vapor-liquid equilibria data of pure crotonaldehyde calculated by TraPPE-UA force field

3.3 丁烯醛、乙醛二元体系的汽液相平衡模拟

本文采用TraPPE-UA 力场，并采用新补充的键长和扭转项参数对丁烯醛、乙醛二元体系的汽液相平衡进行了计算，压力条件为101325 Pa，并将模拟结果与实验值[3]进行比较。实验数据是在101325 Pa条件下，通过Rose 釜测量所得，经过活度系数方程验证，平均误差最高为0.56%，计算结果如图4、表8所示。

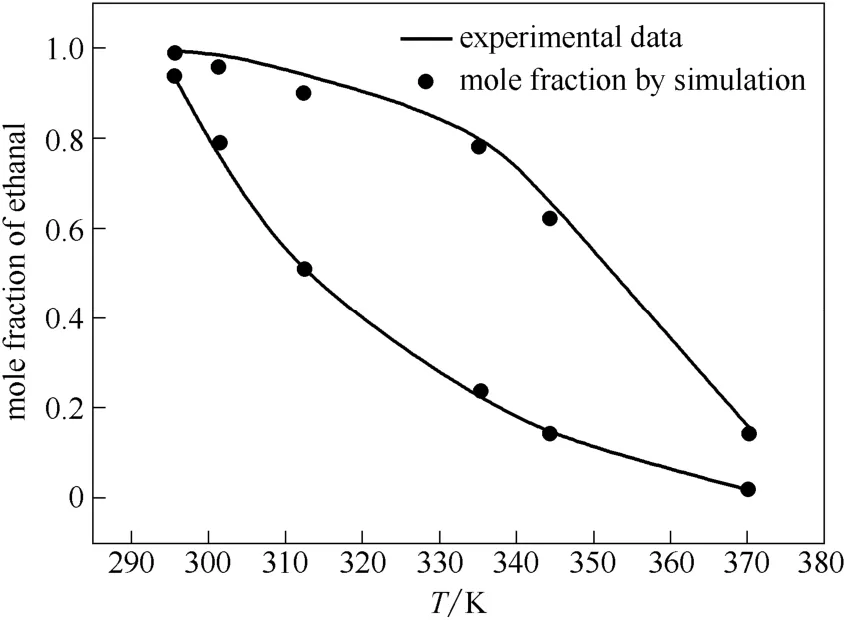
图4 丁烯醛与乙醛组分汽液相平衡数据Fig.4 Vapor-liquid equilibria data of crotonaldehyde and ethanal mixture

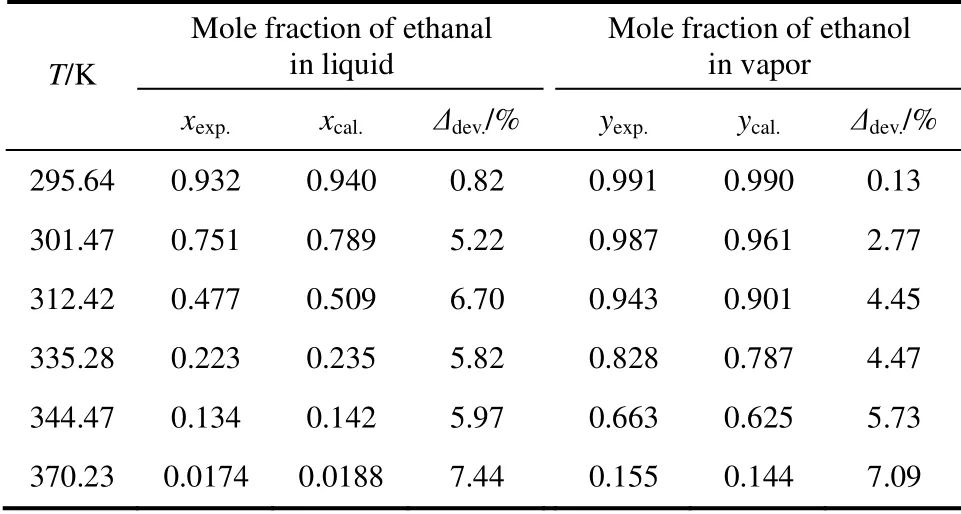
表8 采用TraPPE-UA 力场计算的丁烯醛与乙醛二元体系汽液相平衡数据Table 8 Vapor-liquid equilibria data of crotonaldehyde and ethanal mixture calculated by TraPPE-UA force field

从图4、表8中可以看出，丁烯醛与乙醛二元体系的汽液相平衡数据的模拟结果与实验值相比，液相误差范围为0.82%～7.44%，气相误差范围为 0.13%～7.09%。相比于丁烯醛纯组分，丁烯醛与乙醛二元体系模拟结果的准确性略差，这与二元体系的相互作用相比于纯组分更为复杂有关，需要更准确的力场参数对其进行描述。

4 结 论

本文采用基于第一性原理的量子化学方法，对丁烯醛在TraPPE-UA 力场缺失的键参数和二面角扭转项参数进行了计算，完善了丁烯醛分子的TraPPE-UA力场参数。采用GEMC 方法，对丁烯醛纯组分、丁烯醛与乙醛二元体系进行了汽液相平衡计算，并与实验数据进行了对比。模拟结果显示了较高的准确性。对于丁烯醛与乙醛二元混合体系，基于二元体系相互作用的复杂性，模拟结果的准确性要低于纯组分。在今后的研究中，还需要更准确的力场参数来对其进行描述，其普遍性也有待进一步的验证。

符 号 说 明

A，B——参数

ci——二面角扭转项公式系数，J

d——固定二面角扭转项参数，K

kθ——键角弯曲力常数，J

r——键长，nm

rij——原子间距，nm

T——温度，K

ubend——谐波弯曲势能，K

u(rij)——非键相互作用能，K

utors——扭转势能，K

x——液相摩尔分数

y——气相摩尔分数

β——临界指数

Δdev——误差值，%

εij——LJ 阱深参数，J

θ——键角弯曲度，（°）

θeq——平衡键角，（°）

ρ——密度，kg·m-3

σij——LJ 半径，nm

ϕ——二面角角度，rad

下角标

bend——键角

cal.——模拟计算值

dev——误差

eq——平衡态

exp.——实验值

i，j——组分i，j

tors——二面角

[1]Jayaprakash A,Arjunan V,Jose S P,Mohan S.Vibrational and electronic investigations,thermodynamic parameters,HOMO and LUMO analysis on crotonaldehyde byab initioand DFT methods [J].Spectrochimica Acta Part A:Molecular and Biomolecular Spectroscopy,2011,83:411-419

[2]Fernandez J E,Solomons T W G.Crotonaldehyde [J].Chem.Rev.,1962,62:485-502

[3]Shanghai Wusong Chemical Plant (上海吴淞化工厂),Department of Chemical Engineering,Zhejiang University (浙江大学化工系).Vapor-liquid equilibria in ethanol-crotonaldehyde-water ternary system [J].Chemical Engineering(China)（化学工程），1976 (6):1-31

[4]Fan Wenge (范文革),Zhang Deguang (张德光),Hu Jiwei (胡继伟).Discussion on way out for China’s existing acetaldehyde production plants using ethylene oxidation process [J].Refining and Chemical Industry(炼油与化工),2007,18 (1):8-9

[5]Li Xiaofeng,Zhao Lifeng,Cheng Tao,Liu Lianchi,Sun Huai.One force field for predicting multiple thermodynamic properties of liquid and vapor ethylene oxide [J].Fluid Phase Equilb.,2008,274 (1/2):36-43

[6]Xu W H,Yang J C.Computer simulations on aggregation of acetic acid in the gas phase,liquid phase,and supercritical carbon dioxide [J].J.Phys.Chem.A,2010,114:5377-5388

[7]Shi Xiaoming (施晓明).Vapor-liquid equilibria simulation by GEMC [D].Chongqing:Chongqing University,2006

[8]Martin M G,Siepmann J I.Transferable potentials for phase equilibria (Ⅰ):United-atom description ofn-alkanes [J].Journal of Physical Chemistry B,1998,102 (14):2569-2577

[9]Panagiotopoulos A Z.Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble [J].Molecular Physics,1987,61 (4):813-826

[10]Panagiotopoulos A Z,Quirke N,Stapleton M,Tildesley D J.Phase equilibria by simulation in the Gibbs ensemble:alternative derivation,generalization and application to mixture and membrane equilibria [J].Molecular Physics,1988,63 (4):527-545

[11]Wick C D,Martin M G,Siepmann J I.Transferable potentials for phase equilibria (Ⅳ):United-atom description of linear and branched alkenes and alkylbenzenes [J].J.Phys.Chem.B,1998,102 (38):2569-2577

[12]Stubbs J M,Potoff J J,Siepmann J I.Transferable potentials for phase equilibria (Ⅵ):United-atom description for ethers,glycols,ketones and aldehydes [J].J.Phys.Chem.B,2004,108:17596-17605

[13]Jorgensen W L,Maxwell D S,Tirado-Rives J.Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids [J].J.Am.Chem.Soc.,1996,118 (45):11225-11236

[14]Ungerer P,Nieto-Draghi C,Rousseau B.Molecule simulation of the thermophysical properties of fluids:from understanding toward quantitative predictions [J].J.Mol.Liq.,2007,134:71-89

[15]Becke A D.Density functional thermochemistry (Ⅲ):The role of exact exchange [J].J.Chem.Phys.,1993,98:5648-5652

[16]Stephens P J,Devlin F J,Chabalowski C F,Frisch M J.Ab initiocalculation of vibration absorption and circular dichroism spectra using density functional force fields [J].J.Phys.Chem.,1994,98 (45):11623-11627

[17]Martin M G.MCCCS Towhee:a tool for Monte Carlo molecular simulation [J].Molecular Simulation,2013,39 (14/15):1212-1222

[18]McKnight T J,Vlugt T J H,Ramjugernath D,Starzak M,Ahlström P,Bolton K.Simulation of 1-alkene and alkane binary vapour-liquid equilibrium using different united-atom transferable force fields [J].Fluid Phase Equilibria,2005,232 (1/2):136-148

[19]Rowildson J S,Widom B.Molecular Theory of Capillarity [M].New York:Oxford University Press,1989:261

[20]Rowildson J S,Widom B.Liquids and Liquid Mixtures [M].3rd ed.London:Butterworth,1982:70-75

[21]Yaws C L.Chemical Properties Handbook [M].New York:McGraw-Hill,1999