基于有限元法的钢筋混凝土结构损伤识别

马钊++强宇明

摘 要：结构损伤识别方法是桥梁结构健康监测系统的重要组成部分，也是目前国际上工程界研究的热点问题，具有很强的工程背景和重要的实用价值。基于此，提出了一种基于可降阶有限元模型与自适应均方误差的损伤检测方法对线性结构和非线性结构进行损伤识别，同时通过试验数据来验证该方法对结构损伤预测的有效性。试验结果说明，该方法能有效识别钢筋混凝土结构的时变非线性参数，包括刚度，强度衰减量及结构的箍缩效应，给工程实践提供重要参考价值。

关键词：有限元模型；损伤识别；强度衰减；捻缩效应

中图分类号：U441.4 文献标志码：A 文章编号：1672-1098（2015）02-0053-07

The Structural Damage Identification Technology Based on the

Finite Element Method for Reinforced Concrete

MA Zhao， QIANG Yu-ming

（Shaanxi Open University， Xi'an Shaanxi 710119， China）

Abstract：Structural damage identification is the important aspect of the bridge structural health monitoring system； it is also a hot topic in international engineering field at present and it has very important engineering background and practice value. Based on this， it was proposed that a combination of the reduced-order finite-element model and the adaptive quadratic sum-square error with unknown inputs method identifies the damage of linear and nonlinear structure， and the experimental data of the test is used to illustrate the performance of the proposed damage identification method. The experimental results showed that the proposed damage identification method is capable of identifying time-varying nonlinear parameters， including stiffness and strength degradations as well as the pinching effect， which provides an important value for engineering practice.

Key words：finite-element model； damage identification； strength degradation； pinching effect

在结构的服役过程中，由于环境载荷、材料老化、疲劳效应、腐蚀效应等导致结构损伤迅速扩展，使得整个结构毁坏，造成突发性灾难事故，因此，研究结构的早期损伤检测、诊断对结构的安全性具有重要意义[1-2]。关于结构损伤的定量化评价，常采用有限元方程法，而伴随有限元方程引入的大量自由度，使得求解时变结构参数变得非常复杂，同时需要大量的测试传感器。基于此，文献[3-4]提出了一种基于未知输入参数的可降阶有限元方程与自适应均方误差的损伤检测方法来识别线性结构损伤。本文将这种方法应用于非线性钢筋混凝土损伤检测，并利用试验数据来验证该方法的有效性。

选取两种结构模型来模拟该双层钢筋混凝土框架结构的动力学特性，包括：① 一个等效线性时变扭转弹簧系统；② 一个由时变弹性元件和塑性铰组成的非线性模型。采用一种具有强度和刚度退化以及捻缩效应的光滑滞回模型来代替塑性铰的滞回性能，根据未知输入的可降阶有限元模型与自适应均方误差算法，对一个双层钢筋混凝土框架进行振动台试验测试，验证本文提出的损伤检测方法的性能与效率，得出相关的结论。

1 试验系统物理模型及有限元模型

11 物理模型的建立

试验中测试的双层钢筋混凝土框架的整个建筑高度198 m， 层高098 m，平面尺寸为：218 m×15 m，每层重2吨，设计的一阶固有频率为12 Hz，结构的具体尺寸如图1所示。在振动台上施加不同强度的白噪声和集集地震激励，检测结构在不同激励强度下的损伤程度[5]。

在试验中，每层结构和振动台上安装加速度传感器，测量每层的加速度响应1和2以及振动台的加速度0，采样频率为200 Hz，最后根据试验数据进行结构损伤识别及时变参数的识别。

图1 双层钢筋混凝土框架的实体模型12 有限元模型的建立

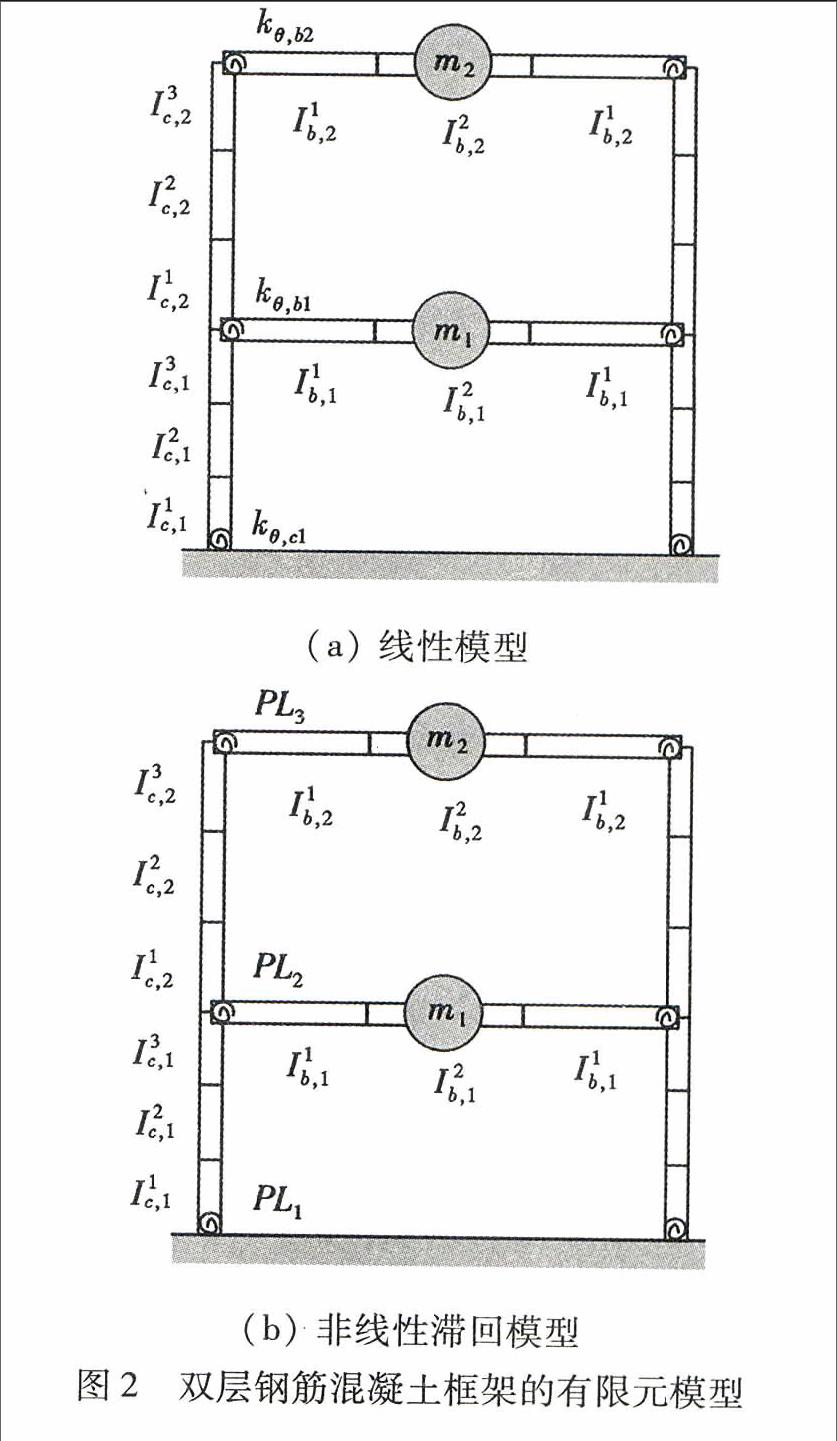
双层钢筋混凝土结构的每个支柱和横梁被分解成三个有限单元，并根据静力凝聚法，每个有限元运动方程被缩聚为两个自由度的降阶系统。首先，将结构缩聚为一个具有时变系统参数的等效线性结构，比如时变刚度，利用损伤检测技术来追踪每个结构有限单元的刚度退化。然后，将结构看成节点单元为塑性铰的非线性结构，每个塑性铰具有光滑滞回特性，并考虑其刚度、强度退化和捻缩效应，对应的有限元模型如图2所示。

根据有限元方程，n自由度复杂非线性结构的运动矢量方程可表示为[6-8]：endprint

（2）

式中：η*为f*（t）的激励影响矩阵；η为f（t）的激励影响矩阵。

13 结构边界条件的处理

在结构分析中，节点一般为铰接或完全刚性连接，因为节点的性能是导致结构垮塌的关键因素。在半刚性连接的多种可能形变模式中，最重要的是因弯曲运动引起的旋转变形。因此，根据有限元模型中连接刚度的降低量可定量检测结构节点的损伤。将2个横梁和4个立柱划分为18个单元，整个系统的刚度矩阵有4个单元组成（柱单元，下端节点有旋转刚度的柱单元，两端节点可旋转的梁单元，两端节点可旋转和平移的梁单元）。

图2a中，Ei，Ii和Li分别为结构中第i个单元的杨氏模量，惯性矩和单元长度。ki是第i个单元的等效刚度，kθi是梁、柱连接处的旋转刚度，αi是旋转刚度因子，因此，节点处的损伤可由旋转刚度kθi的衰减量确定。

（4）

图2b中，用塑性铰代替图2a中的旋转弹簧，双层结构的非线性有限元模型包括18个弹性单元和6个弹性铰。利用退化滞回模型描述塑性铰行为[9]，对于该滞回模型，考虑到捻缩效应，刚度和强度退化，一个塑性铰可用屈服后弹簧（KP）、滞回弹簧（Kh）和滑锁弹簧（Ks）三个弹簧来替代，其中，屈服后弹簧：

KP=αPK

（5）

式中：K弹簧初始刚度；αP弹簧屈服前后刚度比。

滞回弹簧：

（6）

式中：fn滞回弹簧标准强度； f*作用在滞回弹簧和滑锁弹簧上的力；η卸载曲线形状控制参数；Φ， ψ分别定义第i个循环刚度、强度的退化。

滑锁弹簧：

2 基于试验数据的损伤识别

根据一个等效线性时变结构和一个由弹性时变单元和塑性铰组成的非线性结构，建立双层钢筋混凝土模型。利用试验数据和损伤识别技术识别两种模型的未知时变结构参数，具体的试验激励参数如表1所示。

图4 载荷6（a）下加速度响应的识别值与测量值

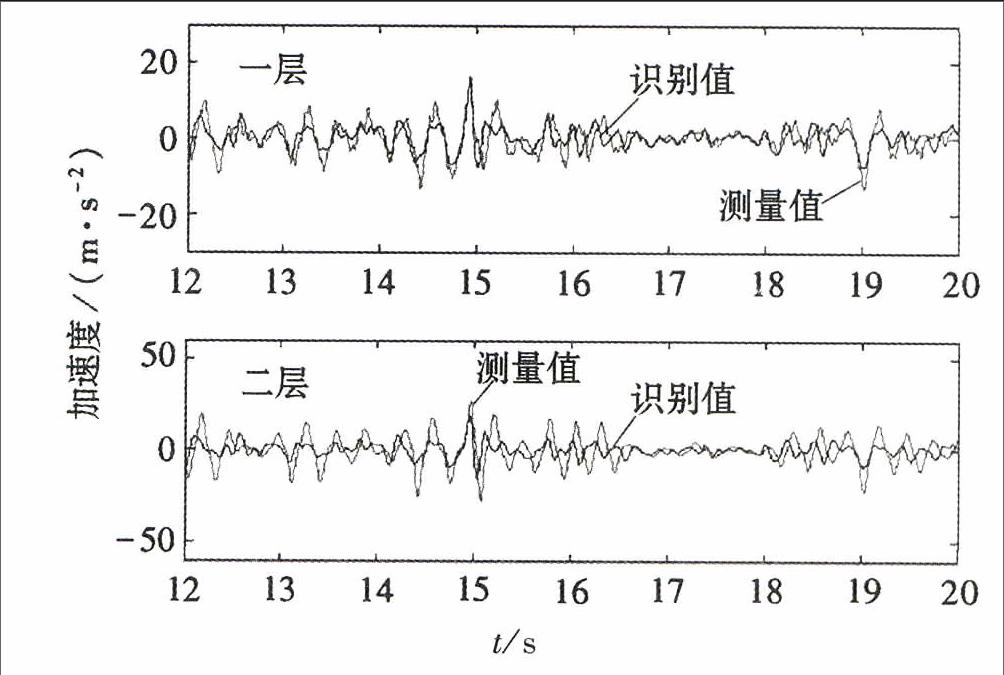
在5（b）和6（a）载荷下，对比响应加速度的预测值与响应加速度的测量值，发现有限元预测值与试验测试值具有很好的一致性。因此，根据提出的输入未知的自适应均方误差算法，通过执行自适应矩阵算法能很好的预测时变参数的改变量。

不同载荷序列下结构参数值的确定如图5～图7所示，在连续加载条件下，随着振动载荷强度的增加，每个结构单元的惯性矩和旋转刚度降低，用每个结构单元的惯性矩衰减量来表示刚度衰减量。

加载强度/（cm·s-2）

1. 惯性矩I1c，1； 2. 惯性矩I2c，1； 3. 惯性矩I3c，1； 4. 惯性矩I1c，2； 5. 惯性矩I2c，2； 6. 惯性矩I3c，2

图7 不同载荷序列下，梁旋转刚度参数的确定

可降阶有限元方程与自适应均方误差法能在输入参数未知的条件下，对未知结构参数值进行确定。因此，现场测试过程中所需的传感器减少，并根据此方法对图1所示的双层钢筋混凝土框架结构在输入参数未知条件下的结构损伤进行了确定。在表1的载荷序列下，根据可降阶有限元方程与未知输入参数下的自适应均方误差法，预测出的未知参数值随载荷的变化如图8～图10所示。将该预测值与测量值进行比较发现，两者非常接近。

刚度kθ，c3

图10 不同载荷序列下柱，梁旋转刚度参数的确定

另外，采用参数识别方法，可计算出未知输入参数和时变参数。在载荷7（a）和8（a）下，结构在地震激励下加速度测量值与识别值随时间变化的关系如图11～图12所示，测量值和通过计算得到的识别值具有很好的一致性，这表明基于可降阶有限元方程与自适应均方误差的损伤检测方法在未知输入条件下都能有效识别结构参数，从而判断结构损伤程度。

图12 载荷8（a）下加速度响应的识别值与测量值22 非线性塑性铰模型的识别

对于非线性模型，线性模型中的旋转刚度被具有滞回特征的塑性铰取代。根据图2的对称性，三个独立的塑性铰分别为PL1， PL2， PL3。 每个塑性铰包含8个未知的滞回模型参数，整个双层结构包括24个未知的滞回模型参数，10个惯性矩参数以及2个阻尼系数参数，θ可表示为

（9）

式中：θ 的前8个元素为第一个塑性铰的未知滞回参数。

根据测得的每层的加速度响应，利用可降阶有限元方程与自适应均方误差法，可确定出36个未知参数值，根据塑性铰刚度和强度的衰减量可判断该双层结构的损伤程度。参数的初始赋值为

不同载荷序列下，线弹性单元未知惯性矩参数的识别值如图13～图14所示，对比图5～图7可以看出，非线性模型的惯性矩参数衰减量小于线性模型的衰减量，这是因为非线性模型的能量通过塑性铰耗散的。

加载强度/（cm·s-2）

1. 惯性矩I1c，1； 2. 惯性矩I2c，1； 3. 惯性矩I3c，1； 4. 惯性矩I1c，2； 5. 惯性矩I2c，2； 6. 惯性矩I3c，2

图13 不同载荷序列下柱体惯性矩参数的确定

图14 不同载荷序列下梁惯性矩参数的确定

另外，计算了3个塑性铰的刚度，在不同载荷序列下，这3个塑性铰的刚度、强度衰减因子值如图15～图16所示。在前5个激励载荷，强度从200 cm/s2到600 cm/s2下，塑性铰刚度、强度的衰减很小，随着激励强度的提高，塑性铰的刚度、强度衰减较为显著。

图15 不同载荷序列下塑性铰的刚度衰减因子

图16 不同载荷序列下塑性铰的强度衰减因子

在8（a）载荷下，各层加速度相应的测量值与识别值对比如图17所示，加速度的识别值和测量值具有很好的一致性。因此，提出的可降阶有限元方程与自适应均方误差法预测能在输入参数未知条件下，给出较为准确的预测值，其对结构的定量损伤评定是可信的、准确的。endprint

图17 载荷8（a）下加速度响应的识别值与测量值

3 结论

1） 利用可降阶有限元方程及自适应均方误差法，建立了试验系统的有限元模型并确定了边界条件，通过试验验证，该模型能够有效预测结构的损伤。

2） 对线性和非线性双层钢筋混凝土结构的时变参数进行了确定，并对钢筋混凝土结构的刚度，强度衰减量及结构的箍缩效应进行了预测，预测结果与试验结果基本吻合，验证了模型的合理性。

3） 通过实验数据对提出的结构损伤识别方法进行验证，验证结果说明该方法能有效的识别出钢筋混凝土结构的时变非线性参数，包括刚度，强度衰减量及结构的箍缩效应，对指导工程实践具有重要的参考价值。

参考文献：

[1] R P BANDARA， TOMMY H T CHAN， D P THAMBIRTNAM.Frequency response function based damage identification using principal component analysis and pattern recognition technique[J]. Engineering Structures， 2014（66）： 116-128.

[2] 朱宏平， 余璟， 张俊兵. 结构损伤动力检测与健康监测研究现状与展望 [J]. 工程力学， 2011， 28（2）： 1-11.

[3] J N YANG， H HUANG， S PAN.Adaptive Quadratic Sum-Squares Error for Structural Damage Identification [J]. ASCE Journal of Engineering Mechanics， 2009， 135（2）： 67-77.

[4] J N YANG， Y XIA， C H LOH.Experimental demonstration of the AQSSE damage detection technique detection technique based on finite-element approach[J]. Proceedings of SPIE， 2010， 7647（76474C）： 1-12.

[5] J H WENG， C H LOH， J N YANG.Experimental study of damage detection by data-driven subspace identification and finite-element model updating[J]. ASCE Journal of Structural Engineering， 2009， 135（12）：

1 533-1 544.

[6] A K CHOPRA.Dynamic of Structures： Theory and Applications to Earthquake Engineering[M]. Prentice-Hall Inc.， New Jersey， 2001， 367-370.

[7] M SHINOZUKA， R GHANEM.Structural System Identification.Ⅱ：Experimental Verification[J].ASCE Journal of Engineering Mechanics，1995， 121（2）：256-273.

[8] A L WU， J N YANG， C H LOH.Detection of damages in nonlinear reinforced concrete frames[C]// Proceeding of 20th SPIE Conference on Sensors and Smart Structures Technologies for Civil， Mechanical and Aerospace Systems， 2011， 7981（79812O）：1-13.

[9] M V SIVASELVAN， A M REINHORN.Hysteretic models for deteriorating inelastic structures[J]. ASCE Journal of Engineering Mechanics， 2000， 126： 633-640.

欢迎订阅《安徽理工大学学报（自然科学版）》，欢迎投稿

《安徽理工大学学报（自然科学版）》1981年创刊，季刊，每期定价5.00元，全年定价20.00元。《安徽理工大学学报（自然科学版）》为安徽理工大学主办的综合性学术刊物，主要刊载地质工程、环境工程、测绘工程、采矿工程、安全工程、信息管理与信息系统、土木工程、建筑学、机械工程、测控技术与仪器、自动化、电子信息工程、计算机科学与技术、矿物加工工程、化学工程与工艺、弹药工程与爆炸技术、制药工程、信息与计算科学、应用物理学、医学以及相关基础学科的学术论文和最新研究成果等。

本刊国内外公开发行，侧重体现本校特色，面向国内外组稿。本刊是《CAJ-CD规范》执行优秀期刊，美国《化学文摘》（CA）源期刊，美国《剑桥科学文摘》（CSA）源期刊，俄罗斯《文摘杂志》（VINITI）源期刊，《中国科技论文统计》源期刊，《中文科技期刊数据库》源期刊，《中国学术期刊综合评价数据库》源期刊，此外，我刊还是《中国期刊网》、《中国学术期刊（光盘版）》全文收录期刊和《万方数据——数字化期刊群》上网期刊。另外，我刊和全国各高校学报、科研院所出版的刊物均有学术交流，凡被本刊发表的研究成果及论文，能很快地传播并及时为国内外同行专家引用。

本刊参加全国非邮发报刊联合征订，请读者向天津市大寺泉集北里别墅17号（邮编300385）天津市河西区联合征订服务部直接汇款订阅，不必先索取订单，由本刊负责将刊物寄给订户。也可直接向本刊订阅，由邮局汇款到安徽省淮南市安徽理工大学学术出版中心endprint