“波纹”内壁搅拌槽内的湍流流动特性

张翠勋，杨锋苓，连继咏

（1山东天力干燥股份有限公司，山东 济南 250014；2山东大学机械工程学院，山东 济南250061；3高效洁净机械制造教育部重点实验室（山东大学），山东 济南 250061；4大众报业集团，山东 济南 250014）

提高混合效率是搅拌领域的一个研究热点。有关搅拌混合的研究始于20世纪50年代[1]，历经约三十年的发展以后，Aref[2]和Ottino[3]提出了混沌混合理论，并对二维混合体系进行了系统研究后得以证明其优越性。随后，将其应用范围由二维拓展到三维，提出了搅拌混沌混合方式[4-5]，为搅拌研究的一个重要里程碑，迄今为止，仍是研究的热点[6]。

纵观搅拌混合的研究可以发现，人们在探索如何提高混合效率时，重点在于优化搅拌桨，而关于搅拌槽的改进则很少。具体来讲，提高搅拌混合效率的主要方式有以下几个方面：一是对搅拌桨的尺寸（例如直径、桨叶厚度）、安装高度等进行优化；二是开发新型搅拌桨，以用于不同的工业搅拌体系，例如Smith[7]设计了一种正反转搅拌桨、Bakker等[8]设计了具有非对称结构的Scaba桨、刘作华等[9]设计了刚柔组合搅拌桨等；三是对搅拌桨的安装方式和运转形式进行改进，主要指空间混沌混合方式，例如偏心搅拌[10]、侧入式搅拌[11]、往复式搅拌[12]、错位搅拌[13]等；四是打破常规的稳态搅拌方式，使搅拌桨以正反转、变速旋转[14]，即所谓的时间混沌混合方式，通过破坏流体流动的周期性，在流体内部诱发混沌，实现流体的高效混合。现有关于搅拌槽结构的改进研究，集中于两个方面：一是研究不同搅拌体系对搅拌槽底部形状的需求，例如固液悬浮体系要求槽底最好是椭圆形，从而利于保证搅拌槽底部与壁面结合处固体颗粒的离底悬浮，而气液混合时对槽底形状则无要求[15]；二是挡板结构形式的改进和优化，现有研究发现，所谓“标准挡板”并非适用于所有搅拌工况，挡板后方还存在“混合死区”，某些情况下，非标准挡板更具有优越性[16-19]。

研究发现，对流体速度场的哪怕是微小的扰动也能产生混沌，提高混合性能[20]。受混沌混合原理的启发，本文中对传统搅拌槽的光滑内壁结构进行了改进，设计了一种“波纹”内壁搅拌槽，通过半圆管对流体的扰动在槽壁附近诱发混沌，以期消除挡板后方的“混合死区”，增强流体的流动与混合性能。

1 搅拌槽结构

图1 搅拌槽结构示意图

本文研究的搅拌体系与文献[21]和文献[22]一致，以便与其结果进行对比。搅拌槽为平底圆柱形有机玻璃槽，直径T=270mm，安装4块挡板，宽度B=T/10。“波纹”壁面通过在搅拌槽内壁上安装半圆管获得，布置方式如图1所示。半圆管的半径为T/20，挡板两侧的半圆管偏离水平方向8°，其余 相邻半圆管之间的偏角为15°。槽内流体为水，密度ρ=1×103kg/m3，黏度μ=1×10-3Pa·s，液位高度H=T。搅拌桨为标准Rushton桨，直径D=93mm，离槽底距离C=H/3，桨叶长度l=D/4，宽度w=D/5，桨叶厚度t=0.02D。搅拌桨的转速N=200r/min，对应的桨叶端部速度为utip=0.974m/s，雷诺数Re=28830。

2 数值模拟

采用标准kε-模型模拟流体的湍流流动特性，该模型对搅拌槽内时均速度的模拟精度较好，且计算量小[22-23]。利用前处理软件Gambit®2.3进行建模，整个求解域分为包含搅拌桨的转子和包含槽内其他静止部分的静子两个区域，分别采用四面体和六面体单元进行离散，共划分了约100万个节点。不同区域的网格尺度不同，最小网格尺度为1mm，约为整个搅拌系统最小尺寸（叶片厚度）的1/2。首先进行稳态求解，搅拌桨与挡板之间的相对运动采用多重参考系法进行模拟，近壁区采用标准壁面函数，动量、湍动能及湍动能耗散率均采用二阶迎风格式进行离散，压力速度耦合采用SIMPLE算法，所有变量的收敛残差均为1×10-4。待收敛后，再以稳态流场计算结果作为初始值进行非稳态计算，时间步长取为1.0×10-3s。模拟时搅拌槽顶部液面假设为平面，搅拌槽、搅拌轴及搅拌桨表面为无滑移壁面，转子以与搅拌桨相同的转速一起旋转，静子保持静止，两者交界面设为界面边界（interface）条件。

3 结果与讨论

3.1 模拟方法验证

为验证数值模型和模拟方法的可靠性，首先将标准配置时的流场模拟结果与文献[21]的实验结果及文献[22]的数值结果进行对比，然后再研究“波纹”内壁搅拌槽内的流场。搅拌流场中桨叶区域内流体的流动最复杂，对该区域内流场的模拟结果可以很好地反映数值模型和模拟方法的有效性。为此，对相邻两挡板中间平面内（θ=45°）径向位置2r/D=1.07处、位于2z/w=-2.5～2.5高度范围内流体的时均速度分布情况进行了研究，结果如图2所示。

可以看出，模拟结果与LDV实验及文献结果吻合较好，再现了标准Rushton桨的径向排出流特征。对于轴向速度，模拟误差最大，标准-kε模型的模拟结果稍大于实验值；径向和切向速度的模拟精度高一些，这两者均以搅拌桨所在高度2z/w=0为中心呈近似对称分布。对比可知，本文所建数值模型和模拟方法是可靠的，可用于搅拌流场的研究。

3.2 流场结构对比

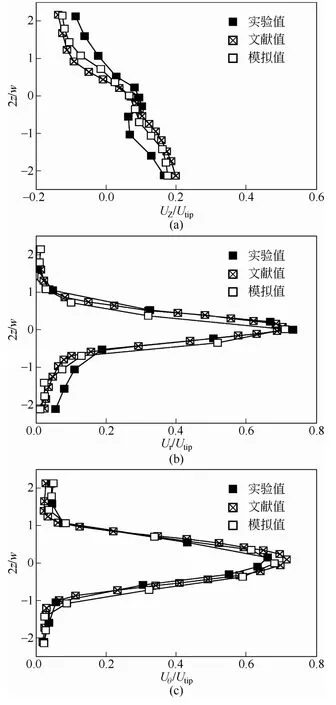
图2 桨叶区域内时均速度的轴向分布

图3 搅拌槽内的速度矢量图

图3和图4分别为搅拌槽内的速度矢量图和速度云图，反映了“波纹”内壁对搅拌槽内流场的影响。 由图3可以看出，搅拌槽内壁结构形式对槽内流体的主循环特征没有显著影响，均呈现典型的双循环流动特征。但搅拌桨所在平面内的速度矢量图表明，不同内壁结构时的流场结构不同：光滑内壁时，挡板后方区域内流体的速度低；改为“波纹”内壁后，半圆管起到扰流的作用，挡板后方区域内流体的速度明显增大，而且整个搅拌桨所在平面内流体的速度分布更为均匀。

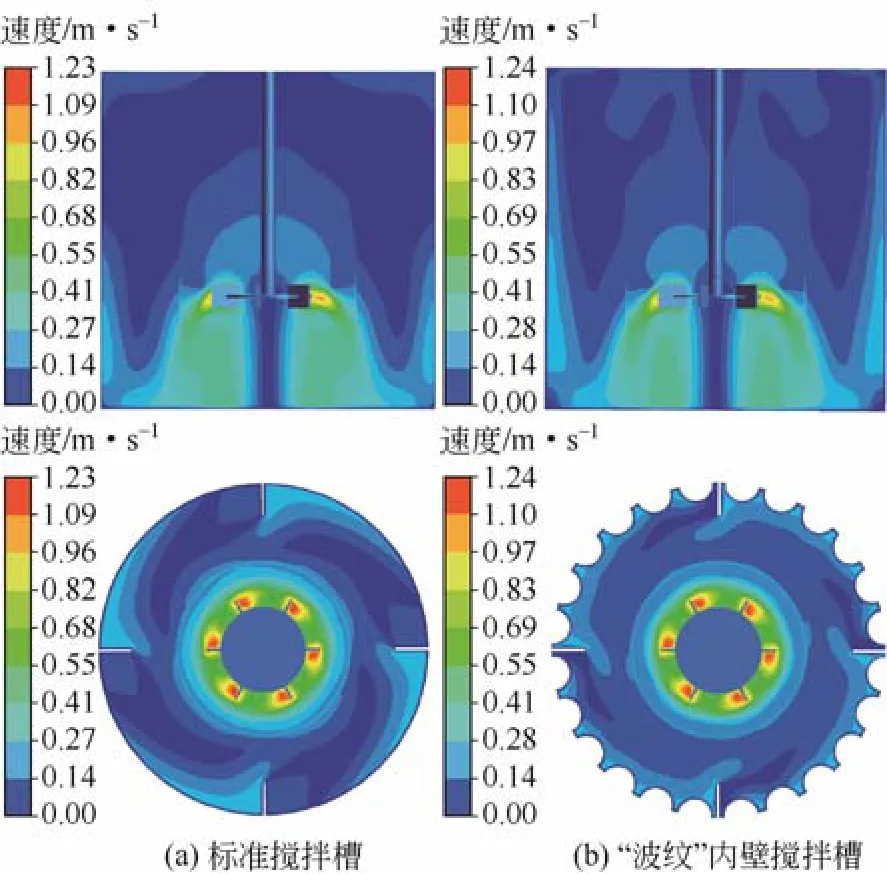
图4 搅拌槽内的速度云图

图4所示的搅拌槽内的速度云图也表明了这一特点。与光滑内壁搅拌槽相比，“波纹”内壁搅拌槽内壁面附近流体的速度明显增大，挡板后方流体的低速区大幅度减少，不过搅拌桨周围流体的速度并 没有变化，表明半圆管主要对壁面周围的流体有扰流作用。另外，从相邻两挡板中间平面内的速度云图可以看出，尽管搅拌桨下方区域内流体的速度没有明显变化，但“波纹”内壁搅拌槽内壁面附近流体的速度得到了提升，而且槽顶部区域内流体的低速区也大幅度减少，这对于改善搅拌槽内流体速度分布的均匀程度起到了很大作用。

3.3 优化

图5 搅拌槽内半圆管的布置示意图

表1 半圆管的安装位置

第3.2节研究证明了“波纹”内壁搅拌槽的优越性，本节中分析半圆管尺寸、数量和安装位置对搅拌流场的影响，其中半圆管数量和安装位置如图5所示。在选择半圆管尺寸时，参考了标准搅拌槽内挡板的尺寸，一般地，B=T/10，因此分别取了R为T/10、T/20T、T/40和T/60共4个不同的半圆管半 径，对应于B、B/2、B/4和B/6，依次记为WSV1、WSV2、WSV3和WSV4。将挡板两侧的半圆管偏离水平方向的角度记为α，其余相邻半圆管之间的夹角记为β，4种不同尺寸时半圆管的角度位置见表1。需要说明的是，受空间的限制，不同配置时布置的半圆管的数量不同，每种配置都以半圆管近似“布满”整个搅拌槽壁为原则。

3.3.1 半圆管尺寸的影响

图6为半圆管半径依次为T/10、T/20、T/40和T/60时搅拌桨所在高度平面内的速度矢量图和速度云图，反映了半圆管尺寸对流场的影响。可以看出，半圆管尺寸对流型无影响，但不同半径的半圆管对流体的扰动程度不同：尺寸越大，即R=T/10时效果最明显，挡板后方的低速区面积显著最小，整个区域内流体的速度分布更加均匀；R=T/20时，半圆管对流体的扰动程度略有降低，挡板后方存在少量低速区；相比之下，R=T/40和T/60时的流场之间没有明显差异，流动性能最差，挡板后方存在明显的低速区。该结果表明，半径越大时，半圆管对流体的扰动程度越强。然而需要注意的是，由于半圆管占据了原本是流体所占据的体积，因此半圆管尺寸越大，流体的有效混合体积就越小。综合考虑半圆管对流体的扰动程度和对流体有效混合体积的削弱程度，确定R=T/20为有效尺寸。

图6 不同半圆管尺寸时搅拌桨所在高度平面内的速度矢量图和速度云图

3.3.2 半圆管数量和位置的影响

图7为相邻两挡板中间平面内的速度云图，半圆管的布置方式与图5相对应。对于图7(b)和(e)，中间的半圆管正好位于相邻两挡板中间平面内，因此看上去比其他配置时“窄”了一块。为了便于说明，该处以标准配置为基准进行比较，对应截面内的流场情况见图3和图4。比较可知，半圆管的数量由6×4减为4×4后，对流场的影响可以忽略，说明原始配置时半圆管的数量过多；进一步减少半圆管的数量发现，虽然对主体区域内的流体没有明显影响，但搅拌槽内的低速区显著增加，说明4×4的数量具有明显的优势。此外，对比第一行和第二行子图还可以发现，在相同半圆管数量的前提下，当半圆管均匀布置时，能更有效地减少低速区。综合而言，以图5(d)所示的均匀布置的4×4的“波纹”内壁为最佳结构配置，此时每1/4搅拌槽内壁上所安装的相邻半圆管之间的夹角为18°。

图7 不同半圆管数量和安装位置时相邻两挡板中间平面内的速度云图

3.4 功率消耗

为了比较不同搅拌槽内壁结构形式时的功率，本文对功率准数Np进行了计算，方法与文献[18]一致，此处不再赘述。文献[24]指出，充分发展的湍流状态下标准挡板布置时Rushton桨搅拌槽的功率准数为4.8。然而需要说明的是，功率准数随桨叶厚度的增加而降低[25-26]，例如文献[21]没有考虑桨叶的厚度，给出的功率准数是5；文献[18]对一个几何相似的搅拌系统（但桨叶厚度不同，为t=0.03D，本文研究的搅拌系统中桨叶厚度为t=0.02D）进行实验测得的结果为4.81。

本文中，根据Fluent的模拟结果算得的光滑内壁搅拌槽的功率准数为5.63。对于该搅拌体系，Rutherford等[25]给出的实验测试结果为4.9，与该值相比，本文的模拟结果偏高约15%，这与事实相符。研究指出，标准-kε模型对功率准数的模拟结果偏高，例如Singh等[22]的模拟结果偏高约14%，Delafosse等[26]的模拟结果偏高约20%。对于图1所示的“波纹”内壁搅拌槽，采用相同方法算得的功率准数为5.72，约比光滑内壁搅拌槽的功率准数大2%；而对于均匀布置的4×4的最佳结构配置，其功率准数为5.68，与光滑内壁搅拌槽的功率准数非常接近，表明半圆管对搅拌功耗的影响可以忽略。

4 结 论

（1）“波纹”内壁结构不会改变搅拌槽内流体的流型，仍为典型的“双循环”流动结构。

（2）“波纹”内壁结构对流体的扰流作用能减小挡板后方的低速区域，增大搅拌槽顶部及壁面附近流体的速度，有助于提高流体混合均匀度。

（3）“波纹”内壁结构对湍动能的影响不明显，对搅拌功耗的影响也可以忽略。

（4）优化研究表明，半圆管半径越大，对流体的扰动越强，但对流体有效混合体积的削弱就越严重，以半圆管半径为挡板宽度的一半，即R=T/20为有效尺寸。

（5）当半圆管数量为4×4，且在搅拌槽内壁上均匀布置时，对流体的扰动程度最强，能有效地减少挡板后方及搅拌槽顶部区域内的流体低速区，为推荐最佳结构配置。

符 号 说 明

B——挡板宽度，m

C——桨叶离槽底高度，m

D——搅拌桨直径，m

H——液位高度，m

k——湍动能，m2/s2

l——桨叶长度，m

N——搅拌桨转速，r/s

Np——功率准数，量纲为1

Re——雷诺数，量纲为1

r——径向坐标，m

T——搅拌槽直径，m

t——厚度，m

ur——径向速度，m/s

utip——叶端速度，m/s

uz——轴向速度，m/s

uθ——切向速度，m/s

w——桨叶宽度，m

z——轴向坐标，m

ρ——液体密度，kg/m3

μ——动力黏度，Pa·s

θ——切向坐标，（°）

ε——湍动能耗散率，m2/s3

[1] Calabrese R V，Kresta S M，Liu M Y. Recognizing the 21 most influential contributions to mixing research[J/OL].Chemical Engineering Progress，[2014-01-31].http：//sip-trunking.tmcnet.com/ news/2014/01/31/7656910.htm.

[2] Aref H. Stirring by chaotic advection[J].J. Fluid Mech.，1984，143（1）：1-21.

[3] Ottino J M. The Kinematics of Mixing：Stretching，Chaos and Transport[M]. Cambridge，United Kingdom：Cambridge University Press，1989.

[4] Fountain G O，Khakhar D V，Ottino J M. Visualization of three-dimensional chaos[J].Science，1998，281：683-686.

[5] Alvarez M M，Shinbrot T，Zalc J，et al. Practical chaotic mixing[J].Chem. Eng. Sci.，2002，57（17）：3749-3753.

[6] Metcalfe G. Chaotic mixing - the first 25 years[C]//Proceedings of the International Symposium on Mixing in Industrial Processes ⅤⅢ （ISMIP8），Melbourne，Australia，15-17 September 2014.

[7] Smith J M. Reversible mixing impeller：US，5316443[P]. 1994-05-31.

[8] Bakker A，Ohio D. Impeller assembly with asymmetric concave blades：US，5791780[P]. 1998-08-11.

[9] 刘作华，郑雄攀，朱俊，等. 一种刚柔组合的搅拌桨：中国，201410017550.4[P]. 2014-04-16.

[10] Alvarez M M，Arratia P E，Muzzio F J. Laminar mixing in eccentric stirred tank systems[J].Can. J. Chem. Eng.，2002，80（4）：546-557.

[11] Wang S，Wu J，Ohmura N. Inclined-shaft agitation for improved viscous mixing[J].Ind. Eng. Chem. Res.，2013，52（33）：11741-11751.

[12] Komoda Y，Inoue Y，Hirata Y. Mixing performance by reciprocating disk in cylindrical vessel[J].J. Chem. Eng. Japan，2000，33（6）：879-885.

[13] 周慎杰，杨锋苓. 一类错位叶片式搅拌器：中国，201220750238.2[P]. 2013-06-19.

[14] Lamberto D J，Muzzio F J，Swanson P D，et al. Using time-dependent RPM to enhance mixing in stirred vessels[J].Chem. Eng. Sci.，1996，51（5）：733-741.

[15] Kadic E，Heindel T J. An Introduction to Bioreactor Hydrodynamics and Gas-Liquid Mass Transfer[M]. Hoboken，New Jersey：John Wiley & Sons，Inc.，2014.

[16] Streak F，Karcz J. Experimental studies of power consumption for agitated vessels equipped with non-standard baffles and high-speed agitator[J].Chem. Eng. Process.，1993，32（6）：349-357.

[17] 戴干策，陈剑佩，张家庭，等. 具有槽缝挡板的搅拌反应器：中国，02265664.2[P]. 2002-07-22.

[18] 杨锋苓，周慎杰，王贵超，等. 非标准挡板搅拌槽内湍流流场的数值模拟[J]. 高校化学工程学报，2012，26（6）：952-958.

[19] 王星星，刘志炎，龙伟民，等. 椭圆底封头十字形挡板搅拌釜内流畅研究[J]. 机械工程学报，2014，50（6）：156-164.

[20] Alvarez M M，Zalc J M，Shinbrot T，et al. Mechanisms of mixing and creation of structure in laminar stirred tanks[J].AIChE J.，2002，48（10）：2135-2148.

[21] Wu H，Patterson G K. Laser-Doppler measurements of turbulent-flow parameters in a stirred mixer[J].Chem. Eng. Sci.，1989，44（10）：2207-2221.

[22] Singh H，Fletcher D F，Nijdam J J. An assessment of different turbulence models for predicting flow in a baffled tank stirred with a Rushton turbine[J].Chem. Eng. Sci.，2011，66（23）：5976-5988.

[23] Murthy B N，Joshi J B. Assessment of standardk-ε，RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs[J].Chem. Eng. Sci.，2008，63（22）：5468-5495.

[24] Couper J R，Penney W R，Fair J R，et al. Chemical Process Equipment：Selection and Design[M]. 3rd ed. Waltham，USA：Butterworth-Heinemann Co.，2012.

[25] Rutherford K，Mahmoudi S M S，Lee K C，et al. The influence of Rusthon impeller blade and disk thickness on the mixing characteristics of stirred vessels[J].Chem. Eng. Res. Des.，1996，74（3）：369-378.

[26] Delafosse A，Lin A，Morchain J，et al. LES and URANS simulations of hydrodynamics in mixing tank：Comparison to PIV experiments[J].Chem. Eng. Res. Des.，2008，86（12），1322-1330.