统一强度安全系数法在隧洞围岩稳定评价中的应用

□王冬林 □张子建 □李虎星

（河南省水利科学研究院河南省水利工程安全技术重点实验室）

0 引言

在岩石力学以及工程结构的有限元弹塑性分析中，与Mohr-Coulomb、Drucker-Prager强度理论相比，统一强度理论具有统一的模型，统一的数学表达式，易于在弹塑性有限元程序中实施[1]。现有商业有限元软件中的岩土材料本构模型，尚未包括统一强度理论的弹塑性本构模型，ADINA软件业也不例外。尝试编写Fortran程序对材料的本构进行二次开发，因不能与ADINA接口程序和输出程序建立良好衔接而未能实现。为了能够借助统一强度理论这一重要的本构关系，建立适用于各种岩土材料的统一强度准则安全系数法，并能实现有限元数值分析计算，故开展以下研究工作。

根据统一强度理论推导弹塑性本构矩阵，结合统一强度安全系数的定义，编写相应的Fortran计算程序，并验证该程序的可靠性。利用自编程序对隧洞算例进行有限元数值分析和点计算安全系数计算，并结合Surfer软件处理数据结果。与ADINA有限元软件的分析结果进行比较，比较不同屈服条件下安全系数的计算结果，分析安全系数法的优点，以及统一强度理论的优缺点。

1 统一强度理论条件下的安全系数定义

统一强度理论考虑了所有应力分量以及它们对材料屈服、破坏的不同影响，当α 和β 取值不同时，统一强度理论可以简化为不同屈服准则的强度理论。统一强度点安全系数计算结果如下

2 统一强度理论的弹塑性本构模型及程序设计

2.1 增量理论

任一点的应变增量由弹性应变增量和塑性应变增量两部分构成[3]，应力增量与应变增量的关系式表示为

κ 值与塑性应变有关，满足加载条件

对于理想的塑性体，A=0，由塑性力学可知，在相关联的流动法则下的塑性本构关系成立时，Q=F。一般情况下，Q≠F，塑性势函数通常也表示为Q（I1，J2，J3），它的计算与相同，只需要把F换成Q。因此下面主要介绍｝的计算。

统一强度理论的应力不变量表达式为

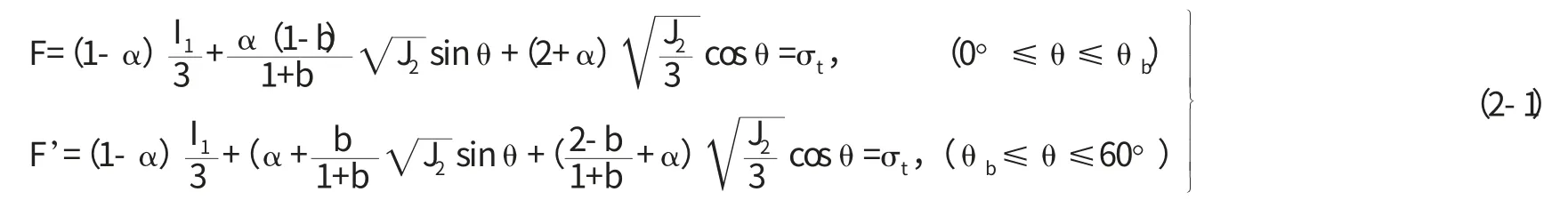
对于三维问题,通常，用I1、J2、J3等表示加载函数为，因此

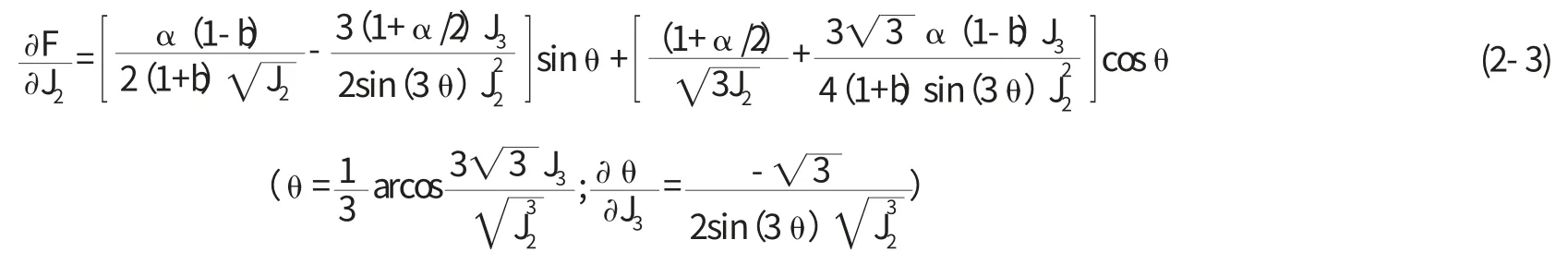
同理

1.人生三截草，不知哪截好。（人有旦夕祸福，人生也难以预测，将人生几个阶段比喻成三截草，不知道哪个阶段生活会怎么样。）

2.3 有限元程序设计与应用

根据统一强度理论弹塑性本构矩阵以及统一强度安全系数的定义，编写设计了可以应用于各种屈服准则包括统一强度理论的Fortran程序。从程序的设计流程、相关代码，可知该程序从输入数据的格式、功能等方面进行了改进，增加了统一强度准则。提供了多个屈服准则的选择，不同材料可采用不同屈服准则，而且对于不同模型表达式，也便于修改，并且将线性计算和非线性计算的收敛判据扩展为4种。主要子程序流程有：

子程序INPUT是读入输出程序计算中的结构控制参数、单元相关信息、结点坐标系、结点约束信息和材料的性能参数，并能计算结构的约束自由度数及总自由度数，并能调用GAUSSSQ程序计算高斯积分点的位置。

子程序INVAR是计算等效应力或应力偏量及其相应函数值。运行中根据变量MNCRIT的不同选用不同的屈服准则，1——Tresca准则；2——VonMises准则；3——Mohr-Coulomb准则；4——Drucker-Prager准则；5——UnifiedStrengthTheory准则。

子程序YIELDF的作用是分别计算流动矢量VECA1、VECA2、VECA3和AVECT。

子程序FLOWPL的作用主要是根据不同分析类型计算塑性应变率。

子程序STIFVP的作用是依次计算每个单元的刚度矩阵。

子程序FRONT的作用是用波前法求解方程组。

3 算例分析

表1 模型物理力学参数表

图1 网格划分后的几何模型图

结合Surfer图形软件处理数据结果，绘制安全系数等值线图，使得计算结果能以图像的形式直观呈现，计算结果见图1。与ADINA有限元分析软件计算的Mohr-Coulomb安全系数结果进行比较分析，分析统一强度安全系数法的优缺点。

图2 统一强度安全系数分布图

图3 Mohr-Coulomb安全系数分布图

从图2和图3可以看出，统一强度理论和Mohr-Coulomb强度准则的计算结果相近，其安全系数分布规律一致，最小安全系数出现在洞顶位置，分别为0.15和0.17；距洞顶约2倍高度处等值线高度密集，且安全系数均在1.00左右，红色区域安全系数最大，最大值分别为1.48和2.25；洞室左右肩线上计算的安全系数等值线由密到疏，数值由小变大。对最可能发生破坏的洞顶中心上的安全系数进一步观察分析，发现在洞顶附近约1倍洞高范围内，统一强度理论计算的点安全系数比相同位置处Mohr-Coulomb强度理论计算的安全系数小，而在此范围之外一直到红色密集区域，统一强度理论计算的点安全系数比相同位置处Mohr-Coulomb强度理论计算的安全系数。偏小为了进一步研究产生该现象的原因，选取洞室右肩线上的O-O截面，对比分析不同强度理论该截面上安全系数大小和发展规律，见图4。

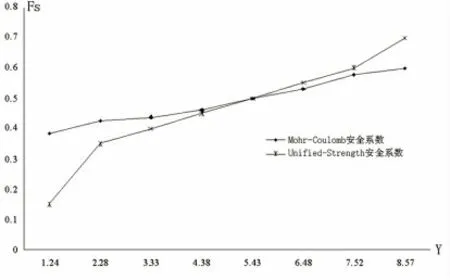
图4 不同屈服准则O-O截面安全系数图

在图4中，水平坐标取5.43m时，两者的安全系数一样大；Y<5.43m时，统一强度安全系数小于Mohr-Coulomb安全系数，Y>5.43m时，统一强度安全系数反而大于Mohr-Coulomb安全系数。说明该现象不只在对洞顶中心线上的安全系数的分析时发生，有一定的必然性。由此可见，统一强度安全系数确定的不稳定范围小于Mohr-Coulomb安全系数给出的不稳定范围。俞茂宏（2005）曾指出统一强度理论计算得到的塑性区范围比Mohr-Coulomb强度理论小，也就是说发生破坏的范围较小，这与分析结果一致。但是，分析还表明，不能简单的认为塑性区破坏范围小得到的安全系数就大。与Mohr-Coulomb强度理论计算安全系数比较，统一强度安全系数法确定的隧洞围岩失稳破坏范围更加合理[5]。在工程结构的强度研究中，统一强度理论计算结果可以节省工程预算和投资。

4 结语

（1）理论分析表明统一强度理论是包含了一系列连续变化的屈服准则系统，根据弹塑性增量理论建立统一强度理论弹塑性本构模型，在此基础上结合统一强度安全系数的定义编写了适用于不同屈服准则的有限元程序。

（2）提出以统一强度安全系数对隧洞围岩稳定作出评价的方法。利用自编程序分析计算了隧洞的围岩稳定安全系数，通过SURFER软件对输出结果整理绘制安全系数等值线图。采用统一强度理论的结果与Mohr-Coulomb强度理论的结果相近，最小安全系数和最大安全系数出现位置相同，两者安全系数分布规律基本一致，表明该程序具有一定的通用性。

（3）研究表明，统一强度安全系数确定的破坏范围，与Mohr-Coulomb安全系数计算的不稳定范围相比偏小。统一强度安全系数法应用于工程结构的强度研究中，可以节省工程预算和投资。

[1]潘晓明，孔娟，杨钊.[J].岩土力学，2010，31（4）：1092-1098.

[2]俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报，1994,16（2）：1-10.

[3]张学言，闫澍旺.岩土塑性力学基础，第2版[M].天津：天津大学出版社，2004（9）.

[4]俞茂宏，OdaY，盛谦，等.统一强度理论的发展及其在土木水利等工程中的应用和经济意义[J].建筑科学与工程学报，2005,22（1）：24-38.

[5]王冬林.基于安全系数法的地下洞室围岩稳定评价方法研究[D].西北农林科技大学水利与建筑工程学院，2012.