我国不同时期证券收益率波动特征研究

唐欢

摘要：经济全球化的发展促进了世界资源配置的优化并提高了金融业的运行效率，但同时也降低了金融体系的稳定性、加劇了金融市场的波动性和市场风险。我国的证券市场充满着不确定性，市场形势处于不断变化的状态。借鉴国内外的研究成果，通过GARCH族模型进行实证分析，从描述统计和经济计量角度刻画证券上证综合指数收益率波动的特征，进而总结出我国证券市场中收益波动的统计特征。为了提高模型和研究结果的可靠性和精度，将我国1996年股市改革以及2008年金融危机作为分界点，对自我国股票市场建立（1990年12月19日）至今（截止至2015年3月2日）一共5880个数据进行分段分析，总结得出各不同阶段我国证券市场波动的特点。

关键词：GARCH族模型；证券收益率；中国证券市场

中图分类号：F2文献标识码：A文章编号：16723198（2015）17001604

1引言

金融市场充满着不确定性，市场形势处于不断变化的状态。随着社会的飞速发展，信息的传播以及资本流动的频繁使得证券价格不断变化。同样的，不断变化的证券价格反作用于市场，二者相互影响相互传导。与国外发达国家的证券市场相比，我国证券市场起步较晚，处于尚未成熟的发展阶段，我国的证券市场中个人投资者占据主要地位，而投资机构的力量相对薄弱。个人投资者在专业知识、信息获取等方面的限制，因此在个人投资者为主导的环境下，我国的证券市场带着明显的投机色彩。加之个人投资者非理性的跟风，我国的证券市场常常处于无序并且波动剧烈，常伴随股票价格大起大落的现象，高风险特征明显。

证券市场的波动通常具有异方差性。波动的方差代表市场的风险，因此异方差建模对风险分析和资本定价具有重要的意义。证券价格的时间序列数据方差随着时间的变化而变化，表现在波动集群，持久记忆和尖峰厚尾现象。传统的时间序列模型（ARMA）模型是基于方差不变的假设，难以刻画证券价格的变化。Engle（1982）提出自回归条件异方差ARCH模型，把方差和条件方差区分开，使条件方差作为误差的函数，成功地刻画条件异方差的情况。Bollerslev（1986）在ARCH模型的基础上提出GARCH（广义自回归条件异方差）模型，让条件方差作为过去误差和滞后条件方差的函数而变化，更好地体现出波动聚集效应。由于证券价格波动对市场下跌的反应常表现为比对市场上升的反应剧烈，这种反映的非对称性反应成为“杠杆效应”，Nelson（1991）提出的ENGARCH模型和TGARCH模型，通过引入虚拟变量区分市场下跌和上升两种情形，得到具有杠杆效应的波动率。由于金融资产的收益性常常与其风险成正比，于是Engle、Lilien、Robins（1987）提出GARCH-M模型，将条件异方差引入收益的估计模型。GARCH族模型可以对证券市场波动进行准确地解释。

上海证券市场开市早，市值高，稳定性较强，因此在探究我国证券市场的过程中具有代表性。本文则是通过引入最新的数据（1990—2015年上证综合指数日数据），以1996年股票市场改革以及2008年金融危机为分界点以上证综合指数为代表，运用GARCH族模型对我国证券市场收益率波动进行实证分析。本文通过研究我国上证综合指数收益率波动的统计特征，建立描述波动率变化的模型，通过了解证券价格波动的规律，探究价格波动的不对称性，掌握我国市场存在杠杆效应，以及风险对收益率的影响，对我国证券市场的的监管部门以及广大的投资者都具有很大的意义。

2实证分析

2.1数据说明

本文选取了从上海证券交易所开市（1990年12月19日）至今（截止至2015年3月2日）一共有5880个上证综合指数日数据。

1996年12月16日起，我国股市进行重大改革，开始实行T+1交易制度，以及实施涨跌停板限制。2008年，世界性金融危机袭来，中国证券市场受到重大冲击。因此，本文以1996年12月16日和2008年12月31日为分界点，通过多时间段对比，分析出我国不同阶段证券市场收益率波动的情况。

上证综合指数日数据均来自WIND数据库。数据处理与分析采用软件为Eviews6.0与SPSS17。

在本文的分析研究中，假设sht为t期上证综合收盘指数，在探讨金融资产价格变化的时候，通常采用对数收益率进行描述：

dlnsht=lnsht-lnsht-1

其中sht-1为上一期的上证综合指数，从而算出不同时期段上证综合指数的对数收益率。

2.2描述性统计分析

1990年12月19日到1996年12月14日的对数收益率统计分布如图1所示。该阶段上证综合指数对数收益率峰度93.10，远远偏离正态分布。另外，收益图呈现显著右偏趋势，偏度达到5.34，可知在我国股市建立初期市场活跃，表现出明显的正收益。根据统计图可得知在未实行涨停制度以及T+1制度之前，整个股票市场不成熟，不稳定，异常波动可能性大，因此在下文模型建立中将排除这一阶段数据。

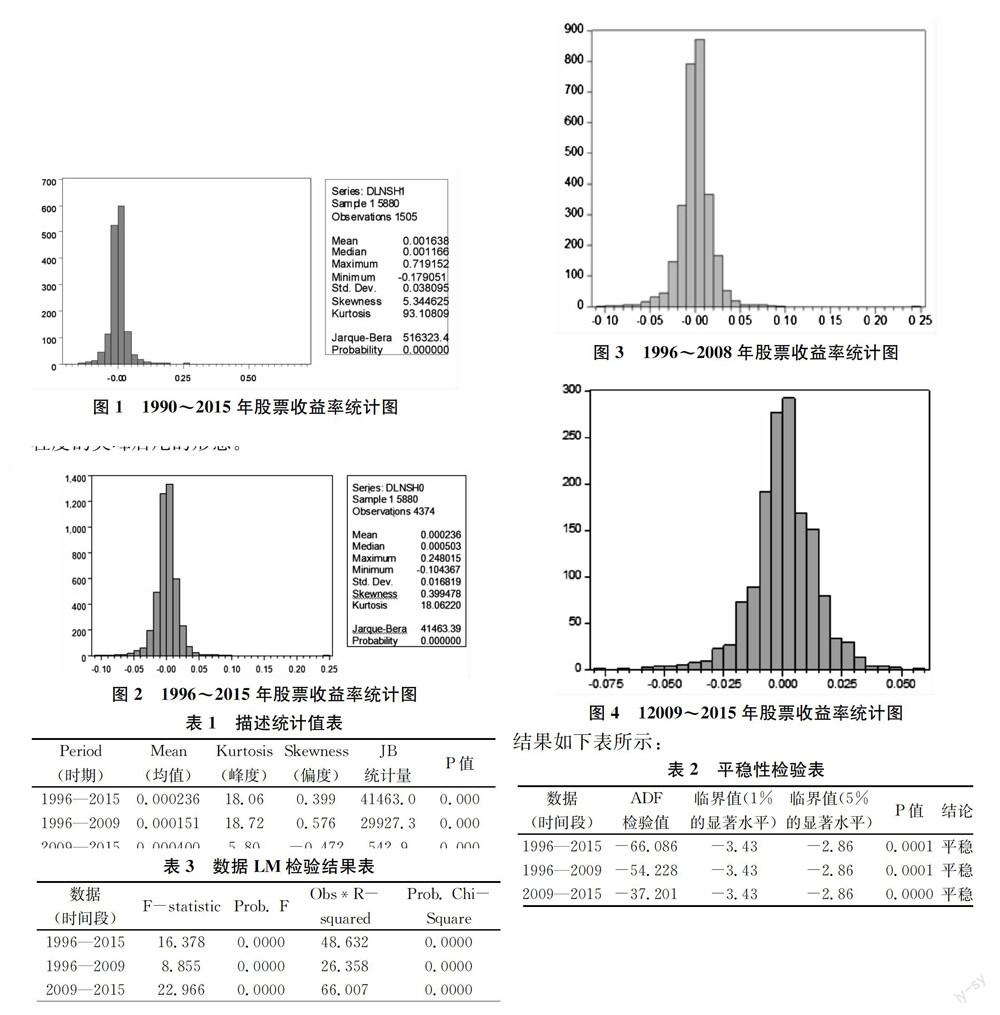
图11990～2015年股票收益率统计图自1996年12月16日股票市场改制到最近2015年3月2日共4374个上证综合指数收盘日数据对数收益率描述统计分析如图2所示，该时间段上证综合指数对数收益率峰度18.06，偏度为0.399，呈现正偏态。

根据2008年世界金融危机爆发对我国证券市场产生巨大的冲击，因此以2008年金融危机为分界点对我国证券收益率进行分析描述统计分析如图3和图4所示。1996年到2009年（金融危机爆发及之前），我国证券对数收益率均值为0.000151，峰度为18.72，偏度为0.576，呈现正偏态。2009年到2015年（金融危机爆发之后至今），我国证券对数收益率均值为0000400，较之于金融危机前期有所上升；峰度为560，高峰集群分布效应有所缓解；偏度为-0.472，呈现负状态。

由JB统计量得知，各个不同时间段的上证综合指数对数收益率均不服从正态分布的假设，均呈现一定程度的尖峰后尾的形态。

图21996～2015年股票收益率统计图图31996～2008年股票收益率统计图图412009～2015年股票收益率统计图表1描述统计值表

2.4ARCH效应的检验

对1996—2015年上证综合对数收益率，分阶段1996—2009，2009—2015年上证综合对数收益率利用ARMA（1，1）模型dlnsht=φdlnsht-1+ut+θut-1进行拟合，对其残差平方进行ARCH效应LM检验。

根据条件异方差ARCH LM检验可得当滞后阶数为3时三个时间段的数据均存在条件异方差，因此需要运用条件异方差模型分别对其进行拟合，结果如表3所示：

表3数据LM检验结果表

数据

（时间段）F-statisticProb. FObs*R-

squaredProb. Chi-

Square1996—201516.3780.000048.6320.00001996—20098.8550.000026.3580.00002009—201522.9660.000066.0070.00002.5GARCH族模型

2.5.1GARCH（1，1）模型拟合结果

根据残差平方的自相关和偏自相关图的分布情况，决定用GARCH（1，1）对三个时间段数据进行条件异方差进行拟合。

（1）从总体上分析看，1996—2015年上证综合指数对数GARCH（1，1）收益率方差方程：

2t=-4.45×10-5+0.1328u2t-1+0.85932t-1（9）

t= 36.17270.92

（p=0.000）（p=0.000）

AIC=—5.57SC=—5.56

（2）分时段来看，1996—2009年，2009—2015年上证综合指数对数收益率GARCH（1，1）方差方程为：

1996—2009年：

2t=1.48×10-6+0.2602u2t-1+0.73882t-1（10）

t=30.1876.50

（p=0.000）（p=0.000）

AIC=—5.42SC=—5.42

2009—2015年：

2t=2.21×10-6+0.0512u2t-1+0.93672t-1（11）

t=7.31095.427

（p=0.000）（p=0.000）

AIC=-5.89SC= -5.87

表4GARCH（1，1）模型拟合后LM检验结果

时期F-

statisticProb.FObs*R-

squaredProb.F1996-2015年0.31700.8131（不显著）0.95170.8129（不显著）1996-2009年0.32770.8053（不显著）0.98410.8051（不显著）2009-2015年0.80720.4899（不显著）2.42410.4289（不显著）根据上表可知，LM检验统计量均不显著，说明各时期的拟合模型残差序列不存在ARCH效应。

根据模型结果，我们可以得到：

（1）从总体上看，1996-2015年拟合模型中，ARCH项和GARCH项的系数之和+=0.1328+08591=0.9921<1，满足参数约束条件。又由于系数非常接近于1，表明条件方差所受的冲击具有持久性，及冲击对未来所有预测都具有重要的作用。

（2）分时期分析，在金融危机之前，1996-2009年数据的模型中，ARCH项和GARCH项的系数之和+=0.2610+0.7388=0.9998<1.000。非常接近于1，表明條件方差所受的冲击具有持久性。

（3）分时期分析，在金融危机之后，2009-2015年数据的模型中，ARCH项和GARCH项的系数之和+=0.0512+0.9367=0.9879<1，满足参数约束条件。又由于相对于总体数据（1996—2015年）来说，系数之和0.9879<0.9998，说明在金融危机之后，我国证券市场处于恢复状态，活跃性降低，因此波动率的冲击的持续性有所降低。

2.5.2EGARCH模型拟合结果

基于股市“杠杆效应”的假设，在此建立非对称EGARCH模型对三个时期的数据进行拟合比较，如下所示：

（1）从总体上分析看，1996—2015年上证综合指数对数EGARCH收益率方差方程：

ln（2t）=-0.4215+0.2476|t-1/t-1|-0.0086（t-1/t-1）+0.9712ln（2t-1）（12）

（2）分时段来看，1996—2009年，2009—2015年上证综合指数对数收益率EGARCH方差方程为：

1996—2009年：

ln（2t）=-0.6402+0.3452|t-1/t-1|-0.0074（t-1/t-1）+0.9526ln（σ2t-1）（13）

2009—2015年：

ln（2t）=-0.2272+0.1296|t-1/t-1|-0.0092（t-1/t-1）+0.9851ln（σ2t-1）（14）

根据模型结果，我们可以得到：

（1）从总体上看，1996-2015年的拟合的EGARCH模型中，α的估计值为0.2476，非对称项γ的估计值为-0.0086。当μt-1>0时，该信息冲击对条件方差的对数有一个0.2476-0.0086=0.239倍的冲击；当ut-1<0时，它给条件方差的对数带来的冲击大小为0.2476+0.0086=0.2562倍。

（2）分时期分析，在金融危机之前，1996-2009年数据的EGARCH模型中，α的估计值为0.3452，非对称项γ的估计值为-0.0074。当ut-1>0时，该信息冲击对条件方差的对数有一个0.3452-0.0074=0.3378倍的冲击；当ut-1<0时，它给条件方差的对数带来的冲击大小为0.3452+0.0074=0.3526倍。

（3）分时期分析，在金融危机之后，2009-2015年数据的EGARCH模型中，α的估计值为0.1296，非对称项γ的估计值为-0.0092。当ut-1>0时，该信息冲击对条件方差的对数有一个0.1296-0.0092=0.1204倍的冲击；当ut-1<0时，它给条件方差的对数带来的冲击大小为0.1296+0.0092=0.1388倍。对比分析可知，在金融危机之后，上证综合指数对数收益率的波动减小，但是值得注意的是其“杠杆效应”确实增大的，0.0092>0.0074。表明人们在金融危机之后对“利坏消息”的反映变得更加敏感。

2.5.3GARCH-M模型的拟合结果

根据金融理论中收益与风险应当成正比的理论，风险越大，预期收益越高。利用GARCH-M模以条件方差表示预期风险，对三个时期的数据进行拟合，拟合结果（采用条件标准差模型拟合）如下所示：

（1）从总体上分析看，1996—2015年上证综合指数对数收益率GARCH-M方程：

d ln sht=-0.00035-0.7564d ln sht-1+01110t+t+0.7888t-1（15）

2t=6.39×10-6+0.1364u2t-1+0.85472t-1（16）

（2）分时段来看，1996—2009年，2009—2015年上证综合指数对数收益率GARCH-M方程为：

1996—2009年：

d ln sht=-0.000468-0.7806d ln sht-1+01475t+t+0.8149t-1（17）

2t=1.59×10-5+0.2745u2t-1+0.72612t-1（18）

2009—2015年：

d ln sht=-0.000987+0.1303d ln sht-1+00943t+t-0.0887t-1（19）

2t=2.28×10-6+0.05278u2t-1+0.93492t-1（20）

从GARCH-M模型可以看出，在三个阶段数据建立的方程中ρ分别为0.1110，0.1475，0.0934，均为正数表明指数的对数收益率与预期风险即波动率成正相关。

（1）从总体上看，1996-2015的拟合的GARCH-M模型中，ρ=0.1110，表明在这期间预期风险每增加一个单位，收益率也相应增加0.111个百分点。

（2）分时期分析，在金融危机之后，2009-2015年数据的GARCH-M模型中，ρ=0.1475，表明在金融危机前，股市的预期风险每增加一个单位，收益率也相应增加0.1475个百分点。

（3）分时期分析，在金融危机之后，2009-2015年数据的GARCH-M模型中，ρ=0.0934。相较于金融危机之前，股市的收益率对预期风险的反映程度减小，预期风险每增加一个单位，收益率相应增加0.0934个百分点。

3研究结论

第一，我国证券收益率序列的方差随时间变化，并且有时变化很剧烈，存在显著异方差现象。根据统计分析，从1990年我国初步建立证券市场到1996年我国未实行为恢复涨停制度之前，其统计分布的峰度远远偏离正态分布，峰度达到93.10，偏度达到5.34，呈现显著正偏态，表明我国证券市场在成立处理发展迅速，收益高，异常波动影响严重，因此投机性大。我国证券市场我国自1996年股市改革至今，上證综合指数对数收益率分布的峰度达到18.06，具有尖峰厚尾的性质，呈现轻微正偏态。相对于证券市场建立初期，这一阶段证券价格波动趋于缓和，反映我国证券市场正处于稳健发展的状态。

第二，证券收益率具有冲击持续性。从GARCH（1，1）模型得知，各模型系数之和十分接近于1，表明信息在股市中衰减得很慢，前期信息对后期的影响作用是长久的。从总体上看，1996年到2015年GARCH（1，1）系数之和为0.9921，这表明我国股市条件方差所受的冲击具有持久性，冲击衰减速度非常慢，对未来所有预测都具有重要的作用。在金融危机之前，GARCH（1，1）模型系数之和为0.9998，大于1996-2015年总体水平，然而金融危机之后，GARCH（1，1）的系数之和为0.9879，小于1996-2015年总体水平。这表明，纵然信息在股市中衰减速度很慢具有很大的持续性，但是自金融危机之后，我国证券市场的收益率对信息冲击的敏感性有所降低。

第三，证券收益率具有杠杆效应。信息对股票市场波动的非对称性影响称为杠杆效应。EGARCH模型都反映了市场对信息的非对称性的反映。根据不同时间段的数据拟合模型中非对称项的系数为均显著，这表明我国证券市场中存在显著的杠杆效应。值得注意的是，在金融危机前后，EGARCH模型中的非对称想系数明显的差异。这表明在金融危机后，市场对于利坏消息反映更为剧烈，投资者相对于危机爆发之前显得更为小心谨慎。

第四，金融资产的收益率与风险程度呈现正相关。从GARCH-M模型可以发现利用条件标准差对收益率进行预测效果显著。因此GARCH-M模型充分揭示了我国金融市场中收益率和风险程度的密切关系。比较金融危机前后，我国证券市场收益率对于预期风险的反映，我们可以发现，在金融危机之后当预期风险增大是收益率增长程度减小。这反映了在金融危机之后整个证券市场投机性降低，投资者的投资的风险偏好程度减小，整个证券市场的投资行为趋于理性。

參考文献

[1]高铁梅.计量经济分析方法与建模：Eviews应用及实例（第2版）[M].北京：清华大学出版社，2009.

[2]王燕.应用时间序列分析（第二版）[M].北京：中国人民大学出版社，2009.

[3]陶佶.沪深300股指期货：理论和实务[M].北京：中国发展出版社，2008：81218.

[4]刘鸿儒.股指期货热点问答[M].北京：中国金融出版社，2009：5170.

[5]肖辉，刘文财.股票指数现货市场与期货市场关系研究[M].北京：中国金融出版社，2006：247263.

[6]彭红枫，叶永刚.基于修正的ECMGARCH模型的动态最优套期保值比率估计及比较研究[J].中国管理科学，2007，（05）：2935.

[7]刘国旗.非线性GARCH模型在中国股市波动预测中的应用研究[J].统计研究，2000，（01）：4952.

[8]江孝感，万蔚.马尔科夫状态转换GARCH模型的波动持续性研究——对估计方法的探讨[J].数理统计与管理，2009，（04）：637645.

[9]Fair，R1C1，Shiller.R1J1，1the information content of exante forecasts Review of Economics and Statistics[J].1989：3253311.

[10]Franses， P1H1.Time Series Models for Business and Economic Forecasting[J].1998.

[11]Li，W.K.，Ling S.，Michael，M..Recent Theoretical Results for Time Series Models with GARCH Errors[J].Journal of Economic Survey，2002，16（3）：245269.

[12]Engle R F.. Autoregressive Conditional Heteroskedasticity with Estimates of the VARiance of United Kingdom Inflation[J].Econometrica，1982，50（7）：203224.

[13]Nelson， Daniel B，Conditional Heterosdasticity in Asset Returns： A New Approach[J].Econometrica，1991， 59：347370.

[14]Enlge Robert， David M. Lillien and Russell P. Robins. Estimating Time Varying Risk Premia in the Term Structure： The ARCH-M Model[J].Econometrica，1987，55：391406.