L波段雷达电离层高速运动目标ISAR成像补偿方法

黄小红文贡坚

（国防科技大学自动目标识别重点实验室 长沙 410073）

L波段雷达电离层高速运动目标ISAR成像补偿方法

黄小红*文贡坚

（国防科技大学自动目标识别重点实验室 长沙 410073）

目标高速运动和电离层效应都会对低频段宽带线性调频雷达信号的相位产生调制现象，进而降低逆合成孔径雷达（ISAR）成像分辨率。为得到清晰的目标 ISAR图像，需有效消除这两者对目标回波的影响。该文首先建立电离层高速运动目标回波的信号模型，再根据目标回波为高阶多项式相位信号的特点，提出基于离散多项式变换的高阶相位估计算法，利用高阶相位估计值进行回波信号相位调制分量补偿，实现ISAR成像的自聚焦。仿真实验表明，该算法可以准确估计回波信号高阶相位参数，提高ISAR成像质量。

逆合成孔径雷达；电离层；多项式相位信号；运动补偿

1 引言

对目标进行逆合成孔径雷达（ISAR）成像，是空间目标识别的重要途径之一。逆合成孔径雷达成像运动补偿算法已有许多研究成果［1-6］，可以实现3维运动目标和机动目标成像。L波段是空间目标成像探测雷达常用的波段之一，利用地基L波段雷达对高速运动目标进行ISAR成像时需解决的两个关键问题：一是目标高速运动对回波相位调制效应的校正，二是电离层效应的校正。

空间目标成像雷达通常采用具有大时宽-带宽积的线性调频（LFM）雷达信号，研究表明［7］，当目标运动速度较高时，往往会产生脉内走动现象，表现形式为目标回波相位调制效应。文献［8］针对X波段雷达提出了先估计目标运动速度在进行相位补偿的校正方法，文献［9］提出了基于立方相位函数参数估计的空间目标运动补偿方法。

此外，低轨空间目标都处于电离层（约60～2000 km）之中，雷达发射信号和目标反射的雷达信号在大气中传播穿过电离层时，雷达信号与电离层中带电粒子相互作用，导致电磁波的延时、色散、衰减以及折射等，这些会导致目标ISAR成像分辨率和图像质量下降。研究表明［10，11］，当成像雷达系统的工作频段较高时，可以忽略电离层对成像系统的影响，当雷达工作于L波段、P波段甚至更低频段时，需考虑电离层对成像系统的影响。随着雷达成像技术的发展和用户对成像质量不断提升的要求，电离层对宽度雷达系统的影响研究也不断升温。从电波传输路径的角度来看，电离层对星载SAR和地基ISAR的影响是等同的。在星载雷达方面，针对电离层校正问题，文献［12］讨论了天基SAR 测量中的Faraday旋转效应及其补偿技术，提出利用裂谱处理和GPS测得的全球电离层积分电子总量（TEC）分布图进行距离和方位压缩中的相位修正。文献［13］提出了采用HF-SAR 对电离层分层成像的研究方法。文献［14］采用PGA方法对OTHR 雷达的电离层相位污染进行校正。文献［15］研究了利用星载L波段全极化SAR数据法拉第旋转效应测量电离层的方法。

在地基雷达方面，文献［13］和文献［10］分别研究了电离层对VHF 波段和L波段的地基雷达对空间目标ISAR 成像时的电离层影响。文献［10］给出了基于双频测量的地基L波段ISAR电离层效应校正方法，文献［16］针对P波段雷达提出了一种利用多个频点回波信号相位反演电离层TEC 的测量方法。

从已发表的文献来看，目标高速运动效应和电离层效应的校正已有许多研究成果，但这些方法都将这两种现象孤立看待，而且只针对其中一个问题进行了研究。事实上，这两种现象对电离层高速运动目标宽带1维距离像的影响是同时存在的，因此进行高分辨ISAR成像时需同时考虑这两方面的影响。

本文以L波段宽带线性调频雷达信号为例，研究目标高速运动和电离层对宽带雷达信号的影响，建立了电离层高速运动空间目标回波信号模型，根据模型特点提出了基于离散多项式相位变换（DPT）的电离层高速运动目标高阶相位估计算法，实现了目标自聚焦成像，该方法不需估计目标运动速度和电离层电子密度和电子总量。最后给出了数值仿真结果，验证了算法的有效性。

2 电离层高速运动目标回波模型

当雷达发射信号为宽带线性调频信号时，为了降低数据采样率，常采用去斜率的方式进行处理，即用发射信号或重新产生的 LFM 本振信号与目标回波混频。

雷达发射的脉宽为T，带宽为B的线性调频信号为

其中，fc为雷达发射信号载频，r （·）为发射信号的矩形包络，调频斜率为 K = B/T，发射信号经目标的各强散射点反射后，雷达接收到的回波信号为

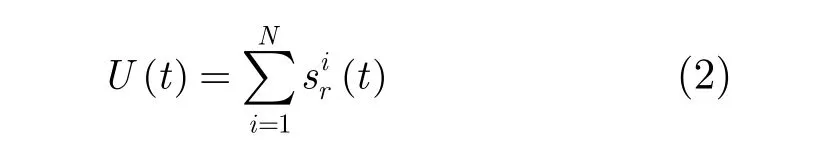
N为刚性目标包含的强散射点个数。为了描述方便，先考虑一个强散射点的情况。根据文献［7］和文献［10］研究结果，雷达发射信号经该强散射点反射后，回波信号为

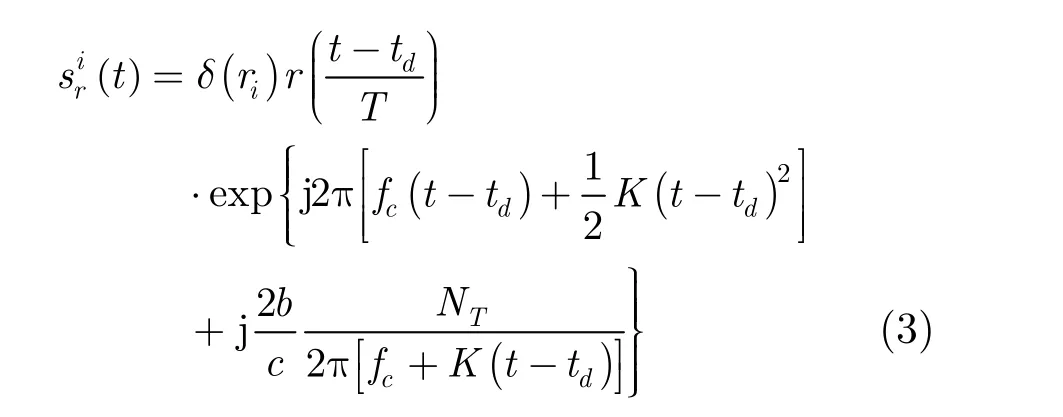
其中，td为目标回波延时， NT积分电子含量，b= e2/2 ε0m = 1.591 × 103m3/s2，为一个常数，这里e是电子电量， ε0是自由空间介电常数，m是电子质量。将式（3）中相位第3项利用泰勒公式展开得到

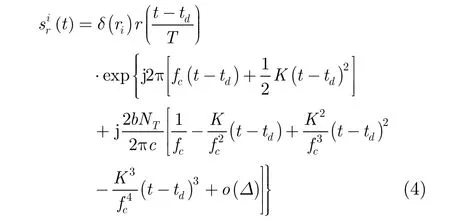
设去斜率处理时参考信号为

其中， t0为参考信号延时，回波信号与参考信号共轭相乘得

假设目标径向速度为V，加速度为a，代入式（6）得：

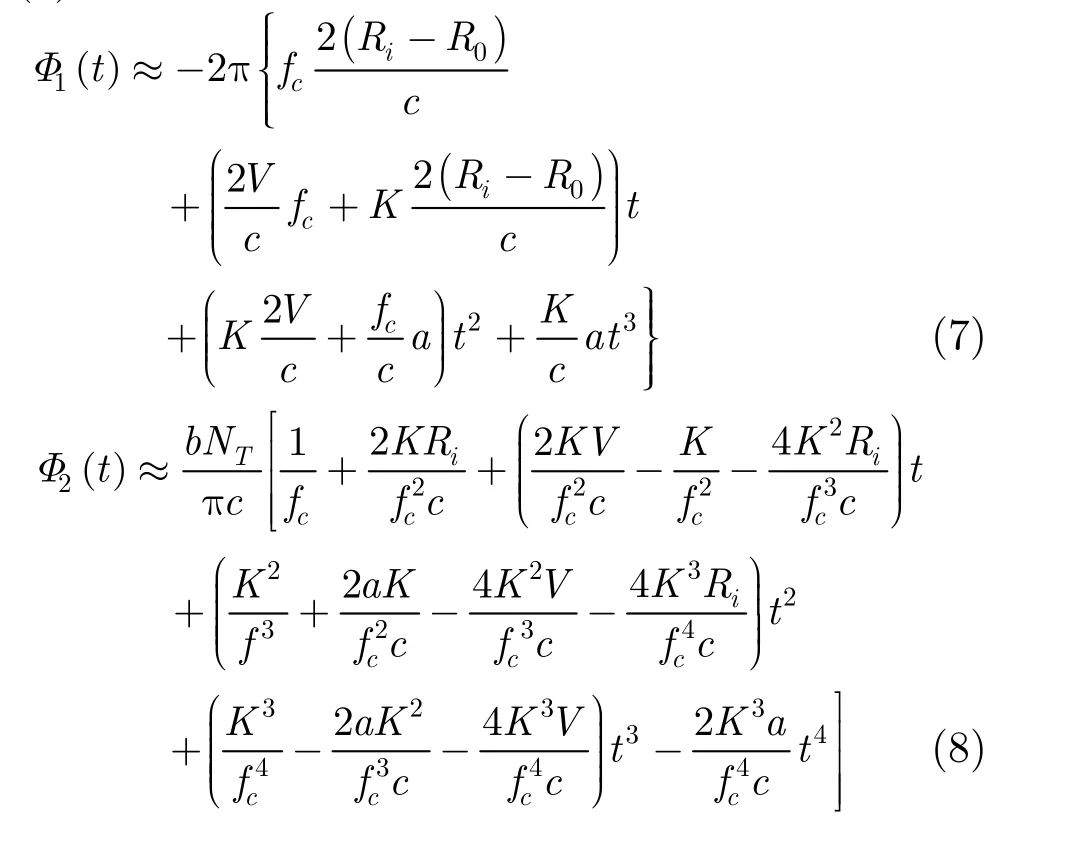
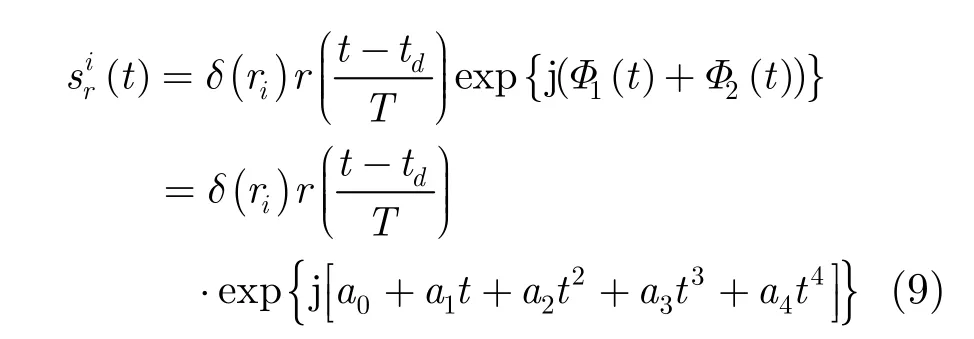
其中

包含N个强散射点的第m次目标回波信号为

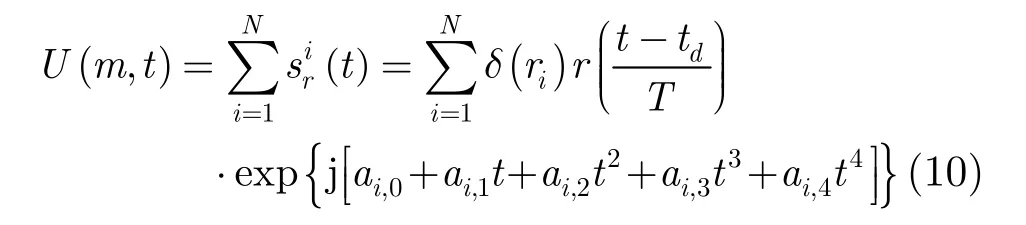
3 基于DPT的高阶相位补偿方法

由式（10）可知，由于电离层和高速运动的影响使得目标回波信号相位出现高次项，高次项将导致目标1维距离像产生畸变，为此需进行高次相位补偿，实现目标距离像的校正。对这种多分量多项式相位信号的参数估计，文献［17］和文献［18］分别给出了基于多项式变换和模糊函数的多项式信号参数估计方法，它们对信号噪声比较敏感，而且计算复杂。

从式（10）可以看出，高阶相位系数与雷达发射信号参数、电离层电子总量以及目标运动速度有关，当姿态角变化较小时，电离层电子总量可以视为取值固定的常数，在目标机动性不强时，目标上多个散射点运动可以用统一的速度和加速度来描述，空间目标在大多数情况下满足此条件。因此式（10） 可简化为

因此，目标回波可视为高阶相位系数相同的多分量多项式相位信号。

针对这类信号特点，可以先通过初成像得到目标ISAR图像，再从图像中分割出孤立散射中心，将其反变换到频域得到单散射中心回波信号，由式（11）可知，此时该散射中心回波信号可视为单分量多项式相位信号。单分量多项式相位信号可采用离散多项式变换算法［19］分别估计其二阶、三阶和四阶相位系数。假设估计得到的二阶、三阶和四阶相位系数分别为 aˆ2，aˆ3，aˆ4，则利用式（12）对该次回波进行高阶相位补偿。

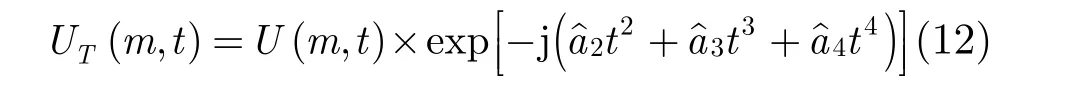
在DPT算法基础上，给出基于DPT的高阶相位补偿算法实现步骤为：

步骤 1 利用相关包络对齐和多普勒相位校正算法，对目标回波进行ISAR成像，得到初成像结果；

步骤 2 从初成像结果图中人工选择孤立散射中心，分割后通过逆傅里叶变换到频域，得到信号s（n）；

步骤 3 由信号 s（n），根据式（15），计算其四阶离散多项式变换，选择正整数 τ4，根据式（16）计算得到 aˆ4；

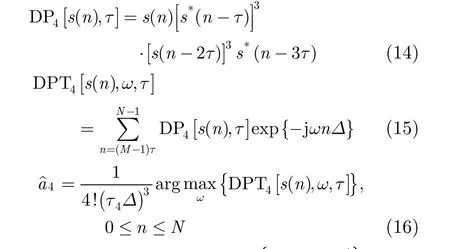
步骤 5 由信号 s2（n），根据式（18），计算其三阶离散多项式变换，选择正整数 τ3，根据式（19）计算得到；

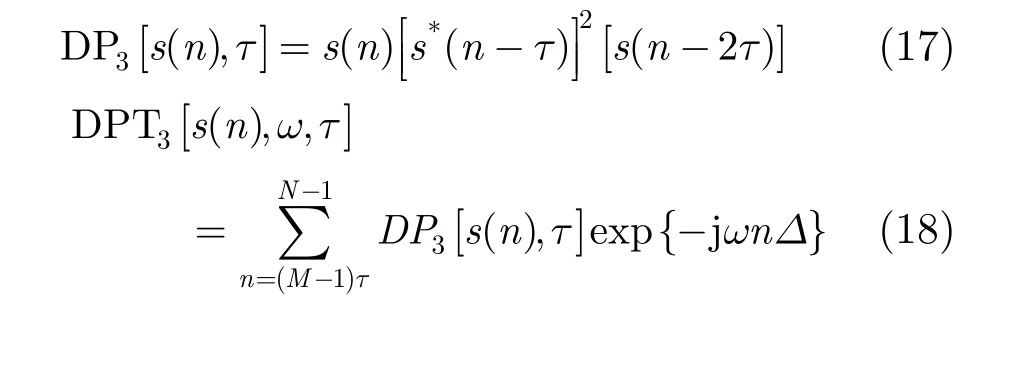
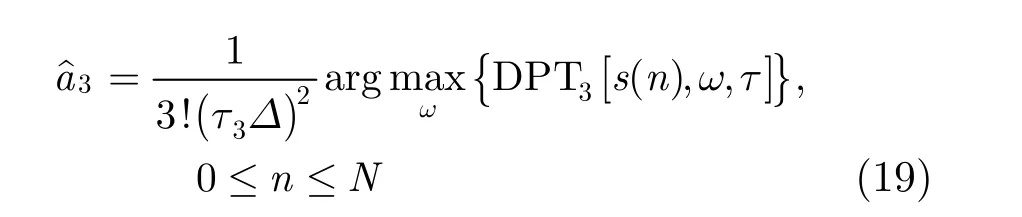
步骤 7 由信号 s3（n），根据式（21），计算其二阶离散多项式变换，选择正整数 τ2，根据式（22）计算得到 aˆ2；

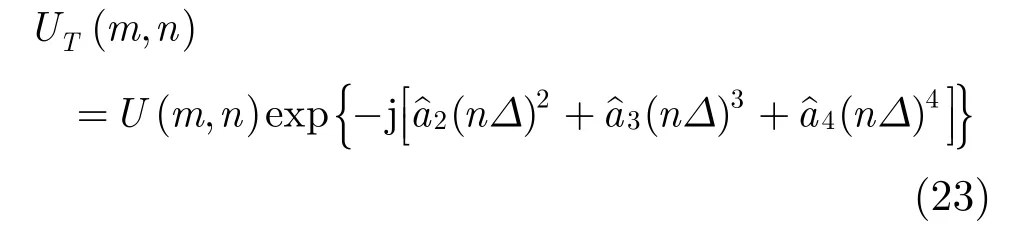
4 仿真实验

根据前面分析，在此进行了仿真实验。仿真的点目标模型分布如图1所示，各散射点的散射强度相同，间隔均为3 m。仿真时假设雷达发射信号为L波段线性调频信号：载频 fc= 2 GHz，带宽B=200 MHz，脉宽 T = 1 00μs ，脉冲重复频率 4 00 Hz，电离层电子总量 NT=1018el/m3，采样频率 fc=20 MHz，目标运动速度 V = 7 000 m/s ，加速度 a =6 m/s2。目标沿平行X轴的直线运动，如图2所示，成像积累角 θ = 6 .8°，目标回波按 5:1抽取，共取128个回波进行成像处理。

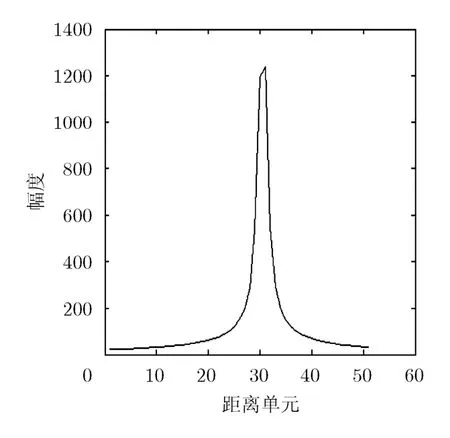
图3 单散射点1维距离像

图1 目标模型图

图2 目标ISAR 成像示意图

图3为目标只包含一个散射点时得到的1维距离像，图4为补偿后的1维距离像，可以看出经过高阶相位补偿后，距离像展宽效应可有效消除。

图5为对图1所示目标模型采用常规ISAR运动补偿和FFT进行成像处理的结果，图像模糊；图6为高阶相位补偿后目标ISAR成像处理的结果。可以看出，通过高阶相位补偿，可显著提高目标ISAR图像质量。

5 结论

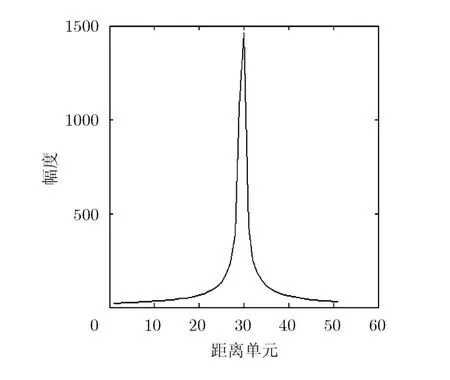
图4 补偿后的单散射点1维距离像

目标高速运动和电离层效应的存在都会对低频段宽带线性调频雷达信号产生较大影响，为得到正确的目标2维ISAR图像，需对此进行有效校正。本文通过对 L波段线性调频雷达信号进行数学建模，分析它们对成像分辨率的影响，在此基础上得到电离层高速运动目标回波信号模型，得出目标回波为高阶多项式相位信号的结论。结合目标回波特点给出了一种电离层高速运动目标ISAR成像自聚焦方法，该算法可准确估计高阶相位参数并进行有效补偿，提高了目标ISAR图像质量。该方法基于图像中孤立的散射中心，采用单分量多项式相位信号参数估计算法进行高阶相位参数估计。若图像中不存在孤立散射中心，则需采用多分量多项式相位信号的参数估计算法，这些是以后需要研究的。

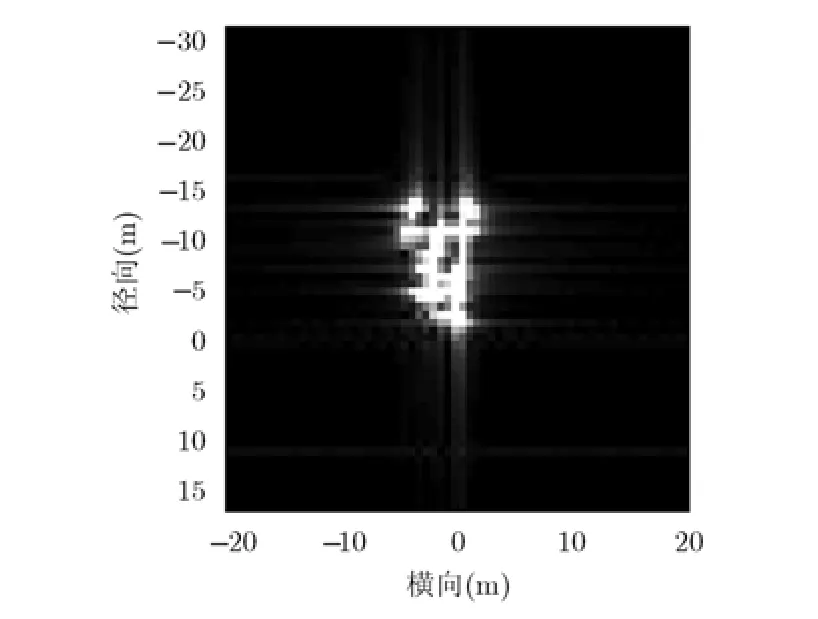
图5 补偿前目标ISAR像

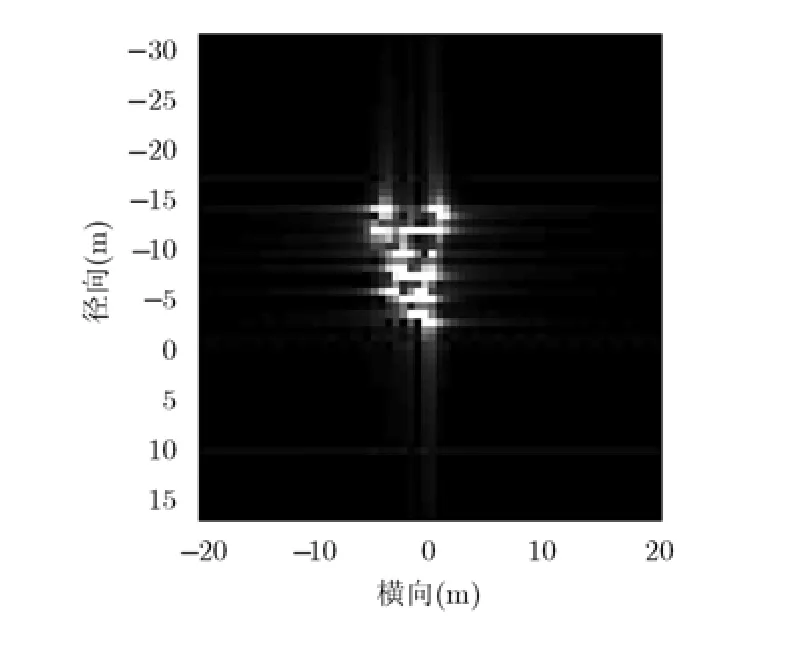
图6 补偿后目标ISAR像

［1］ 许志伟， 张磊， 邢孟道. 基于特征配准的ISAR图像方位定标方法［J］. 电子与信息学报， 2014， 36（9）: 2173-2179. Xu Zhi-wei， Zhang Lei， and Xing Meng-dao. A novel cross-rang scaling algorithm for ISAR images based on feature registration［J］. Journal of Electronics & Information Technology， 2014， 36（9）: 2173-2179.

［2］ 徐少坤， 刘记红， 袁翔宇， 等. 基于ISAR图像的中段目标二维几何特征反演方法［J］. 电子与信息学报， 2015， 37（2）: 339-345. Xu Shao-kun， Liu Ji-hong， Yuan Xiang-yu， et al.. Two dimensional geomtric feature inversion method for midcouse target based on ISAR image［J］. Journal of Electronics & Information Technology， 2015， 37（2）: 339-345.

［3］ 俞翔， 朱岱寅， 张劲东， 等. 基于设计结构化Gram矩阵的ISAR运动补偿方法［J］. 电子学报， 2014， 42（3）: 452-461. Yu Xiang， Zhu Dai-yin， Zhang Jing-dong， et al.. A motion compensation algorithm based on the designing structured gram matric［J］. Acta Electronica Sinica， 2014， 42（3）: 452-461.

［4］ Wang Y and Jiang Y C. Inverse synthetic aperture radar imaging of three-dimensional rotation target based on two-order match fourier transform［J］. IET Signal Processing，2012， 6（2）: 159-169.

［5］ Wang J F and Liu X Z. Improved global range alignment for ISAR［J］. IEEE Transactions on Aerospace and Electronic Systems， 2007， 43（3）: 1070-1075.

［6］ 刘波， 李道京， 李烈辰. 基于压缩感知的干涉逆合成孔径雷达成像研究［J］. 电波科学学报， 2014， 29（1）: 19-25. Liu Bo， Li Dao-jing， and Li Lie-chen. Moving target InSAR imaging and location based on compressed sensing［J］. Chinese Journal of Radio Science， 2014， 29（1）: 19-25.

［7］ 黄小红， 邱兆坤， 王伟. 目标高速运动对宽带一维距离像的影响及补偿方法研究［J］. 信号处理， 2002， 18（6）: 487-490. Huang Xiao-hong， Qiu Zhao-kun， and Wang Wei. Research on effect of wideband range profile imaging and compensating method for target moving with high velocity［J］. Signal Processing， 2002， 18（6）: 487-490.

［8］ Xing M D， Wu R B， and Bao Z. High resolution ISAR imaging of high speed moving targets［J］. IEE Proceedings-Radar， Sonar and Navigation， 2005， 152（2）: 58-67.

［9］ 刘红超， 纠博， 刘宏伟， 等. 一种匀加速空间目标高分辨距离像补偿算法［J］. 西安电子科技大学学报， 2012， 39（4）: 81-86. Liu Hong-chao， Jiu Bo， Liu Hong-wei， et al.. High resolution range profile compensation algorithm for the space target with uniform acceleration algorithm［J］. Journal of Xidian University， 2012， 39（4）: 81-86.

［10］ 唐辉， 胡卫东， 郁文贤. 电离层对L波段空间目标ISAR成像影响的建模与仿真［J］. 电波科学学报， 2007， 22（1）: 143-147. Tang Hui， Hu Wei-dong， and Yu Wen-xian. Modeling and simulation of ionospheric effects on L-band ISAR imaging of space objects［J］. Chinese Journal of Radio Science， 2007，22（1）: 143-147.

［11］ 李亮， 洪峻， 明峰， 等. 电离层时空变化对中高轨SAR成像质量的影响分析［J］. 电子与信息学报， 2014， 36（4）: 915-922. Li Liang， Hong Jun， Ming Feng， et al.. Study on ionospheric effects induced by spatio-temporal variability on mediumearth-orbit SAR imaging quality［J］. Journal of Electronics & Information Technology， 2014， 36（4）: 915-922.

［12］ Freeman A and Saatchi S S. On the detection of faradayrotation in linearly polarized L-band SAR backscatter signatures［J］. IEEE Transacions on Geoscience and Remote Sensing， 2004， 42（8）: 1607-1616.

［13］ Chen Jie， Li Zhou， Liu Wei， et al.. Image formation algorithm for topside ionosphere sounding with spaceborne HF-SAR system［C］. IEEE IGARSS Conference， Boston，Massachusetts， USA， 2008: II549-552.

［14］ 邢孟道， 保铮. 电离层电波传播相位污染校正［J］. 电波科学学报， 2002， 17（2）: 129-133. Xing Meng-dao and Bao Zheng. Phase perturbation correction in ionospheric electromagnetic wave propagation［J］. Chinese Journal of Radio Science， 2002， 17（2）: 129-133.

［15］ Nicoll J B and Meyer F J. Mapping the ionosphere using L-band SAR data［C］. IEEE IGARSS Conference， Boston，Massachusetts， USA， 2008: II537-540.

［16］ 赵宁， 周芳， 王振， 等. P 波段雷达成像电离层效应的地面观测与校正［J］. 雷达学报， 2014， 3（1）: 45-51. Zhao Ning， Zhou Fang， Wang Zhen， et al.. Ground observation and correction of P-band radar imaging ionospheric effects［J］. Journal of Radars， 2014， 3（1）: 45-51.

［17］ Peleg S and Friedlander B. Multicomponent signal analysis using the poloynomial-phase transform［J］. IEEE Transactions on Aerospace and Electronic Systems， 1996，32（1）: 378-386.

［18］ Barbarossa S， Scaglione A， and Georgios B G. Product high-order ambiguity function for multicomponent polynomial-phase signal modeling［J］. IEEE Transactions on Signal Processing， 1998， 46（3）: 691-708.

［19］ Peleg S and Friedlander Benjamin. The discrete polynomialphase transform［J］. IEEE Transactions on Signal Processing，1995， 43（8）: 1901-1914.

黄小红： 男，1975年生，副教授，研究方向为雷达成像和目标识别.

文贡坚： 男，1972年生，研究员，研究方向为目标识别.

Compensating Method of L-band Radar ISAR Imaging for Ionosphereic Target with High-velocity

Huang Xiao-hong Wen Gong-jian
（ATR Laboratory， National University of Defense Technology， Changsha 410073， China）

High velocity and Ionosphereic both modulate the phase of low carrier frequency wide-band linearly frequency modulated radar signal ， It make the resolution of Inverse SAR （ISAR） image lower. In order to get clean ISAR image， the effect of high velocity and ionosphereic are both must be removed. Firstly， signal model of ionosphereic target with high-velocity are deduced. The high order phase signal parameter estimation method is proposed， using discrete polynomial-phase transform. Motion compensation is done with the estimated values got by this method. Simulation experiments show that the parameters can be estimated right， it can improve the ISAR image deformed by hyper-velocity and ionosphereic.

Inverse SAR （ISAR）； Ionosphereic； Polynomial Phase Signal （PPS）； Motion compensation

The National Natural Science Foundation of China （61002025）

TN958

A

1009-5896（2015）12-2971-06

10.999/JEIT150646

2015-06-01；改回日期：2015-09-16；网络出版：2015-11-01

*通信作者：黄小红 atrhuang@126.com

国家自然科学基金（61002025）