利用视觉目标遮挡和轮廓信息确定下一最佳观测方位

张世辉韩德伟何 欢（燕山大学信息科学与工程学院 秦皇岛 066004）

②（河北省计算机虚拟技术与系统集成重点实验室 秦皇岛 066004）

利用视觉目标遮挡和轮廓信息确定下一最佳观测方位

张世辉*①②韩德伟①何 欢①①（燕山大学信息科学与工程学院 秦皇岛 066004）

②（河北省计算机虚拟技术与系统集成重点实验室 秦皇岛 066004）

下一最佳观测方位的确定是视觉领域一个比较困难的问题。该文提出一种基于视觉目标深度图像利用遮挡和轮廓信息确定下一最佳观测方位的方法。该方法首先对当前观测方位下获取的视觉目标深度图像进行遮挡检测。其次根据深度图像遮挡检测结果和视觉目标轮廓构建未知区域，并采用类三角剖分方式对各未知区域进行建模。然后根据建模所得的各小三角形的中点、法向量、面积等信息构造目标函数。最后通过对目标函数的优化求解得到下一最佳观测方位。实验结果表明所提方法可行且有效。

深度图像；遮挡；轮廓；未知区域；类三角剖分；下一最佳观测方位

1 引言

下一最佳观测方位（Next Best View， NBV）的确定是指根据摄像机（传感器）在当前观测方位下获取到的视觉目标信息确定出摄像机的下一观测方位，使得摄像机在所求方位下能够最大量地获取到当前观测方位下未采集到的信息。下一最佳观测方位的确定一直是数据采集、3维重建、机器人导航、自动装配、目标识别等领域重要且困难的研究课题之一，受到学者们的广泛关注［1-4］。

目前，下一最佳观测方位确定算法所基于的图像信息类型主要有两种：图像亮度信息［5，6］和图像深度信息［7-11］。同亮度图像相比，深度图像更利于获得场景的3维信息，因此，现有的下一最佳观测方位确定算法通常都基于深度图像实现。文献［7］采用八叉树模型描述视觉目标，并根据每个节点的实际情况对其进行标记，进而确定下一最佳观测方位。该方法是求解下一最佳观测方位问题方面最早的方法，但该方法由于未考虑遮挡因素，故当视觉目标出现遮挡现象时，无法保证所得结果的正确性和有效性。文献［8］通过对视觉目标遮挡区域进行多边形建模，利用遮挡信息确定下一最佳观测方位，但该方法需要特定的设备，适用范围有限。文献［9］提出一种基于整体观测策略确定下一最佳观测方位的方法，该方法要求对视觉目标有一定的了解且该方法确定出的摄像机位置被限定在一个固定的表面，方法的通用性受到了限制。文献［10］提出一种基于 B样条计算信息熵的视点规划方法，该方法将摄像机获得模型最大信息熵的方位作为下一最佳观测方位，但该方法没有充分利用视觉目标背面的信息，并且计算出的摄像机位置同样被限定在一个固定的表面。文献［11］提出了一种基于射线追踪的下一最佳观测方位确定方法，该方法的思想是从若干候选观测方位中确定出下一最佳观测方位，导致所求结果被限定在事先确定的候选观测方位中。文献［12］利用当前观测方位下未观测到区域的置信模型来估计每个可能的观测点的信息增益，提出一种灵活的概率框架来估计下一最佳观测方位，但该方法涉及到的可观测性参数需要人为设定。

针对已有方法存在的未考虑遮挡因素、摄像机位置受限等方面的不足，本文提出一种基于深度图像利用遮挡和轮廓信息确定下一最佳观测方位的方法。

2 方法概述

2.1相关概念

当摄像机观测视觉目标时，视觉目标的一部分表面会遮挡另外一部分表面。遮挡边界是当前观测方位下视觉目标上遮挡部分与被遮挡部分的分界线，该分界线由遮挡部分的像素点组成，且每个遮挡边界点都在各自的八邻域点内对应一个深度差最大点，这个深度差最大点称为该遮挡边界点的下邻接边界点，下邻接边界点组合形成下邻接边界。图1为深度摄像机观测视觉目标并获取视觉目标深度图像的示意图。其中，红色线表示当前观测方位下获取到的视觉目标的轮廓，黄色线表示遮挡边界，蓝色线表示下邻接边界。

分析图1可知，本文把由遮挡边界及其对应的下邻接边界组成的区域及当前观测方位下获取到的视觉目标轮廓所围成的视觉目标的背面区域统称为未知区域。对未知区域的观测可以得到视觉目标更多的信息。为了获取视觉目标更多的信息，需要对视觉目标进行下一次观测。在所有下一观测方位中能够最多地获取到视觉目标未知信息的观测方位称为下一最佳观测方位。

2.2 总体思想

本文方法总体思想如下。首先，获取视觉目标的一幅深度图像，同时记录下摄像机的内外参数；其次，根据深度图像中的遮挡和轮廓信息构建未知区域；再次，对未知区域进行类三角剖分建模，并计算出各小三角形的中点、法向量和面积；然后，基于所有小三角形信息构造出以摄像机位置为自变量，以该观测方位下可以被实际观测到的小三角形面积为因变量的函数，将下一最佳观测方位求解问题转化为函数优化问题；最后，通过优化算法求解目标函数确定出下一最佳观测方位。

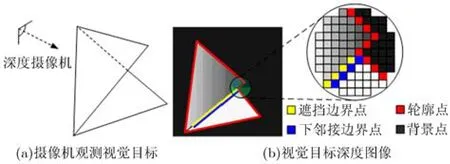
图1 摄像机观测并获取视觉目标深度图像示意图

3 下一最佳观测方位确定方法

3.1 构建未知区域并计算各未知区域的中点

首先利用文献［13］中的遮挡边界检测方法检测出深度图像中的遮挡边界，然后把每条遮挡边界与其对应的下邻接边界组成一个未知区域。此外，通过分析深度图像中的像素点可知，八邻域点内有且不全为背景点或数据点的数据点为轮廓点，根据轮廓点的这个特征提取出视觉目标的轮廓。

本文定义未知区域的中点为围成该区域的所有像素点的3维中心点，即未知区域中点的计算公式为

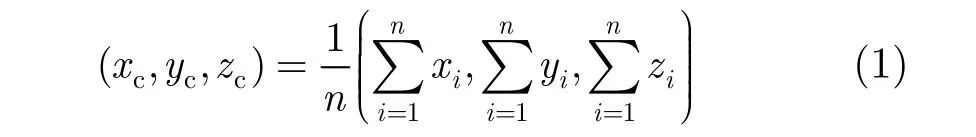
3.2 未知区域建模

为了实现对遮挡边界产生的未知区域的建模，还需确定出未知区域对应的遮挡边界的端点。通过分析深度图像中遮挡边界点之间的位置关系可知，如果遮挡边界点P'的八邻域内只有一个遮挡边界点或只有两个相邻的遮挡边界点，那么遮挡边界点P'一定为该遮挡边界的端点。除以上两种情况外遮挡边界点P'均不为端点。判断遮挡边界点P'的八邻域内的两个遮挡边界点是否相邻的公式为

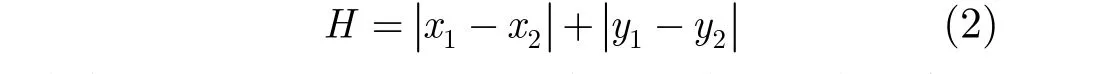
图2展示了某一未知区域按上述方法建模后的效果。其中，黄色点代表遮挡边界上的遮挡边界点，蓝色点代表与之对应的下邻接边界点，绿色点代表该区域的中点。

3.3 计算小三角形的中点、法向量和面积

未知区域建模后为了求解下一最佳观测方位，需要确定各小三角形的中点、法向量和面积。小三角形的中点为构成小三角形的3个顶点的3维中心点，计算公式为

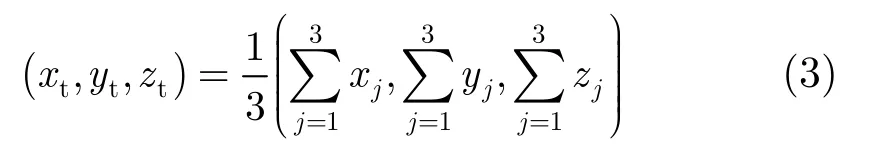
下面以图3所示的某一未知区域中的一个小三角形ABC为例说明小三角形法向量的计算方法。

图3中A， B为相邻的遮挡边界点或下邻接边界点，C为该未知区域的中点，T为小三角形的中点。构成小三角形的3个顶点的3维坐标两两相减可以得到6个共面的向量。根据向量叉乘的定义可以推出，上述6个向量中任意两个不共线向量的叉积即为小三角形的法向量。为了保证计算出的小三角形实际可观测面积的有效性，本文选取指向视觉目标外部的法向量作为小三角形的法向量。下面以6个向量中点A到点B的向量a和点A到点C的向量c为例详细介绍小三角形法向量的计算方式。

为了得到指向视觉目标外部的法向量就要确定两个向量的叉乘顺序，即 a ×c还是 c ×a。下面以为例给出其计算公式：

式中，i， j， k分别为直角坐标系下与坐标轴相对应的3个单位向量分别为向量a和c的坐标表示。通过分析遮挡边界和下邻接边界的性质可知：由位置关系不同的遮挡边界与其下邻接边界所围成的未知区域内的小三角形的法向量计算方式是不同的，但同一个区域内的小三角形的法向量的计算方式是相同的。确定两个向量的叉乘顺序的方法描述如下：

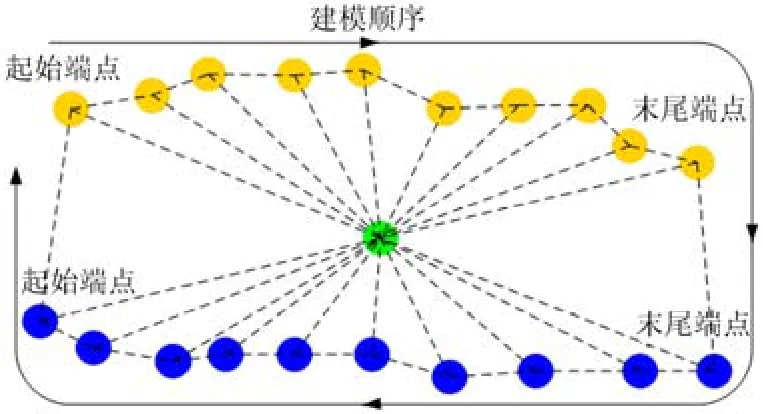
图2 未知区域建模示意图

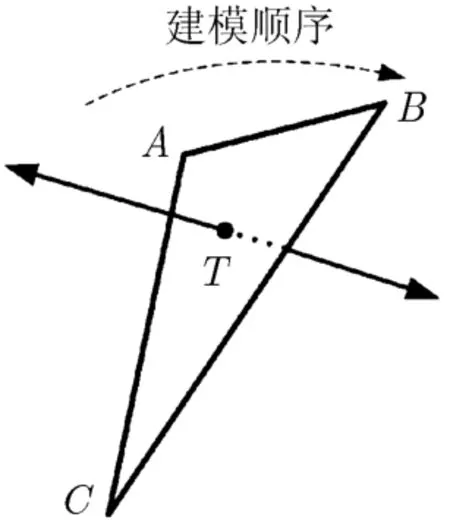
图3 小三角形的中点及其法向量示意图

由图4可以看出，为了保证所求得的小三角形法向量指向视觉目标的外部，图4（a）， 4（b）， 4（c）， 4（d）4种情形下对应的小三角形法向量的计算方式应为点A'到点B'的向量叉乘上点A'到点C'的向量，对应为 a ×c。图4（e）， 4（f）， 4（g）， 4（h）4种情形下对应的小三角形法向量的计算方式应为点A'到点 C'的向量叉乘上点A'到点B'的向量，对应为 c ×a。因此判断某一未知区域内小三角形法向量的计算方式问题就可转换成判断该未知区域属于图4中哪种情形的问题。

然后，出于在一条遮挡边界的两个端点横坐标相等时斜率k依然有意义以及简化计算的考虑，根据上述分析把斜率k的计算方式改进为

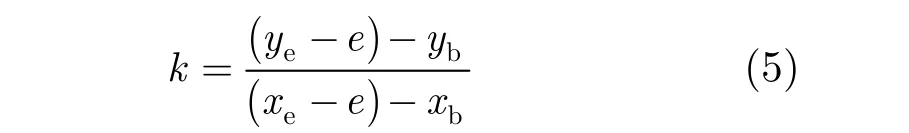
式中，e为一个大于 0的小数。考虑到极端情况，也就是当一条遮挡边界只有两个像素点组成时，如果e大于或等于 0.5就有可能造成遮挡边界与其下邻接边界的位置关系的误判，因此本文限定0 ＜ e＜ 0.5。这样就可以把情形图4（a）， 4（c）， 4（e），4（g）分别归并到情形图4（b）， 4（d）， 4（f）， 4（h）。点与直线位置关系的确定公式为

最后，通过判断某一未知区域计算出的k和D的值来确定该未知区域内的小三角形法向量的计算方式。也就是说，当 k＜ 0且 D＞ 0时，即情形图4（b），对应的法向量的计算方式为 a ×c；当 k＞ 0且D＜ 0时，即情形图 4（d），对应的法向量的计算方式为 a ×c；当 k＜ 0且 D＜ 0时，即情形图4（f），对应的法向量的计算方式为 c ×a；当 k＞ 0且 D＞0时，即情形图 4（h），对应的法向量的计算方式为c ×a。考虑到轮廓点所围成的未知区域只有一种情形且比较简单，又由于轮廓所代表的未知区域为视觉目标的背面，为了得到指向视觉目标外部的法向量，计算该区域内的小三角形的法向量时两个向量的叉乘顺序应为 a ×c。

图4 遮挡边界与其下邻接边界的位置关系示意图

得到小三角形的法向量后就可以求出小三角形的面积。第i个小三角形的面积 si的计算公式为

3.4 下一最佳观测方位问题转化

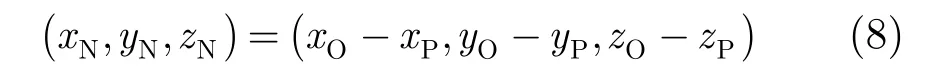
由此可见只要计算出摄像机位置即可完成对下一最佳观测方位问题的求解。基于上述分析，求解下一最佳观测方位下摄像机位置的公式为

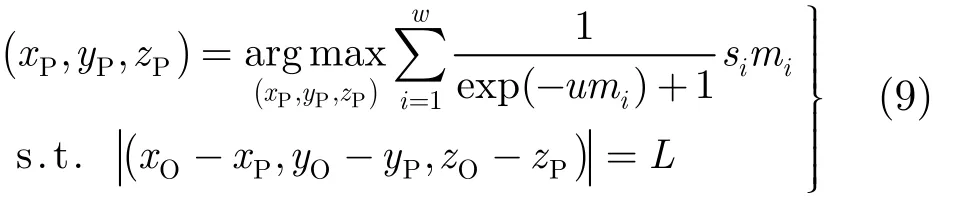
式中，w为所有小三角形的个数，u为常数，u值越大函数越精确，但考虑到时空开销，经多组实验对比，本文选取 u= 300。 si为第i个小三角形的面积。 mi为第i个小三角形的法向量与向量夹角的余弦值。是一个激活函数：当 mi为正时，约等于1，即小三角形能被摄像机观测到时小三角形参与计算，此时 mi与面积 si的乘积表示小三角形实际被摄像机观测到的面积；当 mi为负时，约等于0，表示小三角形不能被摄像机观测到，此时小三角形不参与计算。L为当前观测方位下摄像机的观测距离。

经上述处理后，下一最佳观测方位求解问题就转化为式（9）的函数优化问题，通过对函数的优化求解即可得出下一最佳观测方位。

3.5 下一最佳观测方位函数优化求解

根据3.4节的描述可知，式（9）的最优解即为下一最佳观测方位下摄像机的位置。由于物体的全局几何信息是未知的，所以本文要解决的是一个非凸问题，即式（9）是一个非凸函数。本文采用一种当前公认的处理中小规模非线性规划问题的最好算法中的序列二次规划［14］算法对式（9）进行求解。

本文方法根据摄像机在当前观测方位下获取到的视觉目标的轮廓及遮挡情况的不同利用式（10）计算得出初始迭代位置。通过分析小三角形的位置、大小和法向量定义初始迭代位置为

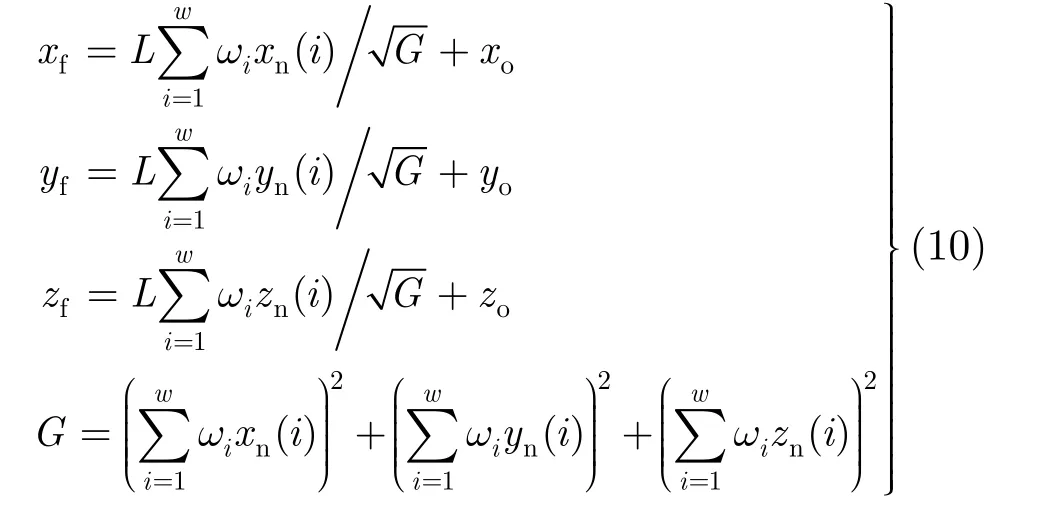
4 实验及分析

4.1 实验方案和数据集

为了验证所提方法的可行性和有效性，本文做了3组实验：（1）所提方法各阶段结果的可视化实验；（2）不同方法计算摄像机观测点时对最终结果影响的对比实验；（3）不同下一最佳观测方位确定方法之间的对比实验。实验硬件环境为 Intel（R）Core（TM）2 Duo CPU E7500、内存2.0 G。算法采用C++编程实现。实验分为仿真实验和真实实验，仿真实验所用 Bunny， Duck， Dragon， Mole和Rocker 3维模型来自深度图像领域较著名的Stuttgart Range Image Database［15］，真实实验所用Bonsai， Box和Kettle是现实生活中的3个实物。仿真实验中，通过OpenGL模拟摄像机观测3维模型并获取其深度图像，设置投影矩阵的参数为（60，1，200，600），摄像机观测距离为 300 mm。真实实验中，用Kinect相机采集深度图像，设定摄像机观测距离为1.2 m，其余设置与仿真实验一致。

4.2 实验结果及分析

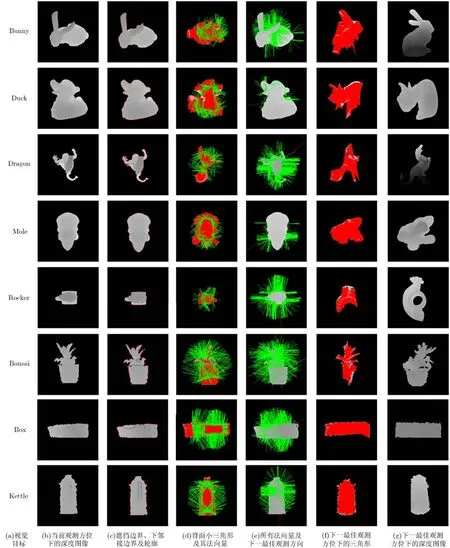
图5 本文方法各阶段结果的可视化图

4.2.1 所提方法的可视化实验为了更加形象地说明本文方法的求解过程，图5给出了本文方法各阶段结果的可视化图。

由图5展示的实验结果可以看出，对于遮挡情况不太显著的Duck和Kettle而言，由于其轮廓所围成的未知区域内小三角形的面积在建模所得总的小三角形的面积中所占比重较大，故所求下一最佳观测方位更加偏向于直接观测视觉目标的背面；对于遮挡情况相对显著的 Bunny， Dragon， Mole，Rocker， Bonsai和Box而言，由于其由遮挡边界及下邻接边界建模所得三角形的面积在建模所得总的小三角形的面积中也占有较大比重，故这6个视觉目标所求下一最佳观测方位兼顾遮挡和轮廓信息。由此可见，基于视觉目标遮挡及轮廓进行建模，并利用建模所得三角形信息进行下一最佳观测方位的求解方案是可行的，且无论是数据集中的模型还是现实生活中的实物，本文方法所求下一最佳观测方位都与人类视觉的观测习惯相符。

4.2.2 不同观测点计算方法对下一最佳观测方位影响的对比实验

摄像机观测点的选取将对最终计算出的下一最佳观测方位下获取的信息产生较大的影响。为了验证本文摄像机观测点计算方法的有效性。我们对基于两种不同的观测点计算方法的实验结果进行了比较。第1种为本文3.4节所提的摄像机观测点计算方法，在此不再赘述。第2种摄像机观测点的计算方法为

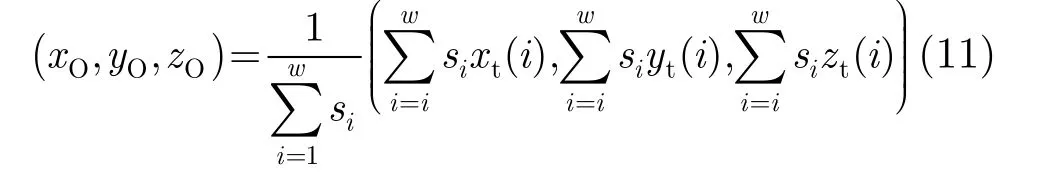
式（11）表明该计算方法下摄像机观测点为以各小三角形面积为权重的小三角形中点坐标的平均值。

表1给出了摄像机在两种不同观测点计算方法所求解出的下一最佳观测方位下获取的视觉目标表面点的量化结果。其中 Nn代表摄像机在下一最佳观测方位下获取到的视觉目标表面点的个数， No代表被重复观测到的视觉目标表面点的个数， Nnew表示实际新增点的个数。由表1中可以看出，采用本文所提第1种观测点计算方法时的结果明显优于采用第2种观测点计算方法时的结果。

4.2.3 不同下一最佳观测方位方法间的对比实验

为了更好地评估本文方法的效果，我们将本文方法与同样基于深度图像且考虑了遮挡信息的文献［9］，文献［10］中的方法做了对比实验。图6给出了部分具有代表性的视觉目标在不同下一最佳观测方位求解方法下对应的实验结果。

由图6可以看出，文献［9］方法计算出的下一最佳观测方位侧重观测当前观测方位下视觉目标的背面。文献［10］方法计算出的下一最佳观测方位侧重观测当前观测方位下信息增益较大点的相邻未知区域。本文方法通过充分利用遮挡、轮廓的信息，计算出了一个更加合理的下一观测方位。

为了进一步衡量不同方法的性能，我们对不同方法的结果进行了量化评估。表2给出了不同方法所求下一最佳观测方位下的 Nn，No，Nnew，重合率和新增率 Rnew。

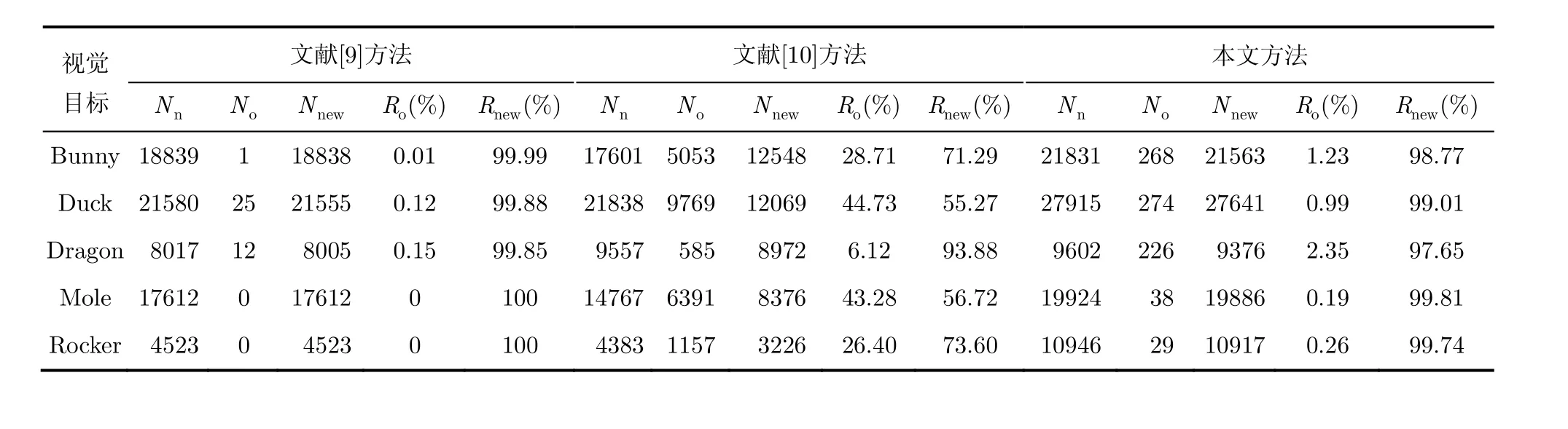
表2 不同方法在所求下一最佳观测方位下实验结果的量化评估

分析表2可知，就文献［9］方法而言，因为其主要观测当前观测方位下视觉目标的背面，因此在其所求得的下一最佳观测方位下获得的表面点重合率较低，新增点个数与当前观测方位下获取到的图像中视觉目标轮廓的大小有直接关系。例如 Bunny，Duck和Mole，因为在当前观测方位下获取的视觉目标的轮廓相对较大，所以其获得的新增点数较多；而对于Dragon和Rocker，因为在当前观测方位下获取的视觉目标的轮廓相对较小，所以其获得的新增点数较少。由此可见，文献［9］方法具有较大的局限性。就文献［10］方法而言，其根据已观测点中信息增益较大点及其法向量计算下一最佳观测方位。该方法求得的最佳观测这些已观测信息增益较大点的观测方位即为下一最佳观测方位，这就导致了该方法求得的下一最佳观测方位与当前观测方位之间的角度相差不大，因此在该所求观测方位下获取到的表面点与当前观测方位下获取到的表面点重合率较高，新增点个数相对较少。对于某些特殊的视觉目标例如 Dragon而言，因为其表面比较复杂，所以重合率相对较低。而对于其他视觉目标而言，其重合率都较高。本文方法通过建立综合考虑视觉目标遮挡及轮廓信息的求解模型，采用优化算法对模型求解获得下一最佳观测方位。由表2的量化评估结果可以看出，在最能反映方法效果的新增点个数指标上，本文方法结果明显优于文献［9］和文献［10］方法的结果，更好地达到了下一最佳观测方位问题的求解要求。

综合图6和表2的结果可知，在相同的实验条件（如观测距离）下，本文方法较其他方法获得的下一最佳观测方位更为合理。

5 结束语

本文提出一种基于深度图像利用遮挡和轮廓信息求解下一最佳观测方位的方法。该方法无需限定摄像机的观测位置，具有较好的通用性。所提方法的贡献在于：（1）提出一种综合考虑遮挡和物体轮廓信息的视觉目标未知区域建模方法，使得计算出的下一最佳观测方位更加合理，克服了只利用遮挡或视觉目标背面信息求解下一最佳观测方位方法的局限性；（2）根据建模所得小三角形的中点、法向量和面积等信息构造了目标函数，使下一最佳观测方位确定问题转化为优化问题；（3）给出一种根据当前观测方位下所获得的视觉目标信息确定优化函数初始迭代位置的计算方法，该计算方法对视觉目标具有自适应性，有助于获得较好的下一最佳观测方位求解结果。

图6 不同方法在所求下一最佳观测方位下的视觉目标深度图像

［1］ Bottino A and Laurentini A. What is next an interactive next best view approach［J］. Pattern Recognition， 2006， 39（1）: 126-132.

［2］ Pintilie G D and Stuerzlinger W. An evaluation of interactive and automated next best view methods in 3D scanning［J］. Computer-Aided Design and Applications， 2013， 10（2）: 279-291.

［3］ 曾明勇， 吴泽民， 田畅， 等. 基于外观统计特征融合的人体目标再识别［J］. 电子与信息学报， 2014， 36（8）: 1844-1851. Zeng Ming-yong， Wu Ze-min， Tian Chang， et al.. Fusing appearance statistical features for person re-identification［J］. Journal of Electronics & Information Technology， 2014， 36（8）: 1844-1851.

［4］ 李烈辰， 李道京. 基于压缩感知的连续场景稀疏阵列 SAR三维成像［J］. 电子与信息学报， 2014， 36（9）: 2166-2172. Li Lie-Chen and Li Dao-jing. Sparse array SAR 3D imaging for continuous scene based on compressed sensing［J］. Journal of Electronics & Information Technology， 2014， 36（9）: 2166-2172.

［5］ Trummer M， Munkelt C， and Denzler J. Online next-best-view planning for accuracy optimization using an extended E-criterion［C］. Proceedings of the 20th International Conference on Pattern Recognition， Istanbul，Turkey， 2010: 1642-1645.

［6］ Haner S and Heyden A. Covariance propagation and next best view planning for 3D reconstruction［C］. Proceedings of the 12th European Conference on Computer Vision， Florence，Italy， 2012: 545-556.

［7］ Connolly C. The determination of next best views［C］. Proceedings of the IEEE International Conference on Robotics and Automation， Missouri， USA， 1985: 432-435.

［8］ Maver J and Bajcsy R. Occlusion as a guide for planning the next view［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1993， 15（5）: 417-432.

［9］ Banta J E， Wong L M， Dumont C， et al.. A next-best-view system for autonomous 3-D object reconstruction［J］. IEEE Transactions on Systems， Man， and Cybernetics， Part A: Systems and Humans， 2000， 30（5）: 589-598.

［10］ Li Y F and Liu Z G. Information entropy-based viewpoint planning for 3-D object reconstruction［J］. IEEE Transactions on Robotics， 2005， 21（3）: 324-337.

［11］ Vasquez-Gomez J I， Sucar L E， and Murrieta-Cid R. Hierarchical ray tracing for fast volumetric next-best-view planning［C］. Proceedings of the International Conference on Computer and Robot Vision， Regina， SK， Canada， 2013: 181-187.

［12］ Potthast C and Sukhatme G. A probabilistic framework for next best view estimation in a cluttered environment［J］. Journal of Visual Communication and Image Representation，2014， 25（1）: 148-164.

［13］ 张世辉， 刘建新， 孔令富. 基于深度图像利用随机森林实现遮挡检测［J］. 光学学报， 2014， 34（9）: 0915003: 1-12. Zhang Shi-hui， Liu Jian-xin， and Kong Ling-fu. Using random forest for occlusion detection based on depth image［J］. Acta Optica Sinica， 2014， 34（9）: 0915003: 1-12.

［14］ Curtis F and Overton M. A sequential quadratic programming algorithm for nonconvex， nonsmooth constrained optimization［J］. SIAM Journal on Optimization，2012， 22（2）: 474-500.

［15］ Hetzel G， Leibe B， Levi P， et al.. 3D object recognition from range images using local feature histograms［C］. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition， Piscataway， USA， 2001: II394-II399.

张世辉： 男，1973 年生，博士，教授，博士生导师，研究方向为视觉信息处理、模式识别.

韩德伟： 男，1989 年生，硕士生，研究方向为遮挡检测与规避.

何 欢： 男，1989 年生，硕士生，研究方向为计算机视觉.

Determining Next Best View Using Occlusion and Contour Information of Visual Object

Zhang Shi-hui①②Han De-wei①He Huan①
①（School of Information Science and Engineering， Yanshan University， Qinhuangdao 066004， China）②（The Key Laboratory for Computer Virtual Technology and System Integration of Hebei Province，Qinhuangdao 066004， China）

Determining camera’s next best view is a difficult issue in visual field. A next best view approach based on depth image of visual object is proposed by using occlusion and contour information in this paper. Firstly， the occlusion detection is accomplished for the depth image of visual object in current view. Secondly， the unknown regions are constructed according to the occlusion detection result of the depth image and the contour of the visual object， and then the unknown regions are modeled with triangulation-like. Thirdly， the midpoint， normal vector and area of each small triangle and other information are utilized to establish the objective function. Finally， the next best view is obtained by optimizing objective function. Experimental results demonstrate that the approach is feasible and effective.

Depth image； Occlusion； Contour； Unknown regions； Triangulation-like； Next best view

s: The National Natural Science Foundation of China （61379065）； The Natural Science Foundation of Hebei Province （F2014203119）

TP391

A

1009-5896（2015）12-2921-08

10.11999/JEIT150190

2015-02-02；改回日期：2015-08-19；网络出版：2015-11-01

*通信作者：张世辉 sshhzz@ysu.edu.cn

国家自然科学基金（61379065）和河北省自然科学基金（F2014203119）