带虚警抑制的基于归一化残差的野值检测方法
汝小虎柳 征 姜文利 黄知涛
(国防科学技术大学电子科学与工程学院 长沙 410073)
带虚警抑制的基于归一化残差的野值检测方法
汝小虎*柳 征 姜文利 黄知涛
(国防科学技术大学电子科学与工程学院 长沙 410073)
野值检测,或称异常值检测是模式识别和知识发现中一个重要的问题。以往的野值检测方法难以有效地抑制虚警概率,针对这一问题,该文提出一种带监督情形下基于归一化残差(Normalized Residual, NR)的野值检测方法。首先利用训练样本计算待考查模式的NR值,其次比较NR值与野值检测门限的相对大小,从而判断待考查模式是否为野值。该文理论上推导了野值门限与虚警概率之间的关系表达式,以此为依据设置检测门限,可实现在少量训练样本情况下仍能抑制虚警率的目的。计算机仿真和实测数据测试验证了所提方法在野值检测和虚警抑制方面的优越性能。
模式识别;监督;野值检测;虚警概率;归一化残差
1 引言
野值定义为这样的样本,它偏离其他模式太远以至于可认为它是由不同机制产生的[1]。野值检测被广泛应用于模式识别,知识发现和数据挖掘中,具体的问题如视频监控,计算机入侵检测,特定辐射源确认(Specific Emitter Verification, SEV)[2],混合标记数据集中的稳健分类[3]以及粒子图像测速(Particle Image Velocimetry, PIV)数据中的奇异值检测[4,5]等。
不同的应用背景一般会有不同的野值检测技术[6-8],而以野值检测方法的种类进行区分,可主要分为基于概率分布的[3],基于深度的[9],基于距离的[10-14],基于密度的[15]和基于聚类的[16-18]方法;以是否利用训练样本进行区分,可分为带监督的和无监督的方法。针对带监督的野值检测问题,文献[16]提出了基于单类支持向量机(Support Vector Machine, SVM)的野值检测方法,该方法将样本映射到高维核空间,利用训练样本建立超平面决策界,测试时把位于界外的样本判为野值。文献[17]引入动态学习的思想,实现了训练样本较少情况下超平面界的迭代扩张。文献[18]扩展了单类SVM,对多类情形实现了稳健分类和野值检测。但是这些方法存在一个共同的不足,即无法控制虚警概率。文献[12-14]提出了局部化 p值估计(Localized P-value Estimation, LPE)的方法,该方法利用训练样本计算某种统计量G,通过比较考查模式和训练样本G值的相对大小得到p值的估计,如果p值大于指定的虚警率水平则将考查模式判为野值。若训练样本足够并且野值满足均匀分布假设,LPE方法可控制虚警率,同时实现一致最大势(Uniformly Most Powerful, UMP)检验,但是当训练样本较少时该方法仍然难以抑制虚警率。文献[4,5,10]提出了基于归一化残差(Normalized Residual, NR)的野值检测方法。待考查模式的残差定义为该模式与其近邻模式间的距离,这一距离与近邻模式内部距离的比值称为模式的NR值。如果该值大于预先设定的野值门限则将待考查模式判为野值,否则认为其为正常模式。野值门限大小的设置往往依赖于经验,虽然选择较大的门限可以降低虚警率,但是其具体的对应关系仍然未见报道。
针对前述文献中方法存在的不足,本文将以往基于NR的野值检测转化为带监督的情形,提出一种能有效抑制虚警概率的野值检测方法。为便于理论分析,在计算待考查模式的NR值方面,本文用随机选择的部分训练样本代替近邻模式作为计算的依据。在野值检测门限设置方面,本文根据重新定义的 NR,从理论上推导野值门限与虚警率之间的关系表达式,以此为依据设置门限的大小。此外,为了使检测方法更加稳健,本文多次从训练样本中随机选择部分样本,计算得到多个NR值,之后将这些值的平均与野值门限进行比较,由此判断出待考查模式是否为野值。仿真实验和实测数据测试发现,本文方法在较少训练样本情况下能够更好地抑制虚警率,并且达到较高的野值检测概率,性能优于同类方法。
本文剩余部分安排如下:第2节简单介绍典型的LPE方法,作为同类方法,它会被用于和本文方法进行性能比较;第3节提出基于NR的野值检测方法,包括NR的定义、野值检测门限的理论推导以及具体的方法步骤;第4节通过仿真和实测数据测试验证本文方法的优良性能;最后总结全文。
2 LPE方法[12-14]
文献[12-14]将野值检测转化为二元假设检验问题,两种假设分别为 H0:η ~f0和 H1:η ~f1,其中f1是区别于 f0的概率密度函数。带有虚警抑制的野值检测要求概率 P {判 为 H1|H0}≤α,其中α是指定的显著水平。定义考查模式η的p值函数为

并假设 f1是均匀分布,那么该二元假设检验问题的UMP检验是

由于 f0未知,所以直接计算式(1)是不可能的。文献[12-14]基于某种统计量G,定义

其中I是指示函数,通过 ˆp(η)实现对 p(η)的近似,并证明了这种近似是渐进无偏的。
文献[12]将统计量G定义为 G (x )= D(K)(x),即x与它周围训练样本第K个最近的距离,因此被称为 K-LPE方法。文献[13]定义了新的统计量 G(x),其中表示向下取整,并在计算 G时采用平均的思想,提出了平均 K-LPE(averaged K-LPE,aK-LPE)方法。其基本思路是将训练样本随机平分为两部分,其中一部分的样本 xi作为考查模式时,需从另一部分的样本中寻找其近邻样本,计算得到G值。上述过程重复B次,将得到的所有G值取平均作为最后的统计量结果 G(xi)。 G(η)的计算需要首先随机选定一半训练样本,从中选择η的K个近邻样本,然后通过类似计算 G(xi)的过程得到。文献[14]则实现了LPE野值检测方法速度上的优化。
在训练样本足够的情况下,式(3)中 ˆp(η)对 p(η)会有较好的近似,但是近似效果会随着训练样本数的减小而变差,这限制了LPE方法的应用。
3 基于归一化残差的方法
3.1 归一化残差的定义
以往对归一化残差(NR)的计算[4,5,10]用于解决无监督的野值检测问题,对于带监督的情形,本文在文献[10]的基础上对NR进行重新定义。从训练样本集 Xtr中随机选择K个样本,k = 1,2,…, K ,那么待考查模式η的NR值可由式(4)计算得到。

在进行野值检测时,需要设置门限h,如果r > h则认为η为野值,否则认为 η ~f0为正常模式。以往的研究中对h的选择带有很大的主观性,一般依据经验设置为1~4。本文考虑对虚警率的控制,因此需要对门限的设置进行理论推算,将其表示为虚警率的函数。为便于分析,本文取消加权因子即设认为所有随机选择的训练样本对于判别η是否为野值具有同等的重要性。
3.2 野值门限的确定
野值门限的大小与所需的虚警率有关,所以只要分析待考查模式为正常模式的情形即可,即如果正常模式被识别为野值,则产生虚警。首先考虑高斯白噪声的情况。设K个随机选择的训练样本为待考查模式为 η= xk=其中 x0是模式的理论值,模式噪声满足为噪声方差。
根据定义,忽略容差ξ的影响,正常模式 xk的归一化残差其中


其中E{·}表示计算期望。
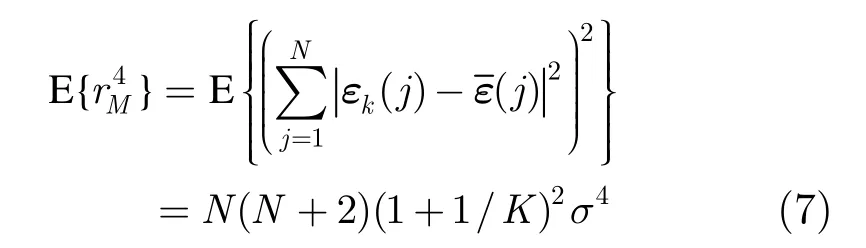
由式(6)和式(7)可得r分子平方的方差为

下面计算r分母平方的均值与方差。利用


由式(8)和式(10), r2的分子与分母方差的比值为一般这是个远大于1的数。所以r2的分母相对其分子而言较为稳定,可将视为常量,其大小为

联合式(6),式(8),式(11),可得到正常模式NR值平方的均值和方差:

另外,容易证得 r2服从高斯分布。设野值检测门限为 h≥ 0,利用r和h的非负性,可得本文基于NR的野值检测方法的虚警概率为

其中 Q{·}是标准高斯分布N(0,1)的右尾概率。
设所需的虚警概率为 α= Pf,根据式(14),可得到本文方法在进行野值检测时应设置的检测门限大小为

现在考虑色噪声情形。假设噪声的均值为零,可设 εi~N( 0, C),其中C是噪声的协方差矩阵,满足表示共轭转置。假设C是已知的,或者通过
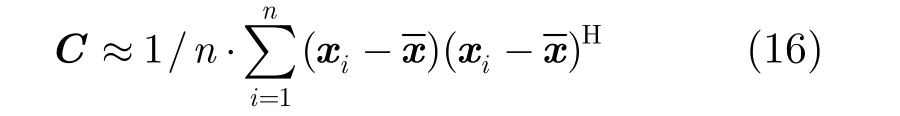
近似计算得到,其中n是训练样本数,x是所有训练样本的平均。

将矩阵A作用在所有训练样本以及待考查模式上,那么计算NR时所选训练样本变为 Axi=Ax0+ζi,i =1,2,…,K ,待考查模式变为 Axk= Ax0+ ζk,k >K,其中 ζi=Aεi为变换后的模式噪声。由于

所以经矩阵A变换后模式中的色噪声变为高斯白噪声。经过与前文一样的计算过程,可得到相同的分析结果,即野值门限与虚警概率的对应关系式(15)。这样利用变换矩阵A就可解决色噪声情形下野值检测虚警率的控制问题。
需要说明的是,在训练样本数较少时,协方差矩阵C难以由训练样本准确估计。此时,可通过先验信息推算C的大小。一个可行的策略是根据原始数据中噪声的分布,以及由数据提取训练/测试样本时所采取的方法计算出样本噪声的协方差矩阵。本文4.2节进行实测数据测试时会给出这方面的例子。下文均假设C是先验已知的。
3.3 野值检测方法
(1)对协方差矩阵C进行特征值分解,利用式(17)计算转换矩阵A,将其作用在训练样本及待考查模式上,使得样本中的噪声被白化。
(2)根据虚警率 Pf的大小,利用式(15)计算野值检测门限h。
(3)对于待考查模式 ηi,在 Xtr中随机选择K个训练样本根据式(4)计算模式 ηi的NR值 ri。
4 实验与分析
4.1 计算机仿真
考虑到本文在处理色噪声模式时可将其白化,所以在仿真实验中只考查白噪声的情况。设正常模式由 x = x0+ε产生,其中 x0是幅度为1,初相为π,2.5倍周期的正弦波, ε ~N( 0, σ2I ),σ2设为 0.04,所以模式的“信噪比”约为11 dB。野值由 x= y0+ε产生,其中 y0是幅度/初相变化的正弦波或者多项式曲线。
首先验证虚警概率与野值门限的关系式(14)的正确性。设模式维度N为50或200,训练样本的个数 n= 60,计算 NR 值时选择的训练样本数K= 16,计算重复次数 B= 10。另产生1000个正常模式和500个野值模式作为测试样本,蒙特卡洛仿真500次,得到的结果如图1所示。可以看出,随着野值检测门限的增加,虚警概率逐渐变小。本文理论推算的 Pf-h关系式(式(14))与实验结果吻合得很好,尤其是当模式维数较高时二者几乎一致,说明本文野值门限理论推导结果的正确性。
其次考查参数设置对本文方法虚警抑制效果的影响。固定虚警概率 Pf= 0.05,分别改变所选训练样本数K和重复计算次数B,其他设置与上一实验相同,得到的虚警概率测试结果如图2所示。可以看出,计算NR值时选择的重复次数B对虚警率的影响比较小,而K的值对虚警率抑制有较大影响,K值太小或太大会分别出现“过抑制”和“欠抑制”的现象。下面的实验要将本文方法和LPE方法进行性能比较,采用统一的参数设置,为兼顾两种方法,下文不做特殊说明时均设 B= 10, K= 16。
带虚警抑制的已有方法中,虽然在一定的实验条件下aK-LPE方法已被证明具有比K-LPE更优的性能[13,14],但是二者在训练样本数较少情况下表现如何尚需实验检验。下面的实验主要考虑将本文方法与这两种方法进行性能对比。

图1 虚警概率随野值门限的变化曲线

图2 不同参数设置条件下本文方法得到的虚警概率
现在考查当训练样本数较少时本文方法对虚警率的抑制效果。设需要的虚警率为 Pf= 0.05,其他设置与第1个实验一致,改变训练样本数n,得到的实际虚警概率如图3所示,其中“NR”是指基于NR的野值检测方法,图3(b)中虚线第1个点的值为0.783,为便于各方法的对比,图中没有显示该点的值。由于文献[10]针对的是无监督情形下的野值检测问题,这里用训练样本代替该文献方法中的初始正常模式集合。该方法的野值检测门限需要依据经验或实验结果人为设置,经过反复测试,为满足虚警率为0.05的要求,将其检测门限设为1.08。注意当训练样本较少时,LPE方法及本文方法可能无法取到所需数目的训练样本,此时可将K值选为能够利用的训练样本数。
由图3可以看出,本文方法在少量训练样本数情况下能够较好地抑制虚警率,使之接近设定值。在即使只有4个训练样本时,本文方法仍能将虚警率抑制在2倍设定值以下,而此时LPE方法的虚警率则超过了设定值5倍以上。而对于文献[10]中的方法,即使野值门限设置得当,也有可能产生很高的虚警。此外图3也表明,模式维数N越大,本文方法对虚警率的抑制效果越好。这是由于N越大,3.2节推导野值门限过程中的近似越准确,此时依据式(15)设置检测门限能更好地控制虚警率。
需要说明的是,文献[10]提出的方法是无监督的,且没有在野值检测门限与虚警率之间建立直接的联系,其检测门限需要主观的人为设置,无法根据虚警率大小预先选择合适的门限值,所以无法实现真正意义上的虚警控制。鉴于它与本文方法及LPE方法本质上不属同类,下面的实验不再考虑该方法。
除虚警率外,野值检测概率也是重要的性能指标,下面测试本文方法的接收机工作特性(Receiver Operating Characteristic, ROC)曲线。设训练样本数 n= 20,模式维数N为50或200,设置不同的虚警率,蒙特卡洛仿真200次,测试得到的ROC曲线如图4所示,其中“NR”即指本文方法,这一表示同样适用于后续实验,横轴所示的虚警率指的是实际虚警率。可以看出,在较高虚警率条件下本文方法与aK-LPE方法性能相当,说明此时本文方法也可达到 UMP检验的效果。但是本文所提野值检测方法能够满足更低虚警率的要求,所以具有更优的综合检测性能。
4.2 实测数据测试

图3 不同训练样本数目条件下的虚警概率测试结果
实测数据测试的场景是:由于分选错误或者干扰的存在,某雷达辐射源的一组信号中混入了其他源的信号,一般需要根据信号的特征参量对混入信号进行判别。提取这些信号的特征参量后,经过人工判断,选出其中一部分特征参量,认为它们来自感兴趣的辐射源,将其作为训练样本。由于人工挑选比较耗时,得到的训练样本数量并不多。现在面临的问题是,根据已有的训练样本,在一定虚警概率的要求下,需对其他特征参量进行野值检测,从而避免混入信号的影响。

图4 野值检测概率随虚警概率变化的ROC曲线
本文的测试对象是民航飞机的二次雷达(Secondary Surveillance Radar, SSR)信号,它是一种单载频形式的窄脉冲信号。提取信号的瞬时相位[19]作为考查的特征参量,经过特征平滑,易得特征提取结果为

选择一组SSR信号,它们来自同一辐射源 E0,在这组数据中混入其他两个辐射源 E1和 E2的信号。本实验共接收到了69个辐射源的数据,对辐射源按1到69编号,并设 E0= 1,E1= 2,E2= 4。按照式(19)进行特征提取,随机选择 E0的一部分特征参量作为训练样本,由此对其他样本进行野值检测。考查不同训练样本数时,虚警率设为考查ROC曲线时,训练样本数设为 n= 20。测试样本由1000个正常模式(即属于 E0的模式)和来自不同源共600个野值模式组成。野值检测时需要考虑特征提取过程中引入的协方差矩阵C,按照 3.3节给出的方法流程进行处理,得到的测试结果如图5所示。图中数据是100次测试的平均结果。可以看出,对于实测数据,在较少训练样本条件下本文方法仍然能够较好地抑制虚警率,效果优于同类方法。此外其 ROC曲线也较理想,表明其优越的野值检测性能。
保持参数设置不变,表1给出了混入其他辐射源信号情况下,不同方法野值检测结果 ROC曲线的线下面积(Area Under the Curve, AUC)大小,其中“维数”是指混入信号的最小样点数。可以看出,对于所有测试集,本文提出的方法都具有最优的AUC性能。
5 结束语
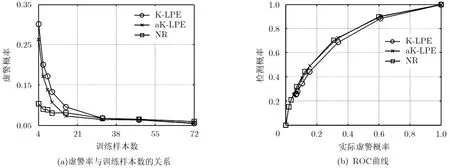
图5 实测数据测试得到的野值检测结果
本文考虑了带监督情形下野值检测的虚警抑制问题,提出了一种基于归一化残差的野值检测方法。该方法利用训练样本重新定义了模式的归一化残差,据此,本文推导得到了野值检测门限与虚警概率之间的关系表达式,为野值门限的设置和野值判别提供了理论依据。仿真实验和实测数据测试验证了本文理论推导的正确性,以及少量训练样本情况下所提方法在野值检测和虚警抑制方面的优越性能。

表1 对不同数据集进行野值检测得到的AUC大小
需要指出的是,本文方法可以适应高斯白噪声以及能推导出协方差矩阵的色噪声情形,对于更复杂的噪声模式,则需要对野值检测门限进行重新推算以满足控制虚警概率的要求。这一点可作为下一步的研究方向。
[1] Hawkins D. Identification of Outliers[M]. London: Chapman and Hall, 1980: Chapter 1-2.
[2] Liu J, Wan J, Zheng H, et al.. A method of specific emitter verification based on CSDA and SVDD[C]. Proceedings of the IEEE 2nd International Conference on Computer Science and Network Technology, Changchun, China, 2012: 562-565.
[3] Miller D J and Browning J. A mixture model and EM-based algorithm for class discovery, robust classification, and outlier rejection in mixed labeled/unlabeled data sets[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(11): 1468-1483.
[4] Westerweel J and Scarano F. Universal outlier detection for PIV data[J]. Experiments in Fluids, 2005, 39(6): 1096-1100.
[5] Duncan J, Dabiri D, Hove J, et al.. Universal outlier detection for Particle Image Velocimetry (PIV) and Particle Tracking Velocimetry (PTV) data[J]. Measurement Science and Technology, 2010, 21(5): 57002-57006.
[6] Wu S and Wang S R. Information-theoretic outlier detection for large-scale categorical data[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(3): 589-602.
[7] Li Z G, Baseman R J, Zhu Y D, et al.. A unified framework for outlier detection in trace data analysis[J]. IEEE Transactions on Semiconductor Manufacturing, 2014, 27(1): 95-103.
[8] Albanese A, Pal S K, and Petrosino A. Rough sets, kernel set,and spatiotemporal outlier detection[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(1): 194-207.
[9] Ghosh A K and Chaudhuri P. On maximum depth and related classifiers[J]. Scandinavian Journal of Statistics, 2005,32(2): 327-350.
[10] Ru X H, Liu Z, and Jiang W L. Normalized residual-based outlier detection[C]. Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 2014: 190-193.
[11] Nattorn B, Arthorn L, and Krung S. Outlier detection score based on ordered distance difference[C]. Proceedings of the IEEE International Computer Science and Engineering Conference (ICSEC), Nakhon Pathom, Thailand, 2013: 157-162.
[12] Zhao M and Saligrama V. Anomaly detection with score functions based on nearest neighbor graphs[J]. Advances in Neural Information Processing Systems, 2009, 22(1): 2250-2258.
[13] Qian J and Saligrama V. New statistic in p-value estimation for anomaly detection[C]. Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, Michigan,USA, 2012: 393-396.
[14] Chen Y T, Qian J, and Saligrama V. A new one-class SVM for anomaly detection[C]. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Vancouver, Canada, 2013: 3567-3571.
[15] Breunig M M, Kriegel H-P, Ng R T, et al.. LOF: identifyingdensity-based local outliers[C]. Proceedings of the ACM SIGMOD International Conference on Management of Data,New York, USA, 2000: 93-104.
[16] Schölkopf B, Platt J C, Shawe-Taylor J C, et al.. Estimating the support of a high-dimensional distribution[J]. Neural Computation, 2001, 13(7): 1443-1471.
[17] Furlani M, Tuia D, Munoz-Mari J, et al.. Discovering single classes in remote sensing images with active learning[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany,2012: 7341-7344.
[18] Jumutc V and Suykens J. Multi-class supervised novelty detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(12): 2510-2523.
[19] 叶浩欢, 柳征, 姜文利. 考虑多普勒效应的脉冲无意调制特征比较[J]. 电子与信息学报, 2012, 34(11): 2654-2659. Ye H H, Liu Z, and Jiang W L. A comparison of unintentional modulation on pulse features with the consideration of Doppler effect[J]. Journal of Electronics & Information Technology, 2012, 34(11): 2654-2659.
汝小虎: 男,1988年生,博士生,研究方向为雷达辐射源识别.
柳 征: 男,1978年生,博士,副研究员,研究方向为综合电子战信息战技术、航天电子侦察信号处理.
姜文利: 男,1967年生,博士,教授,博士生导师,研究方向为综合电子战信息战技术、航天电子侦察信号处理.
黄知涛: 男,1976年生,博士,教授,博士生导师,研究方向为综合电子战信息战技术、卫星通信侦察与对抗.
Normalized Residual-based Outlier Detection with False-alarm Probability Controlling
Ru Xiao-hu Liu Zheng Jiang Wen-li Huang Zhi-tao
(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Outlier detection, also called anomaly detection, is an important issue in pattern recognition and knowledge discovery. Previous outlier detection methods can not effectively control the false-alarm probability. To solve the problem, a supervised method based on Normalized Residual (NR) is proposed. Using the training patterns, it first calculates the NR value of the query pattern, which is compared with a predefined detection threshold to determine whether the pattern is an outlier. In this paper, the relationship between the threshold and false-alarm probability is theoretically derived, based on which an appropriate threshold can be chosen. In this way,the desired false-alarm probability can be obtained even when few training patterns are available. Simulations and measured data experiments validate the superior performance of the proposed method on outlier detection and false-alarm probability controlling.
Pattern recognition; Supervised; Outlier detection; False-alarm probability; Normalized Residual (NR)
TP391.4; O235
A
1009-5896(2015)12-2898-08
10.11999/JEIT150469
2015-04-22;改回日期:2015-09-01;网络出版:2015-11-01
*通信作者:汝小虎 ruxiaohu88@163.com

