安徽省全要素生产率的测算与经济解释——基于时变产出份额改进的索洛残差法

程建华，于戒严

（安徽大学 经济学院，安徽 合肥 230601）

·华东经济

安徽省全要素生产率的测算与经济解释
——基于时变产出份额改进的索洛残差法

程建华，于戒严

（安徽大学 经济学院，安徽 合肥 230601）

文章运用状态空间模型推导出C-D生产函数的时变要素产出份额，并以此改进索洛残差法计算安徽省1992-2012年的TFP增长率，实证分析结果发现，安徽省TFP增长率变动趋势与全省宏观经济运行高度吻合，其变化滞后于长三角地区大约2年时间，但近年来变化时差逐步趋同。计量结果显示：安徽省1992-2012年平均TFP增长率为1.13%，相对较高；TFP增长率是GDP增长率的Granger原因，反之则不成立；安徽省经济增长属于资本投入型，技术进步对经济增长的平均贡献率仅为7%，缺乏效率。最后得出促成技术进步的内生增长动力、提升人力资本的潜在增长动力、保证资本等实体要素的基础支撑力是未来安徽省经济持续稳定发展的根本保证。

时变弹性；状态空间模型；索洛残差；全要素生产率（TFP）

［DOI］10.3969/j.issn.1007-5097.2015.01.005

一、引　言

全要素生产率（Total Factor Productivity，简记为TFP）是指生产过程中全部投入要素（资本、劳动等）转变为实际产出的效率，是总产出与综合投入要素之比，其研究对象是在一个经济系统中，所有投入要素加权综合后形成综合投入的产出效率，反映的是一个经济系统的宏观综合经济效益。具体而言，全要素生产率是指扣除了资本、劳动等要素投入的贡献以外，其他所有能够实现经济增长的因素贡献的总和。这个总和的来源包括技术进步、资源配置效率的提高（主要体现为体制的更加完善）以及其他随机因素等。TFP也是分析经济增长源泉的重要工具，通过分析各种因素对经济增长的贡献，可以识别经济增长的类型究竟是投入型还是效率型，从而确定经济增长的可持续性。与衡量某一时期静态经济效率水平的全要素生产率不同，全要素生产率增长率是指总产出增长率减去要素加权投入增长率的余值，是衡量经济增长效率变化的动态指标，即反映动态的经济增长效率水平［1］。这一计算方法最早由索洛（Solow，1957）提出，因此也称为索洛残差。本文TFP专指技术进步，与郭庆旺、贾俊雪（2005）一文中的TFP有所区别，该文中的TFP还包含技术进步和能力实现改善［2］；赵志耘、杨朝峰（2011）定义TFP为技术进步（包含技术引进和自主创新）和体制完善［3］，Fare等（1994）把TFP增长率分解为技术进步率和技术效率两大部分［4］。然而技术进步是促进高技术产业全要素生产率增长的主要源泉（宋慧勇、章仁俊，2014）［5］，中国旅行社业的经营效率增长主要来自于技术进步（赵海涛、高力，2013）［6］，中观层面各行业的全要素生产率大体取决于技术进步，因此本文以中观经济为基础、抓住关键因素，将安徽省宏观经济运行的全要素生产率界定为技术进步。

TFP有多种测算方法，主要分为参数方法和非参数方法。参数方法包括代数指数法、索洛残差法、隐性变量法、潜在产出法和前沿生产函数法等；非参数方法包含Malmquist指数方法和HMB指数方法等。郭庆旺、贾俊雪（2005）在分析比较了全要素生产率四种参数估算方法的基础上，估算出我国1979-2004年间的全要素生产率增长率，并分析了我国全要素生产率增长和经济增长源泉，结果表明我国经济增长主要依赖于要素投入，TFP的贡献较低。李宾、曾志雄（2009）使用并延展Holz （2006）的资本存量序列，通过要素收入份额可变的增长核算法，重新审视我国1978-2007年的TFP增长率［7］。周晓艳、高春亮、李钧鹏（2009）采用随机前沿模型对1990-2006年长三角地区的生产效率进行估算并分解其全要素生产率增长率［8］。

本文通过时变弹性的Cobb-Douglas生产函数（以下简称C-D生产函数）构建可变要素产出份额的索洛模型，利用安徽省1991-2012年经济数据计算全省全要素生产率增长率，以此重新审视在我国当前宏观经济“稳增长、防通胀、调结构、促转型”的大背景下地方经济未来的发展方向、新的经济增长点或增长路径。

二、全要素生产率测算模型

本文将对传统索洛模型进行改进，以状态空间模型所估计出来的时变资本和劳动的产出份额代替传统的恒定弹性系数，以此获得全要素生产率更为精微的测算值。

（一）索洛残差模型

索洛残差法的基本思路是估算出总量生产函数后，以产出增长率扣除各投入要素增长率贡献之后的余额作为全要素生产率增长率。在规模报酬不变和希克斯（Hicks）中性技术假设下，全要素生产率增长率就等于技术进步率。因此该模型实质上认为产出增长是生产要素（资本、劳动等）投入和技术进步联合作用的结果。

总量生产函数通常采用C-D生产函数，其随机形式方程如下：

其中，Yt为真实产出；At为随时间变化的技术进步；Lt为劳动投入；Kt为资本存量；α、β分别为平均资本产出份额和平均劳动产出份额，也即产出的资本弹性和产出的劳动弹性；ut为随机扰动项。两边同时取自然对数有：

ln Yt=ln At+αln Kt+βln Lt+ut（2）

在规模报酬不变和希克斯（Hicks）中性技术假设下，将（2）式确定性部分（即不考虑随机扰动项）两边对时间微分得：

移项后可表示为：

a=y-αk-βl（4）

其中，a=∂A/A表示技术进步增长率也即全要素生产率增长率，y=∂Y/Y表示真实产出增长率，k=∂K/K表示资本存量增长率，l=∂L/L表示劳动力增长率。

除上述计算表达式外，还可以通过如下方法计算资本、劳动和全要素生产率对经济增长的贡献率：

其中，CK、CL、CA分别表示资本、劳动和全要素生产率对经济增长的贡献率。

在规模报酬不变即α+β=1的假设下，有回归方程：

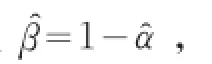
（二）时变弹性的C-D生产函数

如果事先假定各年的资本和劳动产出弹性相同，从而也就否定了要素结构变化对产出的影响［9］。有鉴于此，本文运用状态空间模型估算时变弹性。将弹性系数视为两个不可观测的潜变量，从而借助状态空间模型（State Space Model）利用卡尔曼滤波算法给出两个时变弹性系数αt、βt的估计值。

设如下状态空间模型：

其中，（7）式为量测方程（Measure Equation）；（8）式、（9）式为状态方程（State Equation）；αt、βt为状态变量，均服从带有常数项的AR（1）过程。

在得到时变的平均资本产出份额αt和平均劳动产出份额βt的估计值后，将其带入（4）式即可求出全要素生产率的增长率。进而由（5）式可求出资本、劳动和全要素生产率对经济增长的贡献率。采用C-D生产函数的时变弹性来测算全要素生产率具有一定优越性：一方面通过求解出弹性系数可以比较直观清晰地看到是否满足规模报酬不变的假设；另一方面在满足规模报酬不变的假设下，用时变弹性代入索洛残差模型，能够捕捉到TFP更细微的变化，使结果更精确也更符合实际情况。

三、安徽省全要素生产率的测算

（一）指标选取与数据处理

鉴于数据的可得性与准确性，本文选取安徽省1991-2012年的年度数据进行实证分析。本文需要真实产出、资本存量和劳动投入数据。以工业品出厂价格指数代替GDP平减指数并转化为1991年为基期的定基指数，然后以此定基指数缩减名义GDP得出代替真实产出的实际GDP数据。以全省经济活动人口数表示劳动力投入量。下面重点介绍资本存量的估算。

本文采用Goldsmith于1951年开创的永续盘存法［10］测算资本存量，其表达式为：

其中，Kt为t年的实际资本存量，Kt-1为t-1年的实际资本存量；It为t年的名义投资流量；Pt为固定资产投资价格指数；δt为t年的固定资产的折旧率。

本文以安徽全省固定资产投资额作为资本流量It，并以1991年为基期的固定资产投资价格指数Pt对It进行价格缩减，折旧率采用我国一般的综合折旧率δ=5%，基期实际资本存量K0按照以下国际常用方法计算K0=I0/（δ+g），其中g是样本期实际资本流量的年平均增长率，经计算g=19.04%，则基期即1991年实际资本存量K0=173.30/（5%+19.04%）=571.17。在确定了资本存量的初值以及实际投资后，按（10）式即可计算各年份的实际资本存量。具体数据参见表1中2-4列。

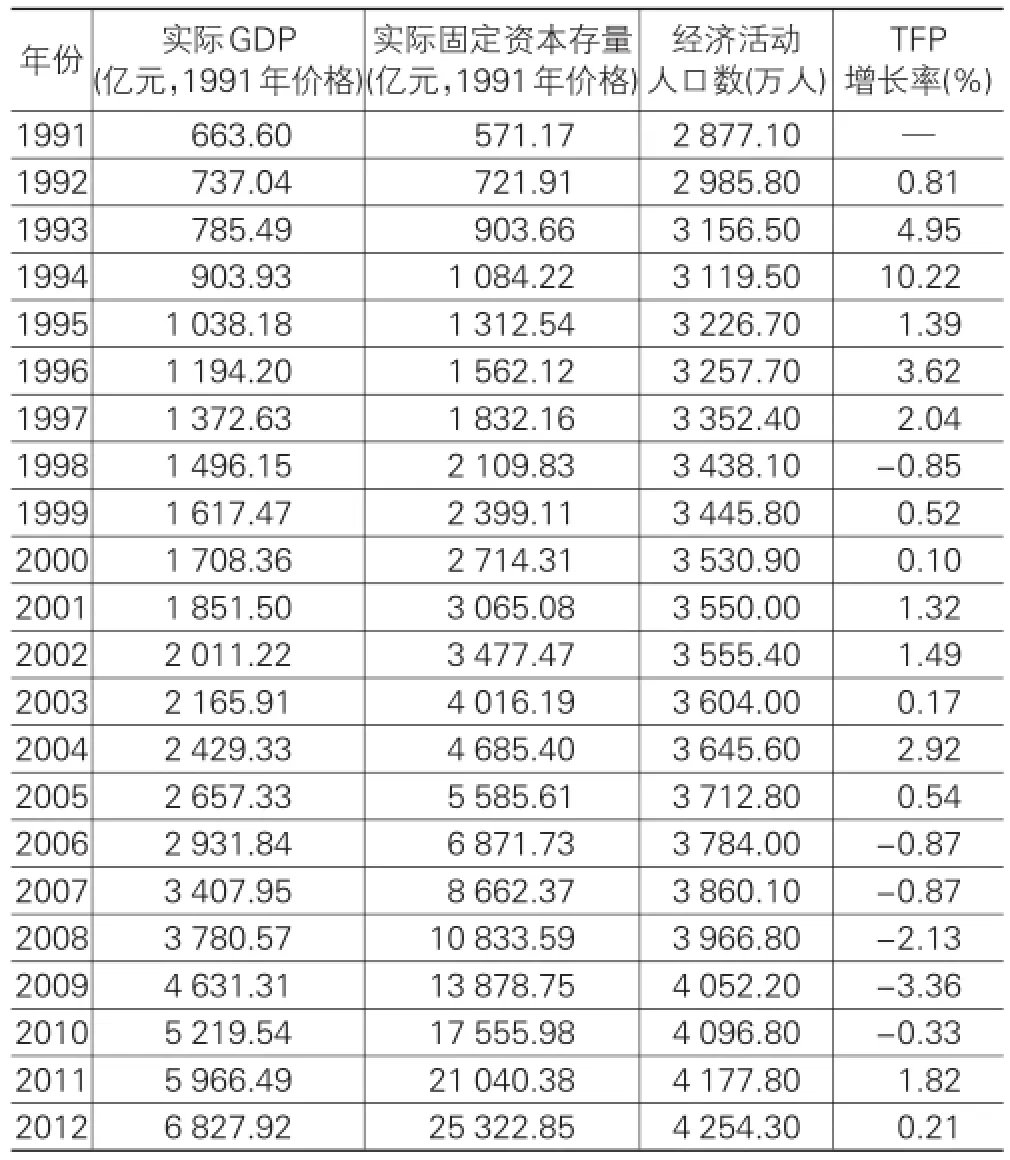
表1　安徽省经济生产数据和TFP增长率

根据折价和折算后的安徽省产出过程相关经济数据（表1中实际GDP、固定资本存量和经济活动人口数），构建测算安徽省TFP增长率的具体模型并分析其经济意义。

（二）平稳性检验

由于lnY、lnK、lnL都呈线性趋势，宜选择带有截距项的ADF检验方程，以SIC准则确定滞后阶数，检验结果如表2。由于三者ADF的绝对值都较小，而相应的伴随概率都较大，所以不能拒绝原假设，因此可认为这三者都不满足平稳性。取其一阶差分再进行单位根检验，获得ADF值相应的伴随概率都小于5%，从而在5%的显著性水平下可认为lnY、lnK、lnL三者的一阶差分满足平稳性，即它们都是一阶单整序列I（1）。

表2　变量单位根检验结果

（三）协整检验

为了避免伪回归现象发生，有必要对lnY、lnK、lnL三者之间是否具有协整关系进行检验。由平稳性检验结果可知三者是同阶单整序列，故可以进行协整检验。协整检验一般包括基于回归系数的协整检验和基于回归残差的协整检验（EG法），本文采用基于回归系数的JJ检验，检验结果见表3所列，迹统计量和最大特征根统计量相一致，拒绝lnY、lnK、lnL三者无协整向量的原假设，而接受至多1个协整向量的原假设，所以得出三者之间存在一个协整向量，具有长期稳定协整关系，可以对三者进行回归分析。

表3　JJ协整检验结果

（四）恒定弹性C-D生产函数的构建

首先检验安徽省生产过程是否满足规模报酬不变的假设。建立ln（Yt）=ln（A）+αln（Kt）+βln（Lt）+ut并修正序列相关性，然后对系数进行Wald检验，原假设H0:α+β=1，即规模报酬不变。由于只有一个约束条件，所以经计算χ2统计量和F统计量相等，均为1.59，相应的伴随概率p=0.224 2＞5%，所以不能拒绝原假设，认为规模报酬不变，满足索洛模型的前提条件。

在规模报酬不变的前提下，可建立下列模型：

虽然变量都通过了显著性检验，而且模型整体的拟合优度也相当满意，但由于D.W.值偏小，残差可能存在一阶正序列相关。进一步地，从残差图（图1）折线穿过零轴的次数很少说明残差不符合白噪声过程，残差存在正的序列相关。

图1　残差序列

表4　序列相关性的LM检验

运用广义差分法对方程（11）进行修正，修正后的模型如下：

（五）时变要素产出份额的C-D生产函数

本文构建相应的状态空间模型，并利用极大似然法估计模型参数，其结果如下：

由极大似然法估计的结果可知αt、βt的滞后一期的系数估计值在5%的显著性水平下都是显著的。以滤波估计结果作为状态变量αt、βt的估计值如图3所示。从集中趋势看，αt、βt的均值分别为0.55、0.42，与上述固定弹性基本相同；从标准差来看，两者的离散程度都非常小，即只存在轻微波动，αt、βt较为稳定（见表5）。从时序图来看，两者具有同趋势波动规律，说明安徽省生产过程中资本和劳动具有很好的协同作用。另外，αt、βt之和在各年份也基本接近于1，与上文Wald检验相一致，直观与实证结果均表明近20年来安徽省一直处于规模报酬不变的经济增长过程。将时变要素份额带入（4）式即可求得TFP增长率，具体结果即为表1中最后一列数据。

图3　产出的资本弹性α和产出的劳动弹性β序列

表5　产出的资本弹性α和产出的劳动弹性β描述统计量

四、基于TFP增长变化的安徽省经济增长分析

（一）TFP增长变化与对比分析

本文基于时变参数的产出资本弹性和劳动弹性测算出全要素生产率增长率如图4，容易看出安徽省TFP增长率波动趋势与全省GDP增长率变化趋势高度吻合。1992年以后随着社会主义市场经济体制的逐步建立和改革开放程度的进一步扩大，TFP增长率在1994年达到了峰值10.22%，其主要原因是此阶段大量引进国外先进技术。但为应对1993-1995年高通货膨胀①所实施的紧缩性宏观调控政策和国有企业改革的艰难进行导致TFP迅速下滑，特别是1997年东南亚金融风暴的袭击不但使安徽省TFP持续走低，且使1998年TFP出现了负增长。2000年以后随着国家宏观经济形势逐步好转，特别是2001年我国加入WTO后，安徽经济也开始小幅企稳回升，TFP增长率缓慢上升，并于2004年再次达到一个新的峰值。2006年开始由于大量的投资拉动全省经济增长进一步提升，由于要素投入的粗放式增长缺乏效率致使TFP增长率再次出现大幅下滑。2008年由美国次贷危机引发的全球金融危机对安徽经济的负面影响远远大于1997年亚洲金融危机。宏观经济的低迷大大抑制了企业研发创新能力，依赖投资拉动的短期“保增长”目标实现与2009年的-3.36%TFP增长率形成鲜明对比。2010-2012年安徽省TFP增长率的小幅波动印证了安徽乃至国家经济实施“稳增长、调结构、促转型”政策的必要性和迫切性。

图4　安徽省全要素生产率增长率与全省GDP增长率时序

与之前相关文献测算的TFP增长率对比分析发现，周晓艳等（2009）测算的1991-2006年长三角地区（沪、浙、苏）的全要素生产率增长率的变化三省（市）基本一致，且本文测算的安徽省TFP增长率的变动与之也基本相似。进一步分析发现1992-2003年间长三角地区TFP变化在时间上领先安徽省2年左右，但平均值低于安徽省。长三角地区TFP增长率在1992年达到峰值（5%左右）、1996年到达谷底（-2%左右），而安徽省在1994年达到峰值（10.22%）、1998年达到谷底（-0.85%）。值得注意的是，安徽省和长三角地区几乎都在2004年同时达到峰值且增长率均为2%左右，同时考虑到近年来皖江城市带承接产业转移示范区的建立与发展，安徽省近10年来与长三角地区TFP增长变化趋同，由此表明安徽省正逐步融入长三角地区经济圈。

本文测算的安徽省TFP增长率平均为1.13%，周晓艳等（2009）测算的1991-2006年上海、江苏、浙江TFP增长率平均分别为0.72%、0.4%、0.4%。忽略样本期间的差异②，长三角地区平均TFP增长率低于安徽，主要表现在长三角于1994-2000年TFP增长率一直处于负值，而安徽同期仅在1998年处于负值。长三角地区TFP增长率较低有其内在原因，长三角地区对外开放程度大，通常采用引进技术设备和购买专利技术来提高技术进步，这些机器设备中一般都嵌入了发达国家的技术创新［11］，因此是一种与资本融合在一起的技术进步［12］。长三角地区产出的资本弹性为0.747，而安徽产出的资本弹性仅为0.55，正是由于与资本融合在一起的技术进步才导致长三角地区如此之高的产出的资本弹性。因此其TFP增长率比较低，只说明不包括资本投入的技术进步比较低。从而不能从表象上得出安徽经济增长的效率好于长三角地区的结论。另外，郭庆旺、贾俊雪（2005）测算的我国1979-2004年技术进步率（相当于本文的TFP增长率）为0.954%，安徽省TFP增长率略高于全国平均水平。

然而TFP与GDP究竟何为因何为果？需要通过Granger因果关系检验具体说明。通过表6可以看出，TFP是GDP的Granger原因，反之不成立。此表明技术进步对经济增长具有促进作用，但经济增长并没有内生性的促进技术进步。安徽省生产技术在一定程度上是个外生变量，更多的是靠外部引进技术，这一点同全国的情况基本相同。我国改革开放30年来，对外开放程度不断加大，经济增长举世瞩目，然而与此同时，体制改革、技术创新却大大落后。时至今日，人口红利、开放红利逐渐萎缩，迫使中央政府和学术界开始寻求新的经济增长点，力图通过深层次的改革、体制完善和创新来激发市场活力。一方面政府应积极引导企业的创新意识，营造良好的知识产权开发与保护环境。如果创新者拥有创新成果的产权从而享有其成果的收益，创新就获得了足够的激励，因此产权决定创新能力［13］。另一方面企业自身更要从长远发展考虑，增加研发资金投入，加大研发力度，同时加强校企合作，充分利用高校的科研能力优势，快速提高技术进步，从而能够大大提高企业竞争优势，实现经济发展方式的转变。

表6　TFP和GDP的Grange因果关系检验

（二）因素贡献率分析

从资本、劳动和TFP对安徽省经济增长的贡献率分析（见表7、图5），资本贡献率几乎在各年份（1994年除外）均远远高于劳动和TFP的贡献率，1992-2012年间平均资本贡献率高达86.83%，而平均劳动贡献率和平均TFP贡献率基本相当。可以认为安徽省经济是资本投入型的经济增长方式，技术进步对经济增长的贡献率太低，平均仅近7%，经济增长缺乏效率。郭庆旺、贾俊雪（2005）测算的我国1979-2004年技术进步率对经济增长的贡献为10.13%。从前文可知安徽TFP增长率平均值略高于全国，但技术进步对经济增长的贡献率却低于全国水平，忽略样本期间的差异，主要由于1992-2012年间安徽GDP增长率全部高于全国GDP增长率，这样由（5）式计算出的安徽技术进步对经济增长的贡献会偏低。从三者标准差来看，TFP贡献率变异最大，安徽省技术进步主要靠外部引进，受外部冲击的反应较敏感，因此安徽企业应开发自己的核心技术，免受外部冲击的影响，从而对经济增长产生持续的拉动作用。劳动贡献率的平均值和标准差均最小，安徽省虽是人口和剩余劳动力大省，但劳动力对经济增长的贡献率多年来却一直很低。究其原因，一方面，多年来安徽大量剩余劳动力外流，劳动大军涌入长三角、珠三角等沿海地区，从而使得本省人力资本反而相对匮乏；另一方面，在安徽劳动力大军涌向经济发达地区的同时，本省劳动力综合素质得不到及时提高，特别是高技能、技术型和创新型人才大量流失致使安徽经济增长的劳动和技术贡献率降低。

表7　1992-2012年间经济增长的各因素平均贡献率

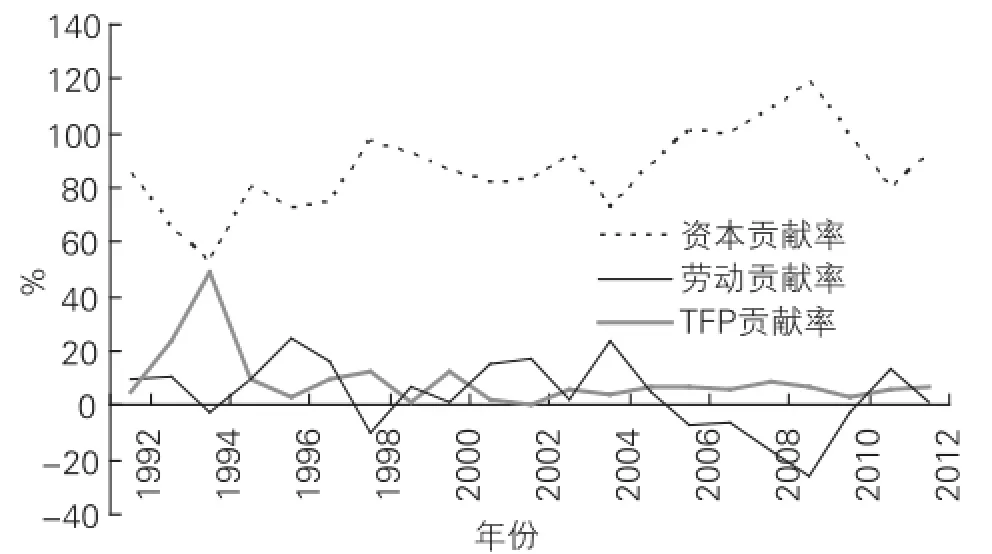
图5　1992-2012年经济增长的各因素贡献率

五、结束语

本文运用状态空间模型构建时变弹性的C-D生产函数，从而得到可变资本和劳动的产出份额，并以此改进传统的索洛模型，测算出安徽省1992-2012年的TFP增长率。规模报酬不变的C-D生产函数很好地拟合了安徽省生产数据，且时变资本和劳动的产出份额之和非常接近于1，满足索洛模型规模报酬不变的前提假设，在此基础上成功地估算TFP增长率。

通过与全国和长三角对比分析表明本文测算的安徽省TFP增长率较为可靠，纵向上符合安徽经济运行过程，与其高度吻合；横向对比看，安徽省1992-2012年平均TFP增长率为1.13%，相对较高，前10年滞后于长三角地区TFP增长率变化2年，后10年趋同，表明安徽省也在逐步融入长三角的发展。1992-2012年间平均资本贡献率高达86.83%，TFP贡献率仅近7%，劳动贡献率仅6.24%。因此安徽省是资本投入型经济增长方式，而非效率型。

安徽省TFP增长率是GDP增长率的Granger原因，反之不成立。表明技术的进步确实为经济的发展起到重要推动作用，但经济的发展并没有内生地提高技术进步，技术进步很大程度依靠引进，教育、养老、财税、金融等各方面体制需要进一步完善，自主创新能力有待加强。

基于以上安徽经济增长的分析结果，本文得出三点有益启示，也可视为政策建议。

第一，促成技术进步的内生增长动力。政府应继续加大公共教育和科技等投入，同时加快转变政府职能，深层次完善体制，不断提高资源配置和运用的效率，提升技术进步率；企业应提高创新意识，不断改善生产管理和公司治理水平，提高生产经营效率。促使技术进步成为推动经济发展的内生动力。

第二，提升人力资本的潜在增长动力。在产业结构调整方面，与长三角分工合作、优势互补、一体化发展，从而调整就业结构。依托产业结构调整，吸纳大批高素质人才，在各产业领域优化技术工人、高级管理人员、科研人员的结构比例，从而激发人力资本推进经济增长的强大潜在动力。

第三，保证资本等实体要素的基础支撑力。未来一段时期，实体资源要素投入依然是安徽经济稳增长的主导途径，当前快速发展的城镇化，仍然要发挥资本、土地等要素推动经济发展的基础性作用，但与此同时充分考虑资源配置的效率。现阶段生态环境问题尤其是空气质量恶化已成为制约经济发展的最大阻力，因此，优化资源要素的合理配置刻不容缓。

总之，围绕产业升级和培育新的经济增长点，积极吸纳资本、技术、管理、人才、品牌等要素，使之形成强劲合力，有效保证安徽经济的可持续均衡稳步发展。

注释：

① 安徽省年度CPI 1994年为26.9%，达到了历史峰值，1995年为14.8%，1996年为9.9%。

②本文测算的安徽省1992-2006年间TFP平均增长率为1.89%，因此同期相比，安徽TFP增长率仍高于长三角地区。

［1］李福柱，杨跃峰.全要素生产率增长率的测算方法应用述评［J］.济南大学学报：社会科学版，2013，23（2）：64-68.

［2］郭庆旺，贾俊雪.中国全要素生产率的估算：1979-2004 ［J］.经济研究，2005（6）：51-60.

［3］赵志耘，杨朝峰.中国全要素生产率的测算与解释：1979-2009年［J］.财经问题研究，2011（9）：3-12.

［4］Fare R，Grosskopf S，Norris M，et al.Productivity Growth，Technical Progress，and Efficiency Change in Industrialized Countries［J］.American Economic Review，1994，84（1）：66-83.

［5］宋慧勇，章仁俊.基于DEA-Malmquist的高技术产业研发效率变动分析［J］.企业经济，2014（6）：100-104.

［6］赵海涛，高力.中国旅行社业经营效率的动态变化——基于 Malmquist指数法的分析［J］.企业经济，2013（2）：114-117.

［7］李宾，曾志雄.中国全要素生产率变动的再测算：1978-2007年［J］.数量经济技术经济研究，2009（3）：3-15.

［8］周晓艳，高春亮，李钧鹏.我国长三角地区经济增长因素的实证分析［J］.数量经济技术经济研究，2009（3）：32-55.

［9］段文斌，尹向飞.中国全要素生产率研究评述［J］.南开经济研究，2009（2）：130-140.

［10］Goldsmith R W.A Perpetual Inventory of National Wealth，Studies in Income and Wealth［R］.New York：NBER，1951.

［11］张小蒂，李晓钟.对我国长三角地区全要素生产率的估算及分析［J］.管理世界，2005（11）：59-66.

［12］Chen Edward K Y.The Total Factor Productivity Debate：Determinants of Economic Growth in East Asia［J］.Asian-Pacific Economic Literature，1997，11（1）：18-38.

［13］易纲，樊纲，李岩.关于中国经济增长与全要素生产率的理论思考［J］.经济研究，2003（8）：13-20.

［责任编辑：余志虎］

Calculation and Economics Explanation on Total Factor Productivity in Anhui Province —Solow Residual Method Based on the Time-varying Output Share Improvement

CHENG Jian-hua，YU Jie-yan
（School of Economics，Anhui University，Hefei 230601，China）

This paper deduces the time-varying factor output share of Cobb-Douglass productive function using the state space model，and improves the Solow residual method to calculate the TFP growth rate ofAnhui province from 1992 to 2012.The empirical analysis indicates that the change trend of TFP growth rate in Anhui is highly consistent with the province's macroeconomic performance，and lags behind the Yangtze River Delta region about two years，but the change time is gradually convergent in recent years.The measurement results show that：the average annual TFP growth rate of Anhui is 1.13%from 1992 to 2012，which is relatively high；TFP growth rate is Granger cause of GDP growth，not vice versa；Anhui economic growth is due to capital investment，whereas the average contribution of technological progress to economic growth is merely 7%，less efficient.Finally，the paper draws the following conclusions：promoting the endogenous growth momentum of technological progress，enhancing the potential growth impetus of human capital and ensuring the supporting force of capital and other physical elements are the fundamental guarantee for the sustainable and stable economic development of Anhui province in the future.

time-varying elasticity；state space model；Solow residual；total factor productivity（TFP）

于戒严（1985-），男，安徽宿州人，硕士研究生，研究方向：经济周期与经济预测。

F061.5；F222.33

A

1007-5097（2015）01-0025-07

2014-06-14

国家社会科学基金重大项目（11&ZD011）；国家社会科学基金一般项目（12BJL024）

程建华（1964-），男，安徽泾县人，副教授，工学博士，研究方向：经济周期与经济预测；