行波磁场对板坯连铸结晶器内钢水流态的影响

屠挺生,邓 康,张振强,任忠鸣

(上海大学材料科学与工程学院上海市现代冶金与材料制备重点实验室,上海 200072)

行波磁场对板坯连铸结晶器内钢水流态的影响

屠挺生,邓 康,张振强,任忠鸣

(上海大学材料科学与工程学院上海市现代冶金与材料制备重点实验室,上海 200072)

针对板坯连铸过程中,结晶器内钢水在行波磁场(电磁搅拌)作用下的流动行为,采用水银作为模拟工质进行模型实验,并结合基于流场雷诺应力模型的数值模拟,分析钢水的流动规律及其对连铸工艺的影响.研究结果显示,施加行波磁场(电磁搅拌)时,结晶器内钢水注流的对称性发生了改变,进流被电磁力推向一侧,在结晶器内形成全区域的水平环流,破坏了通常钢水注流所呈现的规律性上下环流;在结晶器上部近液面区域内,水口两侧的环流分别被压缩到靠近水口或窄面的位置,从而使结晶器内流场趋于紊乱的三维流态;同时,液面波动幅度增大,在钢水注流与电磁力反向的一侧,液面波动更加剧烈.

板坯连铸;行波磁场;电磁搅拌;钢水流动;雷诺应力模型

板坯连铸是生产车辆、船舶、家电用钢材的重要工序.随着市场需求的增加和生产工艺向高质、高速和高效方向发展,运用电磁场来控制连铸结晶器内钢水的流动,以实现高连铸速度下的工艺顺行并提高板坯质量,已成为必不可少的重要手段.电磁搅拌(electromagnetic stirring,EMS)是利用钢水的导电性和行波磁场(AC型)定向移动的特性来驱动结晶器内钢水沿特定方向运动,以达到去除夹杂物、降低成分偏析、改善凝固条件和优化连铸工艺的目的[1].

在连铸过程中,将交变电流输入行波磁场搅拌器时,其在结晶器内产生的磁感应强度为

式中,t为时间,x为水平位置,τ为极距.此时,钢水中感生的电流密度为

式中,J0为钢水表面的感应电流密度,y为钢水表面的内法向距离,δ为交变电磁场在钢水中的渗透深度.显然,对任一时刻t,电磁力F=J×B沿板坯厚度方向上也会呈指数分布.

电磁搅拌在生产中的工艺效果十分明显,国内外学者已对其进行了大量研究.李宝宽等[2]详细分析了电磁搅拌计算模型,并利用旋转磁场计算模型对不同电流、频率和齿宽下的电磁场进行了计算,还详细给出了各参数对电磁力的影响.Fujisaki[3]通过对结晶器内的热传导及凝固坯壳进行数值模拟发现,电磁搅拌能够均匀凝固坯壳并稳定弯月面处的温度. Takatani[4]通过对结晶器内的流场及温度场进行模拟发现,在低拉速下对结晶器内钢水施加电磁搅拌可提高弯月面处的活跃度和温度,且效果与钢水注流的角度相关.上述研究大多采用数值模拟方法,尽管研究结果可定性或半定量地给出结晶器内钢水流场的评估和分析,但由于目前流体力学中关于湍流的理论和计算模型尚有不足,因此难以准确给出结晶器内真实的具有定量意义的流场.

近年来,随着金属液流测速技术的不断进步,已有研究者开始采用金属液物理模拟的方法进行电磁场控制连铸结晶器内金属液流动的实验研究[5-9].基于此,本工作以水银为模拟工质进行行波磁场作用下板坯结晶器内金属流场的模型实验.本实验采用超声多普勒测速仪(ultrasound Doppler velocimetry,UDV)[10]测量电磁场作用下金属液的流速,并结合基于湍流雷诺应力模型的数值模拟,研究行波磁场(电磁搅拌)作用下,结晶器内钢水的流态,由此分析电磁场控流的基本特点和规律.实验结果表明,物理与数值模拟相结合可较清楚地显示在行波磁场(电磁搅拌)作用下,板坯连铸结晶器内金属液的流态和规律,为连铸工艺设计和优化提供直观的参考依据.

1 研究方法

1.1 模型实验方法

本模型实验以某厂板坯连铸机为原型.实验中结晶器模型与生产原型的几何相似比为1∶6,模型几何参数如表1所示.根据相似原理,实验模型与生产原型通过Fr数和St数相等来实现二者之间流场的物理相似.

式中,l为特征长度,g为重力加速度,v为流速,σ为液态金属电导率,B为磁场强度,ρ为液态金属密度.这里,式(3)给出了模型与原型之间流速的相似关系,而式(4)则给出了模型与原型之间磁场的相似关系.

表1 实验模型的基本参数Table 1 Basic parameters of model

本实验中水银和钢水的密度分别为13 600,7 200 kg/m3,黏度分别为1.523×10-3,5.5× 10-3Pa·s,电导率分别为1.01×106,7.14×105S.由此计算可得：

式中,下标p和m分别表示生产原型和实验模型.

模型实验装置(见图1(a)),包括中间包、浸入式水口、不锈钢制结晶器模型、行波磁场发生器和电磁泵—控制阀—流量计—管路循环系统等.实验所用的行波磁场发生器由双向步进电机组成.磁体几何尺寸为1 250 mm×160 mm,在水平方向完全覆盖整个结晶器宽度并向两边延伸,从而保证了结晶器模型中磁场的均匀性.行波磁场频率为50 Hz,搅拌器输入电压为90 V.结晶器模型中行波磁场分布采用CT3-A特斯拉计进行测试,所得结果如图2所示.实验铸速为0.53 m/min,相当于生产中常用的连铸速度1.3 m/min.

实验中的系统坐标如图1(b)所示,分别以距结晶器厚度中心面±9 mm(相应地距结晶器的前壁面或后壁面6 mm)的宽面平行面与金属液面的交线为x1轴和x2轴,以宽面平行面的中心线为y1轴和y2轴.这样,在实验中所测量的流速为结晶器模型内部(x1,y1)和(x2,y2)平面内的水平和竖直流速.在该坐标平面内沿结晶器两侧的窄面分别自上而下安置7个超声波传感器,用以测量结晶器模型内水银的水平流速,其中最上方的传感器位于液面下5 mm处,其余各传感器以30 mm间距依次向下排布;而在金属液面上,于浸入式水口左右两侧各安置9个传感器,用以测量结晶器模型内水银的竖直流速,其中最外侧的传感器位于距结晶器窄面7.5 mm处,其余各传感器以10 mm间距依次向水口方向排布.

图1 实验装置及测速位置示意图Fig.1 Schematic of physical simulation of metal fl ow in mold

图2 实测的行波磁场分布Fig.2 Distribution of travelling magnetic fi eld measured in experiment

1.2 数值模拟方法

电磁搅拌下的结晶器内金属流场呈现强湍流特征,比普通连铸或电磁制动下要复杂得多.因此,为弥补物理模拟实验中超声波传感器数量有限,以及各传感器之间间距较大使流速的探测点较为稀疏的不足,本工作在模型实验流场物理实测的基础上,以模型实验的流场为对象,并以实验实测的流速分布为校正基准进行了数值模拟,最终细化并获取了全域的宏观流场.

考虑到几何模型的对称性,并假设结晶器内流场关于结晶器水口中心线对称分布,本工作在计算区域上采用半幅模型,与实验模型中结晶器的右半部对应.在三维数值模型中,x和y坐标轴方向与实验模型的设定一致,并增加了结晶器厚度方向上的坐标轴(z轴).结晶器厚度中心面为z=0平面,z=±9 mm平面则为测速面.

此外,湍流模型采用雷诺应力模型(Reynolds stress model,RSM),该模型对雷诺时均方程中的雷诺应力直接建立微分方程并进行求解,能够反映湍流的各向异性特征[11].受篇幅所限,此处不列出相关的流动控制方程(连续方程、动量方程、雷诺应力模型输运方程).需要说明的是,RSM输运方程包含2个与传统k-ε模型不同的辅助方程(k,ε方程)：

式中,C1=1.44,C2=1.92,湍动能k与耗散率ε的湍流普朗特数分别为σk=0.82,σε=1.0.

计算中将电磁力F=J×B作为源项体积力参与流场计算,同时忽略钢水在结晶器中的凝固行为.由此,边界条件以如下方式设定.

(1)将钢水入口注流流速视为均匀分布,并由拉坯速度衡算确定,此处为0.517 m/s.钢水入口处的k和ε计算如下：

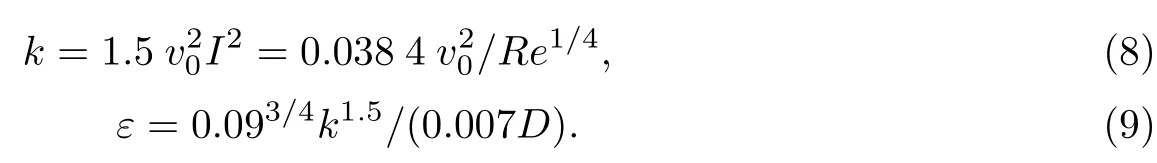
式中,D为水口内径.

(2)将结晶器出口处钢水边界设为压力出口.设回流湍动能和回流耗散率的初值为10-5,当计算达到稳定后,再根据出口处回流值进行调整直到稳定.

(3)对于钢水液面,沿法线方向的速度分量为0,其余变量沿该法线方向的梯度为0.

(4)对于结晶器壁面,在结晶器对称面的法向上,各变量梯度为0.结晶器内壁为无滑移边界条件,靠近壁面各节点处的分量由标准壁面函数来确定.

2 结果与讨论

2.1 行波磁场对结晶器内靠近前后壁面处金属流场的影响

图3和4分别为普通连铸(无电磁搅拌)和施加行波磁场(电磁搅拌)条件下,结晶器模型中靠近前后壁面(x1,y1)和(x2,y2)平面内流场的模型实验实测和数值模拟结果.由图3可见,普通连铸下结晶器内的宏观流场为常规流态,与结晶器中面的流场基本一致,即钢水自水口进入结晶器,流向两侧窄面并分流成上下回流;而在行波磁场(电磁搅拌)下结晶器内的宏观流场发生了很大改变,在电磁力的推动下,金属液在结晶器内形成全区域的水平环流.由图4的三维模拟结果可见,金属液在结晶器内的流动特征如下：金属液自水口出流,但流动的对称性发生改变,出流趋向与电磁力同向的一侧,流速增大且方向趋于水平,而上部回流被驱赶到靠近窄边弯月面的位置;此后,一部分液流冲向结晶器下部,并在电磁力的作用下,在整个结晶器宽面的电磁搅拌区及其下方靠近搅拌区的部分区域中形成一个全域的环流,表现为在水口出流与电磁力方向一致的区域中形成下降流,而在水口出流与电磁力反向的区域中形成上升流.同时,数值模拟结果显示,在水口右侧出口附近有一个小范围的回流形成.从上述流态分析来看,这会增大水口出流与电磁力反向一侧结晶器液面的波动幅度.在电磁搅拌及其附近区域,金属液流形成了覆盖整个结晶器宽面的环流,其中心在电磁搅拌区的下方,这会导致该处金属液形成封闭流,不利于电磁搅拌器下方区域中夹杂物的上浮.由此可见,在电磁搅拌作用下,结晶器内的宏观流场发生了剧烈改变,尽管搅拌区内的夹杂物由于易发生碰撞等行为而长大、上浮,但若夹杂物在搅拌区内未能上浮而进入搅拌区下方的流场,则会因该处流场呈自封闭流态而使夹杂物较难上浮,这是在设计连铸电磁搅拌装置和工艺时必须要注意的问题.

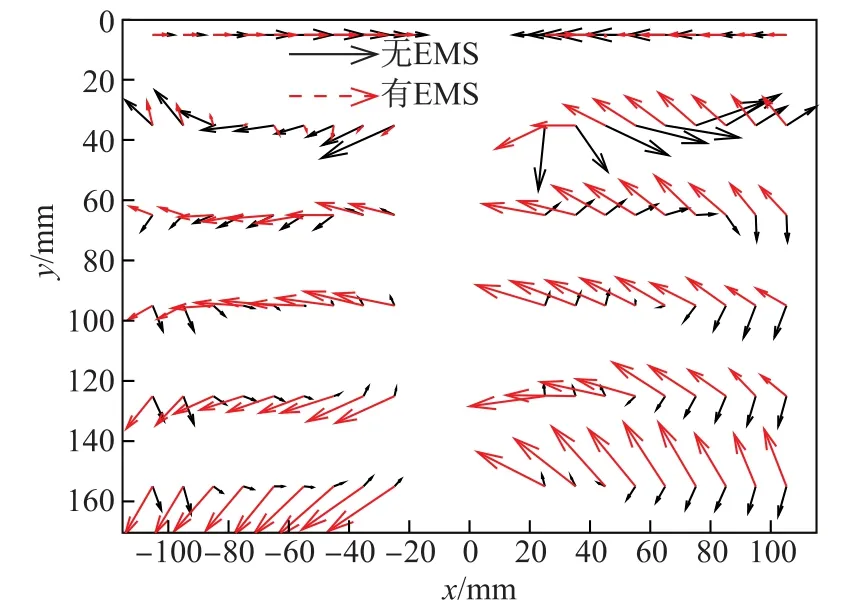
图3 有、无电磁搅拌下结晶器模型内靠近前后壁面处水银流场的实测结果Fig.3 Measured velocity of liquid metal in the mold model with or without EMS

图4 有、无电磁搅拌下结晶器模型内靠近前后壁面处水银流场的数值模拟结果Fig.4 Computational velocity of liquid metal in the mold model with or without EMS

2.2 行波磁场对结晶器中面流场的影响

图5为有、无行波磁场(电磁搅拌)下,板坯结晶器厚度中面(z=0)流场的数值模拟结果.可见,行波磁场(电磁搅拌)下板坯结晶器中面流场(见图5(b))较普通连铸(无电磁搅拌)下(见图5(a))显得紊乱,面上各环流的位置及流态等规律性被削弱.从流速分布上看,该平面内的物流无法平衡.这说明在结晶器中面(几何对称面)上,电磁搅拌作用下的流场也是三维的,与之相对应的普通连铸下的流场则是二维的,这是电磁力驱动结晶器前后层面的金属液流朝相反的方向加速并积累的结果.

图5 有、无电磁搅拌下结晶器中面流场的数值模拟结果Fig.5 Computational velocity in mid-plane of the mold model with or without EMS

2.3 行波磁场对结晶器内液面流场和液面波动的影响

图6为行波磁场(电磁搅拌)下结晶器液面流场的数值模拟结果.可见,由于电磁力的作用,在靠近结晶器后壁面处产生了流向窄面的逆向液流,这与图2的实测结果是一致的.在连铸过程中,液面区域的电磁搅拌有利于该处物质和热量的交换,进而有利于融渣.

图7为模型实验中实测的有、无行波磁场(电磁搅拌)下,结晶器内的液面波动情况.由图3可知,在电磁搅拌作用下,结晶器液面的流速分布由普通连铸(无电磁搅拌)下的对称状态变为不对称状态,此时结晶器一侧液面的水平流速会明显上升,而图7显示了该侧液面的波动幅度有所增大.由图7可见,普通连铸(无电磁搅拌)下结晶器液面水口两边的波动幅度是基本对称的,平均波动幅度(波高)分别为2.41和2.82 mm;而在行波磁场(电磁搅拌)下,结晶器右侧液面的平均波动幅度达到8.2 mm,左侧液面的平均波动幅度则为4.2 mm.显然,本实验中施加行波磁场(电磁搅拌)使结晶器水口两侧的液面波动幅度分别比普通连铸(无电磁搅拌)下增大了0.75倍和1.90倍.可见,施加行波磁场(电磁搅拌)使局部液面波动明显加剧.尽管施加行波磁场(电磁搅拌)有利于融化钢水表面覆盖的保护渣,但液面波动过大也易产生卷渣现象,尤其在高连铸速度工况(钢水液面流速大)下,易使液面流动紊乱,导致铸坯产生夹杂、热裂等凝固缺陷.

图6 行波磁场(电磁搅拌)下结晶器液面流场的数值模拟结果Fig.6 Computational velocity in meniscus with EMS

图7 有、无电磁搅拌下结晶器内液面的波动幅度Fig.7 Wave height of meniscus in the mold model with and without EMS

3 结论

(1)在电磁搅拌作用下,结晶器的搅拌区内形成了与电磁力方向一致的水平环流,使水口两侧的流场呈现出明显的非对称性,出流趋于与电磁力同向.在结晶器内水口出流与电磁力同向的一侧,液面流速增大且方向趋于水平,上部回流被驱赶到靠近窄边弯月面的位置.同时,在电磁力的作用下,整个结晶器宽面的电磁搅拌区及其下方靠近搅拌区的部分区域中,形成了覆盖全域的环流.这会导致该区域金属液形成封闭流,不利于电磁搅拌器下方夹杂物的上浮.

(2)相比于普通连铸,电磁搅拌作用下的结晶器中面流场更显紊乱,原有标志性的上下环流被破坏,取而代之的是三维强湍流流态.

(3)行波磁场(电磁搅拌)下结晶器内金属液面形成水平环流,液面波动幅度增大,且水口出流与电磁力反向一侧的波动幅度更大.本实验中行波磁场(电磁搅拌)下结晶器水口两侧的液面波动幅度分别比普通连铸(无电磁搅拌)下增大了0.75倍和1.90倍.

[1]毛斌,陶金明,李晋,等.板坯连铸结晶器电磁控制流动技术[J].连铸,2006(6)：32-37.

[2]李宝宽,邓康.钢连铸电磁搅拌技术的理论分析[C]//特钢连铸技术研讨会论文集.2007：120-125.

[3]FUJIsAKI K.In-mold electromagnetic stirring in continuous casting[J].IEEE Trans Indus Appl, 2001,37(4)：1098-1104.

[4]TAKATANI K.E ff ects of electromagnetic brake and meniscus electromagnetic stirrer on transient molten seel fl ow at meniscus in a continuous casting mold[J].ISIJ Int,2003,43(6)：915-922.

[5]于湛,张振强,任忠鸣,等.板坯电磁制动结晶器内流体流动的研究[J].金属学报,2010,46(10)：1275-1280.

[6]于湛,周月明,任忠鸣.磁感应强度对高速流动控制结晶器内金属液流动的影响[J].上海金属,2011, 33(6)：36-40.

[7]王寅,张振强,于湛,等.射流型磁场排布方式控制结晶器内液流的实验研究[J].金属学报,2011, 47(10)：1285-1291.

[8]王敏,贾皓,张振强,等.电磁制动下板坯结晶器内金属流动的物理模拟[J].上海金属,2011,33(6)：41-45.

[9]于湛,雷作胜,贾洪海,等.液态金属流速的测量技术[J].上海金属,2007,29(2)：54-58.

[10]JIA H,ZHANG Z Q,CHANG T X.Study on fl ow in mold with EMBr in slab continuous casting[J]. J Iron Steel Res Int,2012,19(S1)：1001-1005.

[11]ZHANG X W,JIN X L,WANG Y.Comparison of standard k-ε model and RSM on three dimensional turbulent fl ow in the SEN of slab continuous caster controlled by slide gate[J].ISIJ Int, 2011,51(4)：581-587.

本文彩色版可登陆本刊网站查询：http：//www.journal.shu.edu.cn

In fl uence of traveling magnetic fi eld on fl ow in continuous casting of slab

TU Ting-sheng,DENG Kang,ZHANG Zhen-qiang,REN Zhong-ming
(Shanghai Key Laboratory of Modern Metallurgy and Materials Processing,School of Materials Science and Engineering,Shanghai University,Shanghai 200072,China)

This paper presents a mercury model experiment and coupling numerical simulation with Reynolds time-average model on molten metal fl ow in the mold of continuous casting of slab.The purpose is to study the in fl uence of a traveling magnetic fi eld(electromagnetic stirring)on the metal fl ow in the mold.The result shows that,in the mold, the stirring force from the traveling electromagnetic fi eld makes the molten metal form a horizontal circum fl uence,leading to destroy of the originally regular circum fl uence.In the whole mold,the fl ow is three dimensional and non-symmetrical.Furthermore,the traveling magnetic fi eld strengthens fl uctuation of meniscus.The fl uctuation is stronger on the side where the nozzle fl ow is opposite to the electromagnetic force.

continuous casting of slab;traveling magnetic fi eld;electromagnetic stirring; molten metal fl ow;Reynolds stress model

TF 777.1

A

1007-2861(2015)01-0020-08

10.3969/j.issn.1007-2861.2014.04.019

2015-01-16

国家自然科学基金资助项目(50674066)

邓 康(1958—),男,教授,博士生导师,博士,研究方向为电磁冶金.E-mail：dengk2000@163.com