Distributed Model Predictive Control with Actuator Saturation for Markovian Jump Linear System

Yan Song,Haifeng Lou,and Shuai Liu

Distributed Model Predictive Control with Actuator Saturation for Markovian Jump Linear System

Yan Song,Haifeng Lou,and Shuai Liu

—This paper is concerned with the distributed model predictive control(MPC)problem for a class of discrete-time Markovian jump linear systems(MJLSs)subject to actuator saturation and polytopic uncertainty in system matrices.The global system is decomposed into several subsystems which coordinate with each other.A set of distributed controllers is designed by solving a min-max optimization problem in terms of the solutions of linear matrix inequalities(LMIs).An iterative algorithm is developed to achieve the online computation.Finally, a simulation example is employed to show the effectiveness of the proposed algorithm.

Index Terms—Distributed model predictive control(MPC), actuator saturation,Markovian jump linear system(MJLS), linear matrix inequality(LMI).

I.INTRODUCTION

M ANY real systems,such as solar thermal central receivers,economic systems,and manufacturing systems, are subject to random abrupt changes in their inputs,internal variables and other system parameters[1].It is difficult to describe the above systems using conventional linear timeinvariant systems.However,Markovian jump linear systems (MJLSs)[2-4]have been put forward to successfully solve this problem.Therefore,in the past decades,MJLSs have received considerable interest,and we can find examples in[5-7]. Since it is often difficult to identify exact model parameters, the control of MJLSs with uncertainty in model parameters has been taken an important consideration of[1].With the increasing development of computer science and technology, discrete-time MJLSs has been applied in a receding horizon control scheme[8].

Model predictive control(MPC),which is also called receding horizon control,has drawn extensive attention from both theoretical and industrial communities with its advantages in processing large-scale,constraint,multi-variable pro-cesses.Nowadays,the systems to be handled are increasingly complex[9].It is pretty difficult to control these systems with a centralized MPC control strategy due to the computational complexity and communication bandwidth limitations[10].Recently,the distributed MPC framework where each subsystem is controlled by an independent controller has been increasingly focused on for its flexibility of system structure, error-tolerance,less computational efforts and no requirements for global information[11].In distributed MPC algorithm,we divide the global system into several subsystems and each subsystem exchanges information with others via network. In[12],Jia et al.provided a communication based on MPC scheme where each subsystem optimized a local cost function and made coordination via communication.Mercang¨oz and Doyle[13]put forward an iterative implementation of a resembling distributed MPC scheme and applied it to a fourtank system.These communication based on distributed MPC algorithm only achieved a Nash-optimization[14].A robust distributed MPC algorithm was proposed in[15-16],in which the model uncertain problem was converted into solving a linear matrix inequality(LMI)optimization problem.In[17], Ding addressed the distributed MPC of a set of polytopic uncertain local systems with decoupled dynamics.

Yan Song and Haifeng Lou are with the Department of Control Science and Engineering,University of Shanghai for Science and Technology,Key Laboratory of Modern Optical System,Engineering Research Center of Optical Instrument and System,Ministry of Education,Shanghai 200093, China(e-mail:sonya@usst.edu.cn;lhfbalance@163.com).

Shuai Liu is with the Business School,University of Shanghai for Science and Technology,Shanghai 200093,China(e-mail:liushuai871030@163. com).

In this paper,we propose a distributed MPC algorithm for a class of uncertain discrete-time MJLSs subject to actuator saturation.We use state feedback to ensure the stability of system.Thus,we assume that system states are measurable. We decompose the global system into several subsystems and a min-max distributed MPC strategy is proposed for the polytopic uncertain distributed systems.In order to better reflect the practical system under the networked environment, we consider the MJLSs subject to actuator saturation.At each time step,an MPC algorithm optimizes a cost function, which is associated with the future states and manipulated variables[9]to obtain a control input.In the next time step, a new cost function is formulated and solved based on the new measurements.An iterative algorithm is developed to get sub-optimizations of the neighbor subsystems.

The rest of this paper is organized as follows.Section II describes the problem statement.In Section III,based on the state feedback control law,a distributed MPC algorithm for input-saturated polytopic uncertain systems is proposed.The effectiveness of the proposed approach is illustrated in Section IV with the help of numerical examples.Finally,we give a conclusion to our work in Section V.

Notations.The following notations are used throughout the paper.Rnand Rn×mdenote the n-dimensional Euclidean space and the set of all n×m real matrices,respectively.xi(k+n|k)denotes the state of subsystem i at time k+n,predicted based on the measurements at time k.ui(k+n|k)refers to the predicted control move at time step k+n and ui(k|k) is the control move to be implemented at time step k.‖x‖2denotes the Euclidean norm of the vector x.I and 0 denote the identity matrix and zero matrix of compatible dimension, respectively.E{x}stands for the expectation of stochastic variable x.G＞0 means matrix G is real symmetric and positive definite.The symbol“∗”denotes the symmetric part in a symmetric matrix.

II.PROBLEM STATEMENT

Consider a certain discrete-time MJLS subject to actuator saturation described by

where x(k)∈Rnxis the system state;u(k)∈Rnuis the control input;y(k)∈Rnyis the controlled output;rkis the system mode.The initial state is x0,and the initial mode is r0. According to the definition in[6],we can see the true“state”involves in two parts:the continuous parts,i.e.,x(k),and the discrete part,i.e.,the mode rk.For a fixed mode rk,the MJLS is a linear time-varying system in essence.In another word, mode rk,i.e.,the present mode,is known,while the next mode rk+1is stochastic and uncertain.Let rk(k∈[0,N])be a Markov chain taking values in a finite state space M={1, 2,...,S}with transition probability given by

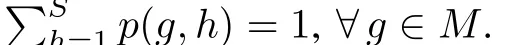
It is assumed that for∀rk∈M,A(ξ)(rk),B(ξ)(rk)and C(ξ)(rk)are unknown matrices which are involved in a convex polyhedral set Ω(rk)described by L vertices

where Co{}refers to the convex hull,that is,

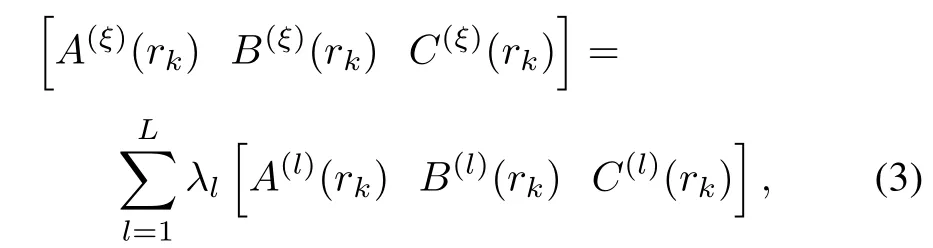
We decompose the global system into M subsystems and design the corresponding distributed MPC controllers for them.In the following,we give some assumptions for our discussion.

Assumption 2.In this paper,we neglect the effect of packet loss,packet disorder,time delay,etc.

Thus,the distributed polytopic uncertain system models with actuator saturation by decomposition can be described by

Remark 3.Owing to the limitation of the communication bandwidth,the large information-carry packets may be saturated at actuator node.The actuator saturation is an essential issue in the control community,which leads to nonlinearity of the system and has being focused on in recent years such as in[19].In this paper,we discuss the distributed MPC problem for MJLs with actuator saturation.

The aim of this paper is to find a set of state feedback laws as follows:

in order to stabilize the system.

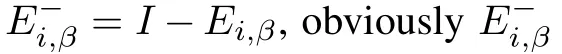
III.MAIN RESULTS

A.Controller Design

In this section,the stability of the distributed polytopic certain discrete-time MJLS subject to actuator saturation is discussed,and the corresponding distributed MPC controllers are designed.To discuss a distributed MPC problem under the state feedback control,an upper bound on a robust performance objective is minimized for every subsystem defined by (4)-(6).The min-max problem on the objective is solved as follows:

where Qi＞0 and Ri＞0 are symmetric weighting matrices. With the overall cost function taken into consideration in(7), it becomes a cooperative distributed MPC algorithm subject to actuator saturation.Applying the state feedback law(6)to (4)results in the following closed-loop system:

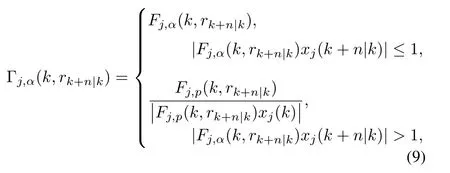
where α=1,...,mi.Γj,α(k,rk+n|k)stands for the α-th row of Γj(k,rk+n|k),Fj,α(k,rk+n|k)refers to the α-th row of Fj(k,rk+n|k).Then,we have

In the sequel of the paper,for presentation convenience, we denote each possible rk+n|k=p(p∈M).The closedloop system(8)by applying unsaturated-input couplings can be rewritten as follows:

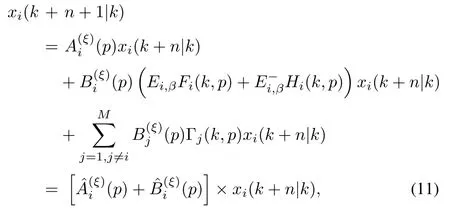
where i=1,...,M,n≥0,p∈M.According to the stochastic switching of the discussed system(4)in certain given modes,the system should be a stochastic one and then the quadratic functions Vi(k+n|k)should be stochastic.Thus, during the stability analysis,we should take the expectation of the quadratic functions Vi(k+n|k).To derive an upper bound on(7),we impose the following robust stability constraints

hold.Then the gain matrix

and the upper bound of the optimization problem is ρi(k), where

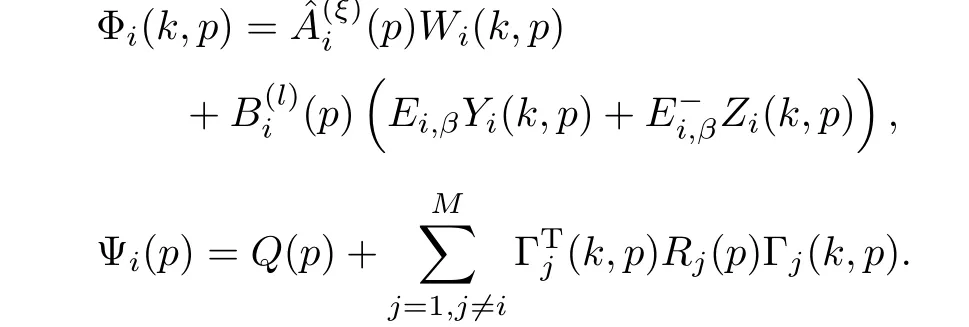
Proof.The difference of Vi(k+n|k)along system(11)can be calculated as follows:

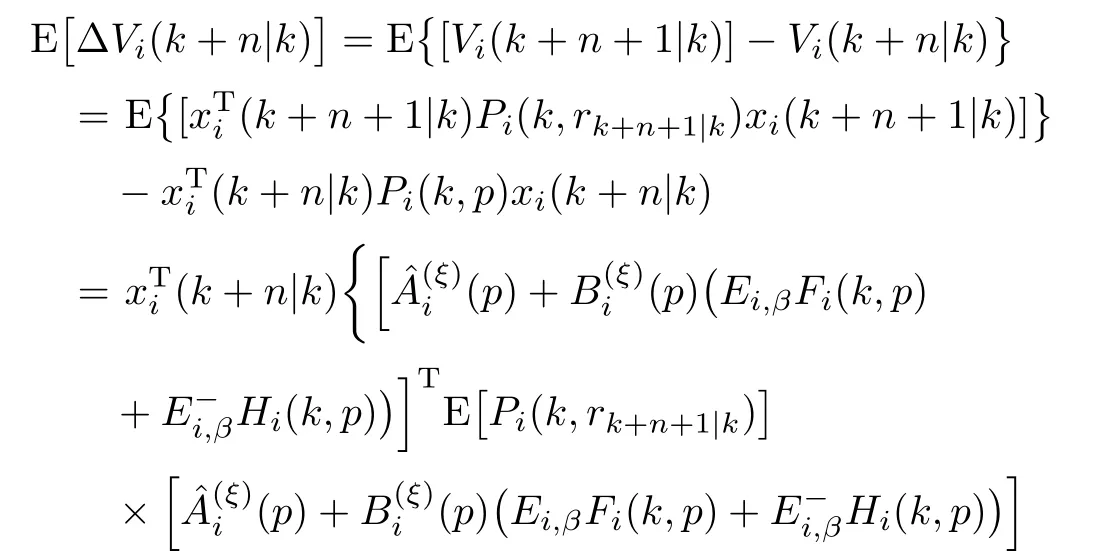
Furthermore,(12)can be reformulated as follows:

By applying(9)into(16),we can get following inequality:

According to(2),it is clear that

Then combining(15)and(17),we can obtain the following inequality:

According to(5),the above inequality is satisfied if and only if

Then,inequalities(20)can be further simplified by multiplying with ρi(k)

By using the Schur complement,if LMI(13)holds,the above inequality will be satisfied.

In the following,based on the robust stability constraints (12),an upper bound on the worst-case infinite horizon(7) can be obtained.Firstly,taking the expected values on the both sides of(12)conditional on the information available at time instant k,the following inequality holds

Then,summing up the above inequality from n=0 to∞on both sides,we have

Because the robust performance objective function Ji(k) should to be finite,we must have xi(∞|k)=0,which leads to Vi(∞|k)=0,

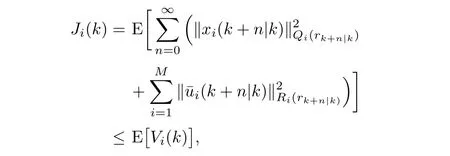
that is

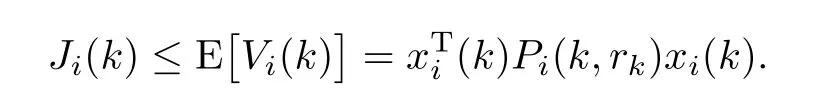
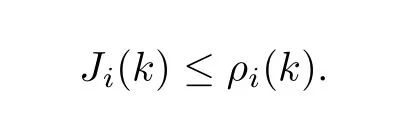
We can see that ρi(k)is an upper bound on the expected cost function.□

where zi,α(k)=Wi(k)hi,α(k).

Next,we will minimize upper bound to approximately minimize the worst-case infinite horizon expected cost function. Now,we are ready to present the unconstrained distributed MPC of MJLSs with polytopic uncertainties in terms of a minimization problem at each time instant k as follows:

In the following theorem,we will discuss the feasibility and stability of(23).

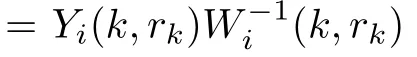
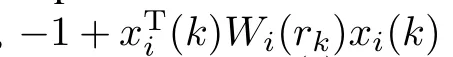
B.Iteration Algorithm

Notice that there are couplings in LMIs(13)when solving problem(23).We propose an iterative distributed MPC algorithm in this section.

Iterative distributed MPC algorithm subject to actuator saturation of i-th subsystem is as follows:

Step 1.At time step k=0,set an initial feedback law Fi(0,rk),i=1,2,...,M.

Step 2.At time step k,all subsystems exchange their local states measurements and initial feedback law Fi(k,rk)via communication,set iteration t=1 and Fi(k,rk)=Fi(0,rk).

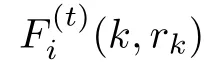
Step 4.The optimal scheme ui(k)=Fi(k,rk)xi(k)is applied to the corresponding subsystems.Set the time interval k=k+1 and go back to Step 2.

Iteration algorithm is solved in parallel for all subsystems, thus the feedback laws can be obtained at a same time.In this way,the computational time can be saved by distributed MPC algorithm.

Lemma 4[15].For cooperative distributed MPC algorithm, the performance indices ρ1(k),ρ2(k),...,ρM(k),of subsystems will converge to the centralized problem with the increase of iteration times,which implies

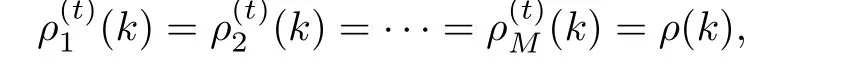
where ρ(k)is the upper bound of centralized MPC at time interval k.

Proof.The proof is similar to[15].For subsystem i,

Similarly for subsystem j,

Remark 4.Lemma 4 tells us that the performance by distributed MPC algorithm can be as good as the performance by centralized MPC algorithm within several iterations.However, the more computational time will be cost with the increase of iteration times.There is a tradeoff between computational time and the performance.In terms of computational time, the distributed MPC presented in this paper can outperform centralized MPC with little performance loss when terminated after a few iterations.

IV.NUMERICAL EXAMPLES

Example 1.Consider the system as follows:

where the system matrices are represented by the following two vertices:

wherer1 andr2 denote Mode 1 and Mode 2,respectively. Assume that the transition probability matrices with polytopic uncertainties can be denoted as

We decompose the global system into two subsystems,each of which has one control input.The actuator saturation is described asσ(u1(k))=sgn(u1(k))min{1,|u1(k)|}andσ(u2(k))=sgn(u2(k))min{1,|u2(k)|}.The proposed distributed MPC algorithm is used to control these two subsystems with initial statex0=[-1,1]Tand weighting matricesQ1=Q2=I2,R1=R2=1.The performance of distributed algorithm is compared with centralized MPC algorithm under the same weighting matrices.

Fig.1 shows the invariant sets obtained by different algorithms at the first sampling step.It can be seen that the proposed distributed MPC algorithm reaches the same invariant set as centralized MPC algorithm after three iterations, which validates the result of Lemma 4.Fig.2(a)presents the upper-bound trends of centralized MPC,subsystems 1 and 2, respectively,from which we find that only after three iterations the upper bound of the subsystems 1 and 2 almost converge to the upper bound of centralized MPC.From Fig.2(b)we can see the upper bound either by centralized MPC or by distributed MPC will converge to zero when the time stepktends to infinite.The comparison of upper bound and computational time between centralized MPC(CMPC)and distributed MPC(DMPC)at the first sampling step is shown in Table I.The distributed MPC algorithm is applied with one single iteration,two iterations and three iterations.From Table

Fig.1.Invariant sets comparison at the first sampling interval.

Fig.2.Upper bounds of centralized MPC and two subsystem.

I,we can see the distributed MPC algorithm only takes 0.92 s after three iterations,which is less than 1.23 s by centralized MPC.Distributed MPC outperform centralized MPC with little performance loss,which validate the results described in Remark 4.

V.CONCLUSION

Thinking of the uncertainty and abrupt changes of system parameters,we present a distributed MPC for MJLSs.By decomposing the system into several subsystems to design the distributed controllers,it can decrease the system complexity and computation cost.In each subsystem,a distributed MPC strategy is proposed.The distributed controller is obtained by solving an LMI optimization problem and an iteration algorithm is developed for making cooperation among subsystems.Due to the consideration of actuator saturation,the main results made in this paper are more practical than those with ideal network connection.In the end,an example illustrates the effectiveness of the proposed distributed MPC algorithm.

TABLE I UPPER BOUND AND CPU TIME COMPARISON BETWEEN CENTRALIZED MPC AND DISTRIBUTED MPC

REFERENCES

[1]Park B G,Kwon W H.Robust one-step receding horizon control of discrete-time Markovian jump uncertain systems.Automatica,2002, 38(7):1229-1235

[2]Sworder D D,Rogers R O.An LQ-solution to a control problem associated with a solar thermal central receiver.IEEE Transactions on Automatic Control,1983,28(10):971-978

[3]Blair Jr W P,Sworder D D.Feedback control of a class of linear discrete systems with jump parameters and quadratic cost criteria. International Journal of Control,1975,21(5):833-841

[4]Boukas E K,Haurie A.Manufacturing flow control and preventive maintenance:a stochastic control approach.IEEE Transactions on Automatic Control,1990,35(7):1024-1031

[5]Costa O L V,Fragoso M D,Marques R P.Discrete-time Markov Jump Linear Systems.London:Springer,2005.

[6]Lu J B,Li D W,Xi Y G.Constrained model predictive control synthesis for uncertain discrete-time Markovian jump linear systems.IETControl Theory and Applications,2013,7(5):707-719

[7]Wei G L,Wang Z D,Shu H S.Nonlinear H∞control of stochastic time-delay systems with Markovian switching.Chaos,Solitons and Fractals,2008,35(3):442-451

[8]Byung-Gun P,Wook H,Jae-Won L E E.Robust receding horizon control of discrete-time Markovian jump uncertain systems.IEICE Transactions on Fundamentals,2001,84(9):2272-2279

[9]Zhang L W,Wang J C,Li C.Distributed model predictive control for polytopic uncertain systems subject to actuator saturation.Journal of Process Control,2013,23(8):1075-1089

[10]Scattolini R.Architectures for distributed and hierarchical model predictive control:a review.Journal of Process Control,2009,19(5): 723-731

[11]Song Y,Fang X.Distributed model predictive control for polytopic uncertain systems with randomly occurring actuator saturation and packet loss.IETControlTheoryandApplications,2014,8(5):297-310

[12]Jia D,Krogh B.Min-max feedback model predictive control for distributed control with communication.In:Proceedings of the 2002 American Control Conference.Anchorage,AK,USA:IEEE,2002,6: 4507-4512

[13]Mercang¨oz M,Doyle III F J.Distributed model predictive control of an experimental four-tank system.Journal of Process Control,2007, 17(3):297-308

[14]Li S Y,Zhang Y,Zhu Q M.Nash-optimization enhanced distributed model predictive control applied to the shell benchmark problem. Information Sciences,2010,170(2-4):329-349

[15]Al-Gherwi W,Budman H,Elkamel A.A robust distributed model predictive control algorithm.Journal of Process Control,2011,21(8): 1127-1137

[16]Al-Gherwi W,Budman H,Elkamel A.Robust distributed model predictive control:a review and recent developments.The Canadian Journal of Chemical Engineering,2011,89(5):1176-1190

[17]Ding B C.Distributed robust MPC for constrained systems with polytopic description.Asian Journal of Control,2011,13(1):198-212

[18]Huang H,Li D W,Lin Z L,Xi Y G.An improved robust model predictive control design in the presence of actuator saturation.Automatica, 2011,47(4):861-864

[19]Hu T S,Lin Z L,Chen B M.Analysis and design for discretetime linear systems subject to actuator saturation.Systems and Control Letters,2002,45(2):97-112

[20]Hu T S,Lin Z L.Control Systems with Actuator Saturation:Analysis and Design.New York:Springer,2001.

Yan Song received the B.S.degree from Jilin University,China,in 2001,M.S.degree from University of Electronic Science and Technology of China in 2005,and Ph.D.degree from Shanghai Jiao Tong University,China,in 2013,respectively.She is now an associate professor at University of Shanghai for Science and Technology.Her research interests include model predictive control,networked control, and sensor networks.Corresponding author of this paper.

Haifeng Lou received the B.S.degree from Henan Polytechnic University in 2009.Now he is a postgraduate student at University of Shanghai for Science and Technology.His research interests include networked control system and model predictive control.

Shuai Liu received the B.S.degree from Lu Dong University,Yantai,China in 2011 and the M.S. degree from University of Shanghai for Science and Technology,Shanghai,China in 2014.She is now a Ph.D.candidate at University of Shanghai for Science and Technology,Shanghai,China.Her research interests include model predictive control and set-membership filtering.

t

October 11,2014;accepted February 9,2015.This work was supported by National Natural Science Foundation of China (61403254,61374039,61203143),Shanghai Pujiang Program(13PJ1406300), Natural Science Foundation of Shanghai City(13ZR1428500),Innovation Program of Shanghai Municipal Education Commission(14YZ083),and Hujiang Foundation of China(C14002,B1402/D1402).Recommended by Associate Editor Yugeng Xi.

:Yan Song,Haifeng Lou,Shuai Liu.Distributed model predictive control with actuator saturation for Markovian jump linear system.IEEE/CAA Journal of Automatica Sinica,2014,2(4):374-381