Decentralized Event-Triggered Average Consensus for Multi-Agent Systems in CPSs with Communication Constraints

Zhaoxia Wang,Minrui Fei,Dajun Du,and Min Zheng

Decentralized Event-Triggered Average Consensus for Multi-Agent Systems in CPSs with Communication Constraints

Zhaoxia Wang,Minrui Fei,Dajun Du,and Min Zheng

—The paper investigates decentralized event-triggered average consensus problem for multi-agent systems in cyberphysical systems(CPSs)with communication constraints.To reduce communication burden and improve the communication ef fi ciency of multi-agent systems in CPSs,event-trigger is distributed at subsystem/agent level.A multi-agent system is then modeled as a reduced dimension hybrid system by taking into account decentralized event-triggered mechanism,communication delays and data dropouts within one framework.Some suf fi cient conditions for average consensus of each agent and an upper bound of communication delay and maximal allowable number of successive data dropouts(MANSD)are obtained,which can conveniently provide the relationship between the triggering parameters,communication constraints and the system stability. Specially,the quantitative relationship between the triggering parameters,MANSD and the system stability is derived.Finally, simulation results are given to illustrate the effectiveness of the proposed method.

Index Terms—Decentralized event-triggered,average consensus,communication constraints,cyber-physical systems(CPSs).

I.INTRODUCTION

CYBER-PHYSICAL systems(CPSs)are a kind of novel complex systems which tightly integrate the dynamics of the physical processes with communication,computation and control(3C)[1].In CPSs,the networks and embedded computers are used to transmit data,process information and control a large number of local physical processes[2].CPSs have been used in some practical systems,e.g.,intelligent transportation,smart grids and intelligent robotic systems[3-4].

Compared with the traditional control system,CPSs have several new features.Firstly,the local physical processes in CPSs are geographically distributed,so CPSs are a kindof typical systems which are composed of many smaller subsystems(also called“agents”).Each agent gathers information through the communication network and makes control decisions with other agents together.Multi-agent systems need to be controlled by distributed cooperative control strategy to ensure the performance of the whole system.One of the key issues of distributed cooperative control for multi-agent systems is distributed(or decentralized)average consensus control problem[5-8].The average consensus problem means to design a network protocol such that,as time goes on,the states of all agents asymptotically reach the average of the initial states[5].

Secondly,communication is one key component of CPSs, which in fl uences the performance of distributed cooperative control for multi-agent systems.However,communication network is not always reliable,so the communication constraints including communication delay and data dropouts are inevitably introduced and may degrade the system performance or even cause the system instability.Some researches focus on the consensus problems with communication delay for fi rstorder[5]or second-order systems[8],having fi xed or switching topology[9].A necessary and suf fi cient condition was derived for multi-agent systems with heterogeneous time delays to achieve average consensus[10].The consensus problem with dynamically changing topologies,time-varying delays and data packet dropouts was also investigated[11].

Thirdly,a large number of data are generated by various sensors which represent the different characteristics of physical processes.However,there exist a large number of redundant data within these data which bring greater pressure to the network transmission.It is necessary to propose an eventtriggered sampling mechanism for multi-agent systems[12-13]as an alternative to traditional time-triggered sampling(i.e.,the fi xed sampling period).Using the event-triggered mechanism, the data can be transmitted only when the triggered condition is satis fi ed,which improves the effective transmission of data by reducing communication network burden.

ConsideringthenewcharacteristicsofCPSsmentioned above,researchers studied decentralized event-triggered controlformulti-agentsystemswithoutcommunication constraints[12],where each agent sends its local information to the network only when the norm of measurement error crosses a certain threshold.With decentralized event-triggered control,the triggered instants were reduced without continuous monitoring the states of neighbors[14].Moreover,the recent researches of observer-based output feedback event-triggered control[15]and leader-following exponential consensus problem with distributed event-triggered control[16]were presented.

Furthermore,there are also some researches about decentralized event-triggered problem with partial communication constraints[17-19].Considering communication delays, the novel event-based scheduling strategy was studied[17], which was considered as the time-dependent function.Considering directed graphs,decentralized event-triggered control of discrete-time heterogeneous multi-agent systems was investigated[18].Considering communication delays and data dropouts,the event-triggered data transmission in distributed networked control systems was examined[19-20].However, how to get the quantitative relationship between communication constraints and system stability for undirected fi xed network is still an open issue.It is very important for system performance of multi-agent systems.

Based on the above observation,the previous research results we focused on were the average consensus problem for multi-agent systems with centralized event-triggered mechanism and only communication delays[21-22].Considering the geographically distributed agent and networked-related nondeterministic issues,the further study in this paper is mainly concerned with decentralized event-triggered average consensus problem for multi-agent systems with communication delays and data dropouts in an undirected network.

The generally used decentralized event-triggered functions in the existing work[12-16],all such functions have the similar form,i.e.,Compared with this form,a different event-triggered mechanism is introduced with the form of.It has several parameters to adjust the event-triggered threshold,thus it is more general.Under the event-triggered mechanism[18-19],we will solve the average consensus problem based on the theoretical framework for multi-agent systems with an undirected,connected network topology as in[9].Furthermore,using the time-delay system model in[10],this paper will present the design of decentralized event-triggered average consensus for continuoustime multi-agent systems with communication delays and data dropouts.

Two main contributions are as follows: fi rstly,under the decentralized event-triggered mechanism,a reduced dimension hybrid system model with communication delay and data dropouts is proposed,where the decentralized event-triggered mechanism,communication delays and data dropouts are taken into account within one framework.Secondly,using reciprocally convex approach and Lyapunov-Krasovskii stability theory,suf fi cient conditions that make all the agents achieve the average consensus asymptotically are presented.Furthermore, the upper bound of communication delay and the maximal allowable number of successive data dropouts(MANSD)can be obtained,which can conveniently provide the relationship between the triggering parameters,communication constraints and the system stability.Specially,the quantitative relationship between the triggering parameters,MANSD and the system stability is derived.

The remainder of the paper is organized as follows.Section II presents the problem statement.System model with decentralized event-triggered mechanism and only communication delays is established in Section III.Section IV presents the proposed approach with decentralized event-triggered mechanism and communication delays.Section V gives the results of decentralized event-triggered mechanism with communication delays and data dropouts.Simulation results are described in Section VI.Section VII concludes the paper.

II.PROBLEM STATEMENT

Supposed that a networked subsystem of CPSs consists ofNagents,and each agent is the single-integrator system with dynamics:

wherexi(t)∈RMdenotes the state(or value)andui(t)∈RMdenotes the control input(or protocol)of thei-th agent. Supposed that agentiis regarded as a nodevi,then the network is de fi ned by the graphGwith the sets of nodesV={v1,...,vN}and edgesE={eij=(vi,vj)}⊆V×V.For an undirected graph with nodesN,the set of neighbors of nodeviis denoted asNi={vj∈V|(vi,vj)∈E}.A=[aij]N×Nis a communication adjacency matrix with nonnegative adjacency elementsaij,whereaii=0 andaij＞0(vj∈Ni). The degree matrix isD=diag{d11,d22,...,dNN},wheredii=PThe Laplacian graph ofGis de fi ned asL=D-A.It can be easily obtained that every row sum ofLis zero and thus 1N=[1,1,...,1]T∈RNis an eigenvector ofLassociated with the eigenvalueλ=0.Therefore,this means that Rank(L)≤N-1.

In this paper,we assume that the undirected graphGis connected.TheGis called connected if and only if there is a path between any two distinct nodes.Furthermore,it is easy to know that the LaplacianLof an undirected graphGsatis fi esL1N=0 and=0.

The consensus problem without communication delays has been studied,and the consensus control protocol was given by[9]

Here with the consensus protocol,each agent consists of a controller,and the dynamics is shown in Fig.1.

Fig.1.Agent with the consensus protocol.

We say the nodes of a network have reached a consensus if and only ifxi=xjfor all.Whenever the nodes of a network are all in agreement,the value of all nodes is called the group decision value.Particularly,for alli,j∈I, if there exists

thenui(t)asymptotically solves the average consensus problem.

In this paper,we discuss the consensus problem with communication delays and the consensus control protocol was given by[10]

In many real multi-agent systems,the control inputui(t) updates its value with fi xed periodh,i.e.,each agent is regularly sampled with periodh,where the monotonically increasing sampling sequence is described by the setM1={0,h,2h,...,kh},k∈N.

This time-triggered sampling(i.e.,the fi xed sampling period)leads to heavy burden of the network.Therefore,it is necessary to propose an event-triggered sampling mechanism, which determines agentisends a message or not to its neighbors through network.With event-triggered mechanism, the broadcast release sequence is described by the setM2=1N.

Remark 1.When the conditionM2⊂M1is obtained, the numbers of sampled data are reduced with event-triggered mechanism,which can reduce communication burden.Specially,ifM2=M1it means all sampled data are transmitted and the event-triggered mechanism becomes a time-triggered scheme.

Considering the unreliability of communication network, the communication delay and data dropouts are introduced. Assumed that only data packet dropouts happen in communication,the successful broadcast release of agentiis characterized by monotonically increasing sequencesM3=2,N.Furthermore,considering communication delays,the successful transmission fi nishing instant of sampled value is described by the setM4=, where thedenotes the time delay at successful transmission instantand is bounded with

Remark 2.If all broadcast release data are successfully transmitted without data dropouts,we have,i.e.,M3=M2.Then only considering communication delays,we can still use the sequence setM4to describe the successful transmission fi nishing instant.

III.SYSTEM MODEL WITH DECENTRALIZED EVENT-TRIGGERED MECHANISM AND ONLY COMMUNICATION DELAYS

From Remark 2,considering event-triggered mechanism and only communication delays,we haveM3=M2.De fi ne the state measurement error of agentias follows:

where=+lh,l∈Z,andei()is the error between the current sampled valuexi()and the latest transmission sampled valuexi().

Then the event-triggered transmission scheme is designed as[18-19]

where 0≤γ＜1 is a given and bounded positive scalar parameter,and Φiis a positive de fi nite matrix.

If the condition(6)is satis fi ed,the current sampled informationxi()is transmitted,orfi(()≤0,i.e.,xi()will not be transmitted.Obviously,the released statesxi()is the subsequences of the latest transmission sampled value,which is denoted byxi().

Remark 3.The event-triggered transmission scheme(6)is decentralized.Agentionly requires its own state measurement error and state value to update the event-triggered instant.Due to different agents,the eventtriggered instants are different.Compared with centralized event-triggered mechanism[22],it is not necessary to require the local and its neighbor information at the same time in order to implement the event-triggered condition.Moreover,the matrix Φiin(6)is a positive de fi nite parameter matrix,which is applied to adjust the weight of the event-triggered threshold. Furthermore,considering the distributed event-triggered functions in[12-16],they all have the similar form ofand can be obtained by de fi ning Φi=Iin(6).Therefore, compared with the event-triggered functions in[12-16],the event-triggered condition in this paper is more general.

The following task is to fi nd the conditions for system (14)to reach average consensus with the event-triggered communication scheme(16).

IV.THE PROPOSED APPROACH

A.Problem Setting

From(21),if the following condition

and betweentkhandtkh+nh(n=1,2,...,l)no control signal is triggered,where Φ=diag{Φ1,...,ΦN},Φ′=γΦ,(nkh)==(U1⊗IM)TΦ(U1⊗IM),and=(U1⊗IM)TΦ′(U1⊗IM).

Remark 5.Under decentralized event-triggered mechanism, to solve the average consensus for system(14)with undirected, connected fi xed network topology,a reduced dimension hybrid system(20)is proposed with decentralized event-triggered mechanism(23).Then,using reciprocally convex approach[24], suf fi cient conditions for average consensus are obtained by a linear matrix inequality(LMI)set.This is proven in the following theorem.

B.Main Results

Theorem 1.Consider a system ofNagents with undirected,connected network topology and uncertain communication delays.For some given positive constantsη1,ηNand 0＜γ＜1,under the decentralized event-triggered mechanism(23),the system(20)is asymptotically stable,if there exist matrixS2∈RM×Mand positive de fi nite matrices Φi∈RM×M(i=1,...,N),P,Qi,Ri(i=1,2)∈RM×M,such that

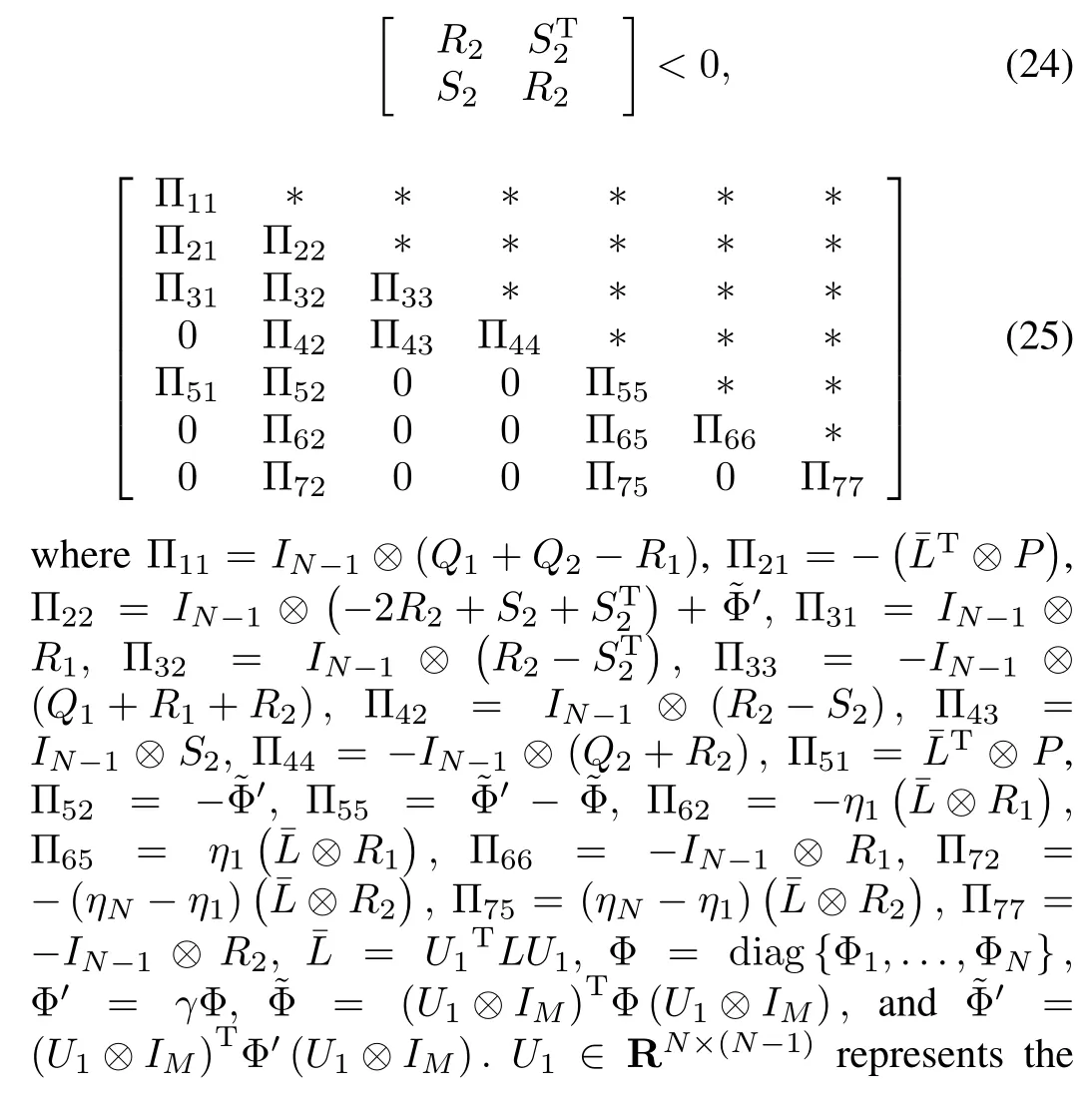
Remark 6.Using the proposed method in Theorem 1,for the given positive constants 0＜γ＜1,an upper boundηN=maxof communication delays can be obtained for all agents.Note that the communication delay of each agent is uncertain and cannot exceed theηN.We also obtain that the maximum sampling timehdoes not exceedηN,where≜h+.When the delay¯τiof each agent is small enough, the upper boundηNgives one possible maximum sampling period.Similarly,when the sampling periodhis small enough, the conservative upper boundηNis the maximum delay.

V.DECENTRALIZED EVENT-TRIGGERED MECHANISM AND MODELING OF MULTI-AGENT SYSTEMS WITH COMMUNICATION DELAYS AND DATA DROPOUTS

If communication constraints include communication delays and data dropouts,it means that not all broadcast release data are successfully transmitted,then we haveM3⊂M2.For data dropouts,they are sometimes modeled as a homogeneous Markov chain[25-26],which cannot give the MANSD.Therefore,considering the MANSD model[19-20],the decentralized event-triggered transmission scheme(6)is changed as

where 0≤σ＜1 and

Compared with scheme(6),the state measurement error of agent in(26)is different and 0＜σ≤δ＜1 is satis fi ed in order to consider the extra communication delays by data dropouts.

Similarly,with decentralized event-triggered transmission scheme(26),the broadcast release instantrik+1his de fi ned by

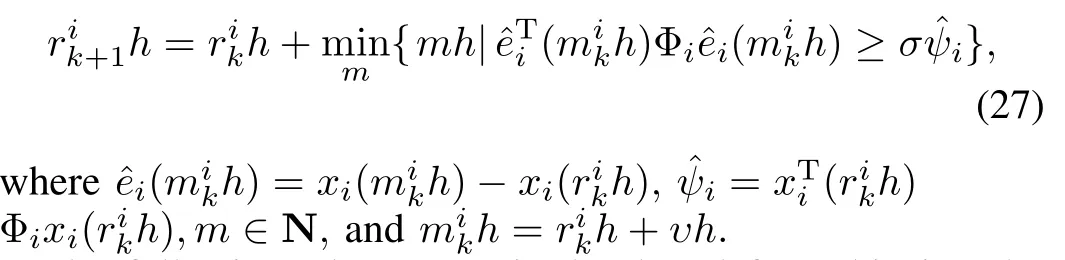
The following Theorem 2 is developed for achieving decentralized event-triggered average consensus with communication delays and data dropouts.

Theorem 2.Consider a system ofNagents with undirected, connected network topology,uncertain communication delays and data dropouts.For some given positive constantsh,η1,ηNandγ,σ,under the decentralized event-triggered mechanism(27),the system(20)is asymptotically stable,if there exist matrixS2∈RM×Mand positive de fi nite matrices Φi∈RM×M(i=1,...,N),P,Qi,Ri(i=1,2)∈RM×M,such that(24)and(25)hold,and the MANSD de fi ned bydMANSDsatis fi es

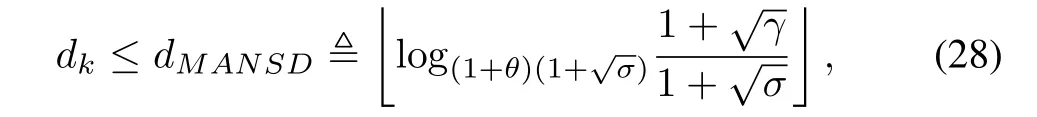
whereθ=and⎿Δ」gives the largest integer smaller than or equal to Δ.

The proof of Theorem 2 is presented in Appendix B.

Remark 7.Theorem 2 can conveniently provide the relationship between triggering parameters,communication constraints and system stability,Specially,the quantitative relationship between triggering parameters,MANSD and system stability is derived.Therefore,considering the given time delaysη1,ηNanddMANSDtogether,the parametersγ,σ,Φiin the event-triggered mechanism can be obtained using the proposed approach.

Algorithm 1 to get the parameters is given here:

Algorithm 1.

Step 1.For the given time delayηN,setγ=γ+µand the step sizeµ=µ0,whereµ0is a speci fi ed constant and small enough and the initial value ofγis set to 0.

Step 2.Based on LMI approach,the feasible solutions that satisfy the matrix inequalities(24)and(25)are obtained.If the feasible solutions can be found,then go to Step 3.Otherwise, go back to Step 1.

Step 3.Using LMI approach,the corresponding Φiis found. For the given sampling periodh,dMANSDand the currentγ, the maximumσ(γ,dMANSD)is obtained under the condition (28).Ifσ(γ,dMANSD)≤0,return to Step 1.

Step 4.Go to Step 1 for another value ofγandσ,untilγ≥1 the search is stopped and the maximumγis found.

VI.NUMERICAL EXAMPLE

To verify the effectiveness of proposed method,we consider an undirected and fi xed network of fi ve agents[17],where each agent can represent a mobile robot in a simple CPS consisting of fi ve mobile robots and is geographically distributed.The communication graphGof the undirected and fi xed network is shown in Fig.2.It has connected digraph with 0-1 weights andxi(t)∈R2is the state vector of agenti.The initial conditions of each agent are set asx1(0)=[-0.5,-0.6]T, x2(0)=[-1,-1.2]T,x3(0)=[3,3]T,x4(0)=[-3,-2.8]T, x5(0)=[1.5,1.6]T.

Fig.2.Communication graphGof the multi-agent system.

In the following,in order to discuss the average consensus problem with decentralized event-triggered mechanism and constraints in CPS,the two cases are analyzed.

1)With decentralized event-triggered mechanism and only communication delays,setγ=0.40,η1=0 andh=0.01. Using Theorem 1,maximum allowable delayηN=0.054 is gained.WithηN=0.05,the state trajectories of fi ve agents are shown in Fig.3.It is seen each component of state vector asymptotically achieves average consensus fort∈[0,6).

Fig.3.State trajectories of agents withγ=0.40,η1=0,ηN= 0.05.

The effectiveness of event-triggered mechanism becomes clear in Fig.4,which shows that the sampling frequency of each agent is remarkably reduced.The speci fi c total eventtriggered instants of each agent are shown in Table I.

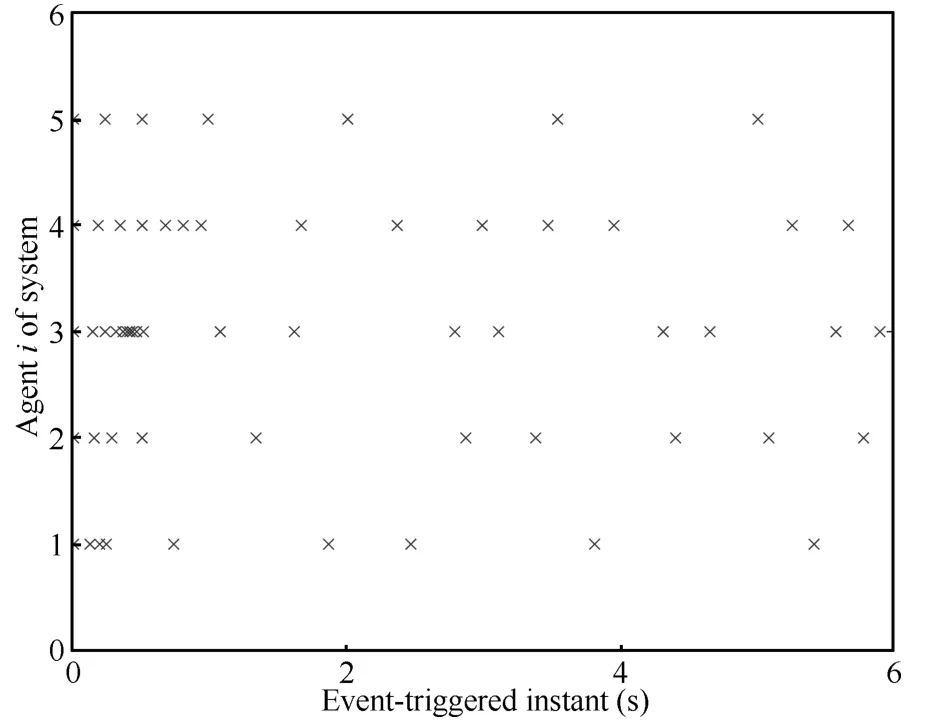
Fig.4.Event-triggered instants of each agent withγ=0.40,η1= 0,ηN=0.05.

TABLE I TOTAL EVENT-TRIGGERED INSTANTS OF EACH AGENT (t∈[0,6))

Remark 8.Note that the numerical example has been used in[17],where the time-dependent trigger conditions with exponentially decreasing thresholds on the measurement errors can guarantee asymptotic convergence to average consensus.However,it is seen from Fig.3 that the system has achieved a faster asymptotic convergence speed to average consensus by using the proposed method.Moreover,compared with our previous work of the centralized event-triggered mechanism[22],the decentralized event-triggered mechanism in this paper only requires its own local measurement error and the current sampled-data to update the event-triggered instant and no longer requires the global information.Therefore, the total number of decentralized event-triggered instants of each agent are different from the centralized event-triggered instants.Moreover,due to uncertainty of the communication delays,the results of each simulation in Fig.4 and Table I are not identical.

2)Considering decentralized event-triggered mechanism with communication delays and data dropouts,setη1=0 andh=0.01.If differentηNanddMANSDare given,based on Algorithm 1,the different maximumγ,σare obtained which are listed in Table II.

From Table II,the simulation results have shown the quantitative relationship between triggering parameters and MANSD.With the allowed MANSD,the values of triggering parametersγandσcannot exceed the maximum values in Table II.We also found that the maximum allowable delay decreases with the increasing of triggering parameterγ.

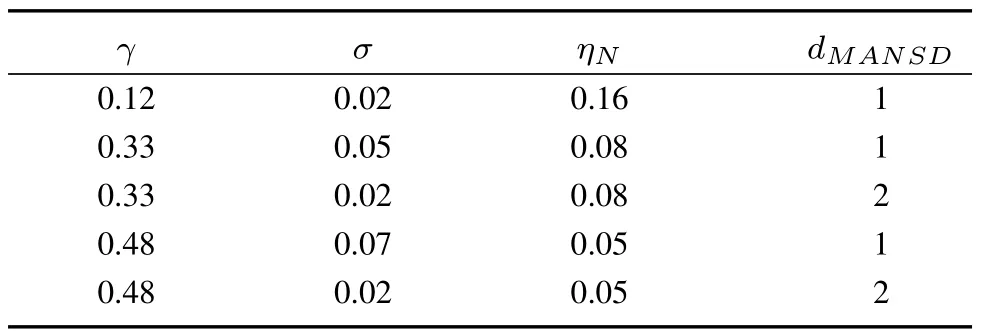
TABLE IIdMANSDWITH DIFFERENTγ,σ

Forη1=0,ηN=0.10,γ=0.10,σ=0.02,h=0.01 anddMANSD=1,the event-triggered instants,successful broadcast release instants and state trajectories of Agent 1 are shown in Fig.5.It shows that,with data dropouts,the successful broadcast release instants are less than the event-triggered instants and Agent 1 asymptotically achieves average consensus. Due to the uncertain communication delays,the successful broadcast release instants are not entirely included in eventtriggered instants.

VII.CONCLUSION

Fig.5.Event-triggered instants,successful broadcast release instants and state trajectories of Agent 1 with time delay and data dropouts.

The decentralized event-triggered average consensus problem for multi-agent systems in CPSs with communication delays and data dropouts has been investigated in this paper. Considering the communication and control characteristics of CPSs,the multi-agent systems are modeled as a reduced dimension hybrid system with decentralized event-triggered mechanism,communication delays and data dropouts.Some suf fi cient conditions for average consensus are presented,and an upper bound of time delay and MANSD are derived. Furthermore,due to CPSs are the complex systems of 3C, how to solve decentralized event-triggered mechanism with computation issue is another important direction in the future.

APPENDIXA PROOF OFTHEOREM1

Based on the system(20),we have constructed a Lyapunov-Krasovskii functional candidate as

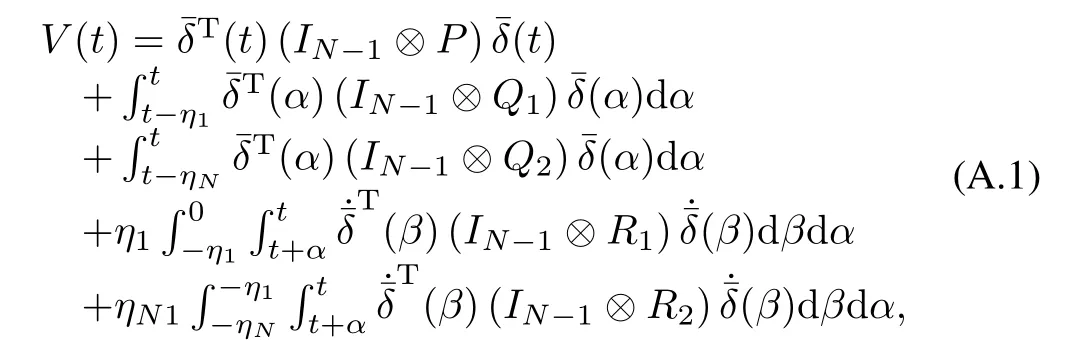
whereP,Q1,Q2,R1,R2∈RM×Mare positive de fi nite matrices andηN1=ηN-η1.

The derivative of(A.1)with respect totis

De fi nition 1.

Since betweentkhandtkh+ih,no control signal is triggered,the condition(A.3)is satis fi ed,then

Then,by Schur complement formula,the matrix inequality (A.5)is equivalent to(25).□

APPENDIXB PROOF OFTHEOREM2

Inequality(B.9)ensures the condition(14)in the Theorem 1,this reveals that Theorem 2 can be derived from Theorem 1 if the the communication scheme(27)is applied.□

REFERENCES

[1]Rajkumar R.A cyber-physical future.Proceedings of the IEEE,2012, 100:1309-1312

[2]Wen Jing-Rong,Wu Mu-Qing,Su Jing-Fang.Cyber-physical system.Acta Automatica Sinica,2012,38(4):507-517(in Chinese)

[3]Liu J L,Zheng Y,Stojmenovic I.Receiver consensus:on-time warning delivery for vehicular ad-hoc networks.IEEE Transactions on Emerging Topics in Computing,2013,1(1):57-68

[4]Derler P,Lee E A,Vincentelli A S.Modeling cyber-physical systems.Proceedings of the IEEE,2012,100(1):13-28

[5]Li T,Fu M Y,Xie L H,Zhang J F.Distributed consensus with limited communication data rate.IEEE Transactions on Automatic Control, 2011,56(2):279-292

[6]Sun F L,Guan Z H,Ding L,Wang Y W.Mean square averageconsensus for multi-agent systems with measurement noise and time delay.International Journal of Systems Science,2013,44(6):995-1005

[7]Cao Y C,Yu W W,Ren W,Chen G R.An overview of recent progress in the study of distributed multi-agent coordination.IEEE Transactions on Industrial Informatics,2013,9(1):427-438

[8]Huang Q Z.Consensus analysis of multi-agent discrete-time systems.Acta Automatica Sinica,2012,38(7):1127-1133

[9]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533

[10]Sakurama K,Nakano K.Necessary and suf fi cient condition for average consensus of networked multi-agent systems with heterogeneous time delays.International Journal of Systems Science,2015,46(5):818-830

[11]Sun Y G,Wang L.Consensus of multi-agent systems in directed networks with nonuniform time-varying delays.IEEE Transactions on Automatic Control,2009,54(7):1607-1613

[12]Dimarogonas D V,Frazzoli E,Johansson K H.Distributed eventtriggered control for multi-agent systems.IEEE Transactions on Automatic Control,2012,57(5):1291-1297

[13]Meng X Y,Chen T W.Event based agreement protocols for multi-agent networks.Automatica,2013,49(7):2125-2132

[14]Garcia E,Cao Y C,Yu H,Antsaklis P,Casbeer D.Decentralised eventtriggered cooperative control with limited communication.International Journal of Control,2013,86(9):1479-1488

[15]Zhang H,Feng G,Yan H C,Chen Q J.Observer-based output feedback event-triggered control for consensus of multi-agent systems.IEEE Transactions on Industrial Electronics,2014,61(9):4885-4894

[16]Zhou B,Liao X F,Huang T W,Chen G.Leader-following exponential consensus of general linear multi-agent systems via event-triggered control with combinational measurements.Applied Mathematics Letters, 2015,40:35-39

[17]Seyboth G S,Dimarogonas D V,Frazzoli E,Johansson K H.Eventbased broadcasting for multi-agent average consensus.Automatica, 2013,49(1):245-252

[18]Yin X X,Yue D,Hu S L.Distributed event-triggered control of discretetime heterogeneous multi-agent systems.JournaloftheFranklinInstitute, 2013,350(3):651-669

[19]Peng C,Yang T C.Event-triggered communication andH∞control co-design for networked control systems.Automatica,2013,49(5): 1326-1332

[20]Wang X F,Lemmon M D.Event-triggering in distributed networked control systems.IEEE Transactions on Automatic Control,2011,56(3): 586-601

[21]Wang Z X,Du D J,Fei M R.Average consensus in directed networks of multi-agents with uncertain time-varying delays.Acta Automatica Sinica,2014,40(11):2602-2608

[22]Wang Z X,Fei M R,Du D J,Shang L L.Event-triggered average consensus for multiagent systems with time-varying delay.Mathematical Problems in Engineering,2014,2014:Article ID 131586

[23]Hu Y B,Lam J,Liang J L.Consensus control of multi-agent systems with missing data in actuators and Markovian communication failure.International Journal of Systems Science,2013,44(10):1867-1878

[24]Park P G,Ko J W,Jeong C.Reciprocally convex approach to stability of systems with time-varying delays.Automatica,2011,47(1):235-238

[25]Wang J F,Liu C F,Yang H Z.Stability of a class of networked control systems with Markovian characterization.Applied Mathematical Modeling,2012,36(7):3168-3175

[26]Qiu L,Luo Q,Gong F,Li S B,Xu B G.Stability and stabilization of networked control systems with random time delays and packet dropouts.Journal of the Franklin Institute,2013,350(7):1886-1907

[27]Gu K Q,Kharitonov V L,Chen J.Stability of Time-delay Systems. Boston:Birkha¨user,2003.

Zhaoxia Wang Ph.D.candidate at the School of Mechatronic Engineering and Automation,Shanghai University.She received the B.Sc.and M.Sc. degrees from Shandong University in 2002 and 2005,respectively.Her research interests include multi-agent systems and networked control systems.

She is also a lecturer at the School of Electrical Engineering and Automation,Qilu University of Technology.

Minrui Fei Professor at Shanghai University,vicechairman of Chinese Association for System Simulation,and standing director of China Instrument &Control Society.He received the B.Sc.,M.Sc. and Ph.D.degrees all from Shanghai University in 1984,1992 and 1997,respectively.His research interests include networked advanced control and system implementation,distributed and fi eldbus control systems,key technology and applications in multif i eldbus conversion and performance evaluation,as well as the application of virtual reality and digital simulation in industry.Corresponding author of this paper.

Dajun Du Associate professor at Shanghai University.He received the B.Sc.and M.Sc.degrees both from Zhengzhou University in 2002 and 2005, respectively,and the Ph.D.degree in control theory and control engineering from Shanghai University in 2010.His research interests include networked control systems,system modeling and identi fi cation.

Min Zheng Associate professor at Shanghai University.He received the Ph.D.degree in control theory and control engineering from Southeast University in 2008.His research interests include networked control systems,time delay systems,and neural networks.

t

October 10,2014;accepted April 8,2015.This work was supported by National Natural Science Foundation of China(61473182), NationalKeyScienti fi cInstrumentandEquipmentDevelopment Project(2012YQ15008703),Project of Science and Technology Commission of Shanghai Municipality(14JC1402200,15JC1401900,14ZR1414800),and Shanghai Rising-Star Program(13QA1401600).Recommended by Associate Editor Jiming Chen.

:Zhaoxia Wang,Minrui Fei,Dajun Du,Min Zheng.Decentralized event-triggered average consensus for multi-agent systems in CPSs with communication constraints.IEEE/CAA Journal of Automatica Sinica,2015, 2(3):248-257

Zhaoxia Wang is with the Shanghai Key Laboratory of Power Station Automation Technology,School of Mechatronic Engineering and Automation, Shanghai University,Shanghai 200072,China,and also with the School of Electrical Engineering and Automation,Qilu University of Technology,Jinan 250353,China(e-mail:zhaoxia6211@163.com).

Minrui Fei,Dajun Du,and Min Zheng are with the Shanghai Key Laboratoy of Power Station Automation Technology,School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,China(e-mail: mrfei@staff.shu.edu.cn;ddj@shu.edu.cn;zhengmin203@shu.edu.cn).