正交对称复合伸缩小波紧框架的构造
冯 岩, 薛 瑞,周世璇
(1.信阳师范学院 计算机与信息技术学院, 河南 信阳 464000;2.对外经济贸易大学 金融学院,北京 100029)
0 引言
小波分析是20世纪80年代中期发展起来的用于分析非平稳信号的强有力工具,是对傅立叶分析的继承、总结和发展.小波变换不仅能很好地非线性稀疏逼近一维信号,而且能高效地捕捉一维信号的点状奇异性[1-2].然而在表示高维信号时,它却不能很好地捕捉高维信号的线状奇异性[3-5].针对这一不足,众多研究人员提出了一些新的分析工具,如脊波(ridgelets)[6]、曲波(curvelets)[7]、轮廓波(contourlets)[8]、复合伸缩小波(composite dilation wavelets)[9]等等.这些变换工具的基本思想是在能最优稀疏逼近高维信号的同时,能更好地捕捉高维信号的几何特征,即它们能有效分析高维信号的局部、尺度、形状和方向信息.其中,复合伸缩小波因具有一致处理连续和离散情形的特点而受到人们青睐.
复合伸缩小波的概念是由Guo等人引入的[9-11],并发展了相关理论.与经典小波不同的是复合伸缩小波变换由两个不同的变换矩阵来实现:一个是类似经典小波中的尺度矩阵,也称为抛物矩阵;另一个是方向矩阵,它能描述不同尺度不同方向上的信息.因此,在表示高维信号时,复合伸缩小波能更准确地描述高维信号的尺度、方向和位置信息.另一方面,由复合伸缩小波构成的系统也是一种仿射系统,且具有多分辨率(MRA)的性质[9].因此,可以设计出快速分析重构算法.
在现实中存在有大量向量值数据,如彩色图像、无线多用户通讯、数字化视频等.为了更有效地处理向量值数据,Weber在文献[12]中提出了正交框架的概念.随后,Bhatt等人在文献[13]中根据酉扩充原理,由已知的正交加细函数及小波,构造出了L2(R2)中的正交小波框架,研究了向量值的离散小波变换,并把这种变换应用到彩色图像数据处理,取得了较好效果.正交小波框架在函数空间的刻画和多通道通信系统等多方面都有着重要的应用[12-14].正交小波框架的提出使得对一类向量值数据的处理更为简单[15-16],即可以用一个通道同时处理两个信号.具有对称性的小波、小波框架在图像和信息处理中具有重要作用,使用具有线性相位的滤波器可有效避免图像失真[2].
Wu等人[17]由已知的复合伸缩小波构造了对称-反对称复合伸缩多小波,Li等人[18]基于仿酉对称矩阵,由已知的紧小波框架构造出了正交对称的小波紧框架.受文献[17]和[18]的启发,本文将研究L2(Rn)空间中正交对称复合伸缩小波紧框架的构造.
1 基本知识和相关结论
本节介绍一些基本符号、概念和相关结论.R表示实数集合,Z表示整数集合,C表示复数集合.L2(Rn)表示Rn上所有平方可积函数集合.
伸缩矩阵是其特征值的绝对值大于1的矩阵,AT表示矩阵A的共轭转置,矩阵A(z)称为是仿酉对称矩阵,如果A(z)AT(z)=I.GLd(C)表示复数域上的一般线性群,即行列式不为零的d阶矩阵按照矩阵乘法构成群,SLd(C)是GLd(C)的子群,且其行列式为1.函数f∈L2(Rn)的Fourier变换定义为:
这里·表示向量的点乘.

(1)
这里‖f‖2=〈f,f〉,ψl;j,k(·)=dj/2ψl(Mj·-k),d=

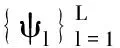
复合伸缩小波系统是一个复合伸缩仿射系统,具有多分辨率的性质,其形式为
AAB(Ψ)={DaDbTkΨ:a∈A,b∈B,k∈Zn},
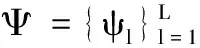
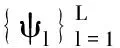
(2)
基于已知的复合伸缩小波框架和式(2)定义的对称-反对称的函数,Wu[17]等人构造了具有对称性的复合伸缩多小波框架.
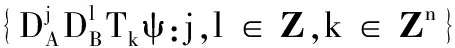
文献[9]给出了复合伸缩小波紧框架的特征.

对所有的函数f∈D,假设
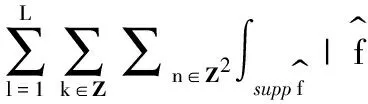


文献[14]和[12]研究了正交框架的一些性质,并讨论了它们在诸如多通道通信系统中的一些应用.下面介绍正交框架的概念和性质.

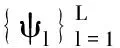
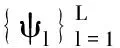
几乎处处ξ∈Rn.
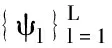
和

下面的引理给出了复合伸缩因子小波紧框架的正交性特征,它可由文献[12]中定理1.5得到.

2 具有对称正交复合伸缩小波框架的构造


证明由简单计算可得
这里,在最后一个等号中用了公式M(e-iξ)M*(e-iξ)=IQ.对几乎所有的ξ∈R2和γ∈Z2(Z2A),有
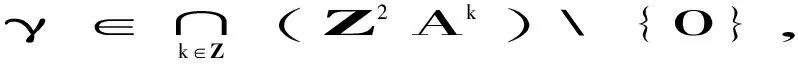
在证明过程中,用了条件M(e-iξ)×M*(e-iξ)=IQ.当γ∈Z2(Z2A)时,有

证毕.
下面的推论给出了一个由对称复合伸缩因子小波紧框架来构造对称正交复合伸缩因子小波紧框架的方法.
推论1 假设复合伸缩系统


3 例子


且令
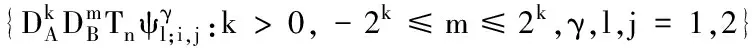
例2 根据式(2)定义
这里ψ是经典剪切波[3],c是一常数.令

4 结论
复合伸缩因子小波不仅能更好地表示高维信号的线状奇异性,而且是一仿射系统,具有多分辨率的性质.近年来,具有复合伸缩因子的小波在图像压缩、去噪、边缘分析与检测等实际中得到了广泛应用.正交小波在处理彩色图像、数字化视频、多用户通道通信系统等应用中非常方便.本文研究了具有复合伸缩因子的正交对称小波紧框架的构造方法,最后给出两个构造算例.

