考虑地震输入机制的强度折减动力有限元方法

王璨，张伯艳，李德玉

（中国水利水电科学研究院工程抗震研究中心，北京100048）

考虑地震输入机制的强度折减动力有限元方法

王璨，张伯艳，李德玉

（中国水利水电科学研究院工程抗震研究中心，北京100048）

为研究边坡在地震作用下的稳定安全性和地震波在边坡介质中的传播，基于强度折减原理，提出了能计入无限地基辐射阻尼效应的边坡地震动力显式有限元方法和与之对应的边坡失稳判定标准。编写相应的计算机程序与ANSYS/LS-DYNA计算软件实现了无缝连接。经典算例表明，本文强度折减方法和失稳判据的正确性以及AN⁃SYS/LS-DYNA无反射吸能边界的适用性，边坡工程实例分析表明上述方法在边坡动力稳定分析中具有一定的可行性。

边坡；强度折减；地震输入；失稳判据；地基辐射阻尼

1 研究背景

水利水电工程的抗震安全，在很大程度上取决于工程场址附近边坡、堆积体的抗震稳定性。虽然边坡的静力稳定分析取得了极大的进展［1］，但对边坡或堆积体的抗震稳定分析仍处于探索阶段，基于拟静力法的极限平衡方法仍是边坡抗震稳定分析最常用的方法，可是作用于边坡体上地震荷载的大小和作用方式还未达到共识，与水利水电工程边坡有关的3个现行规范［2-4］对边坡的地震作用均无条文规定，这也导致边坡抗震设计具有较大的随意性。

利用有限元分析边坡的静力稳定，使用强度折减法确定与极限平衡相类似的安全系数和滑动面［5-7］研究边坡的稳定性，日益发展成为解决边坡问题的不可或缺的技术手段，对于重要的工程边坡一般推荐使用有限元进行分析研究。在动力分析中，研究地震作用下边坡的动力反应，从而确定边坡动力失稳机理和动力稳定安全，也越来越受到人们的关注［8-10］。

地震作用下边坡稳定的有限元分析，其难点在于建立能体现无限地基效应的边坡地震输入方法以及与边坡动力失稳相对应的动力失稳判据。本文将借鉴边坡静力有限元分析中强度折减的概念，用材料非线性弹塑性模型和摩尔-库仑屈服准则模拟边坡体材料，建立边坡稳定分析的地震输入模型，使用显式有限元方法分析研究西藏雅鲁藏布江某坝址附近崩坡积体的静、动力稳定安全，并将有限元计算结果与传统的极限平衡方法进行比较，后期可为实际工程设计提供参考。

2 强度折减原理与有限元地震输入方法简介

2.1 强度折减原理土质边坡的有限元稳定分析中，常将边坡体作为非线性材料处理，应用较广泛的是Druker-Prager屈服准则的弹塑性模型，这一材料模型在大型有限元分析软件如ANSYS、MARC、PATRAN、NASTRAN中均普遍采用［7，11］。摩尔-库仑准则不仅能反映土体的抗压强度不同的S-D效应（Strength Difference Effect）及对静水压力的敏感性，且土体参数c、φ值可以通过各种不同的常规试验测定，因此与其它准则相比，更易为工程界所接受，应用更广泛［12］。虽然文献［7］推导了Druker-Prager准则与摩尔-库仑准则参数的换算关系，但直接使用摩尔-库仑准则进行计算更为方便，计算结果也更准确，因此本文采用摩尔-库仑屈服准则的弹塑性模型模拟边坡土体。

在摩尔-库仑屈服准则下进行强度折减的边坡稳定性分析，其基本原理是将边坡材料的强度参数c、φ同时除以一个折减系数Fs，得到一组新的强度参数值c′、φ′；然后以这组新的值作为输入参数进行有限元计算；通过反复试算，直至达到边坡失稳的临界状态，此时对应的折减系数Fs即为边坡的最小安全系数。对c、φ值的具体折减公式如下：

其中：

对于静力分析而言，判断边坡模型失稳的临界状态主要有以下判别标准［7］：（1）以有限元数值计算迭代过程不收敛作为判别标准；（2）以等效塑性应变从坡脚到坡顶贯穿作为判别标准；（3）以滑动土体无限移动作为判别标准，此时土体滑动面上特征点的应变和位移发生突变且无限发展。

等效塑性应变是用来确定材料经强化后屈服面位置的物理量，用塑性应变增量的简单组合来确定，其定义式如下：

利用有限元强度折减方法，使边坡处于临界破坏状态时，临界滑面上的点往往是沿深部方向的等效塑性应变最大的地方，因此可以根据临界平衡状态的等效塑性应变分布来大致估计临界滑面。与极限平衡方法相比，强度折减法不需事先假定滑动面的形状就可直接求得边坡的安全系数，并可由变形图表示出滑面的大致位置，具有一定的优越性。

边坡动力失衡的准则可参照上述静力分析的边坡失稳判别准则而定，但地震具有往复振动的特征，且模型整体非线性使得很难预估边坡的破坏形态，本文将以位移、等效塑性应变等动力响应，综合判断边坡是否失稳。

2.2 地震输入方法在极限平衡分析中，地震被简化为大小与方向均不变的荷载，这与实际的地震作用相差较大。事实上，地震是地震波在介质中的传播过程，大小与方向均随时间变化。另外，由半无限地基中截取有限范围的计算模型，在模型边界上将产生波的反射效应［13］，一般来说，可以通过施加黏弹性边界或黏性边界来消除波的反射效应［14］，本文将利用LS-DYNA无反射吸能边界来实现这一目标。该吸能边界可以防止在人工边界产生的应力波反射重新进入模型。

根据地震工程学相关理论［15］，可以认为近场地震波接近由基底垂直向上入射，而从远处向上垂直入射的地震波在均质半无限空间上具有理论解，由此可获得自由场速度和自由场应力。

图1是利用ANSYS/LS-DYNA程序分析边坡动力稳定时，如何输入地震作用的示意图，图中有限元域划分有限元网格，在有限元边界上将地震波动产生的自由场速度向量和自由场应力张量转化为相应的节点力矢量。其效果是将地震波动问题转化为内源问题，而LS-DYNA的无反射边界条件，不会在边界产生波的反射。

图1 边坡地震作用输入

式中：Ab为有限元边界节点的影响面积；n为边界外法线方向余弦向量；Cb为3×3的对角矩阵，其分量大小视为纵波或剪切波而有所不同，对于纵波，cbp=ρcpAb，对于剪切波，cbs=ρcsAb，cp、cs是P波和S波波速。

其中，P为施加的静外力向量（包括体力经转化的等效结点力）；FB为作用于边界的地震力向量，是式（4）求得的Fb在全部边界上的矢量和；Fint为内力向量，它由下面几项构成：

采用中心差分时间积分的显式方法，计算体系各节点在第n时间步结束时刻的加速度向量：

式（6）中3项依次为当前时刻单元应力场等效节点力（相当于动力平衡方程的刚度项）、沙漏阻力和接触力向量。

节点速度和位移向量通过下面两式计算：

新的几何构型由初始构型x0加上位移增量获得，即：

从计算效率的角度来讲，显式动力分析的优点有二：其一为不形成总体刚度矩阵，弹性项放在内力中，避免了矩阵求逆；其二为质量阵是对角阵，利用上述递推公式求解运动方程时，仅需利用矩阵乘法即可获取右端的等效荷载向量。需要指出的是，质量矩阵的对角化常常还能显示出精度的改善［16］，本文没有比较不同形式的质量矩阵对计算精度的影响，采用通用程序LS-DYNA显式分析，应能满足计算精度的要求。通过编写相应的程序，式（5）的地震力可以作为右端力项通过LS-DYNA显式分析求解，从而实现边坡稳定分析的地震输入。

时间步与时间点的定义为：

3 模型验语

为验证上述强度折减原理和地震输入中吸能边界的效果，本文选用两个算例进行计算验证。其一为一个二维均质土坡，利用强度折减原理计算其稳定安全系数。坡面几何形状如图2所示，坡高10 m，坡角26.56°，材料参数为：凝集力，摩擦角φ=19.6°，比重，弹性模量E=10 MPa，泊松比μ=0.25。在自重作用下，通过选用不同的折减系数，用LS-DYNA程序计算边坡的静力反应。图2为折减系数为1时算例边坡的等效塑性应变，从坡脚到坡顶基本贯穿。若以等效塑性应变从坡脚到坡顶贯穿作为边坡失稳的判别标准，则得到算例边坡的静力稳定安全系数约为1.0，与极限平衡方法所得安全系数一致。

图2 折减系数为1时等效塑性应变

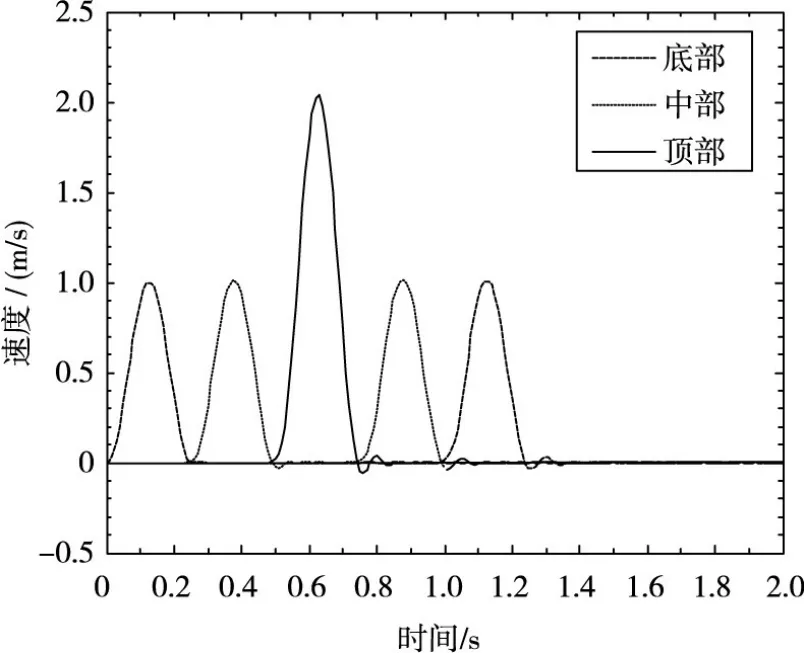
图3 底部、中部、顶部速度时程

其二为一半平面空间体，材料弹性模量E为24 MP，剪切模量G为10 MP，泊松比μ为0.2，质量密度为1 000 kg/m3，阻尼比为0，在其底部作用垂直向上入射的水平向单位脉冲速度波（见u̇0() t=，可获得理论解。将这一半无限平面问题，离散为有限模型，其长、高各为26 m和50 m，应用上述地震输入方法，进行显式有限元分析，得到底部、中部和顶部的速度响应，如图3所示。从图3可见，有限元计算结果与理论解一致，表明上述边坡地震输入过程中吸能边界很好的吸收了外传波，具有和黏弹性边界或黏性边界相当的吸能效果，且使用简单方便。

4 工程应用

4.1 工程概况及计算参数位于西藏自治区山南地区的某水电站，为二等大（2）型工程，坝址区主要物理地质现象表现为岩体风化、蚀变、卸荷、泥石流及崩坡积体。其中C1崩坡积体对大坝安全的影响很大，是值得高度关注的崩坡积体。为保障工程的顺利施工和长期运营，应对C1崩坡积体稳定安全进行深入分析和研究。C1崩坡积体前后缘高差约390 m，纵坡向长约560 m，横向宽度66～330 m，分布面积约10.5万m2，厚度约10～72 m，水平向最深可达120 m，总体积约180万m3。由3种材料构成，包括块石、碎石和混合土，材料特性见表1。

表1 材料特性

C1崩坡积体简化为平面问题，其1-1剖面是最不利剖面。对1-1剖面进行有限元网格剖分，共有节点11 868，单元7 624个，自由度23 736，有限元网格剖分见图4。C1崩坡积体按A类II级边坡设计，静、动力设计安全系数依次为1.15和1.05，C1崩坡积体抗震设计标准与主要水工建筑物相同，采用50年超越概率10%的基岩水平向地震动峰值加速度1.76 m/s2设计，边坡设计反应谱为水工抗震规范中重力坝的标准设计反应谱，其特征周期取0.2 s，反应谱最大值的代表值为2.0，阻尼比取10%，按此反应谱生成了水平向和竖向30s的人工合成地震波，竖向峰值加速度为水平向的2/3，地震动时程见图5。

图5 加速度时程

4.2 计算分析静力分析时，拟定强度折减系数依次为1.0、1.1、1.2和1.3，通过对各计算工况的等效塑性等值线图的观察可知，当强度折减系数为1.3时，等效塑性应变从坡脚到坡顶基本贯穿，且在坡顶处，个别单元等效塑性应变极大（见图6），所以可以认为天然状态下静力安全系数约为1.30。采用中国水利水电科学研究院陈祖煜院士开发的STAB边坡稳定分析程序，用Morgenstern-Price法进行极限平衡分析，得到静力安全系数为1.29，与强度折减法得到的安全系数较接近。

图6 强度折减系数1.3时地震前塑性区

图7 强度折减系数1.15时地震后塑性区

图8 强度折减系数1.15时Y向位移等值线图

有限元动力计算是在完成相应静力分析的基础上，对图5所示的水平向和竖向设计地震动作用下进行的。本文依次完成了强度折减系数1.0、1.05、1.1、1.15和1.16时，设计地震作用下的C1崩坡积体的动力显式有限元分析。观察地震作用过程中，等效塑性应变随时间的变化，可以发现，在地震作用下，等效塑性应变会不断增加。但与静力分析不同，无“从坡脚到坡顶贯穿”的现象，因此，无明确的滑动面。当强度折减系数为1.15时，从边坡中部表面区域至坡脚处有“明显的滑移区”（见图7）。通过时间历程的位移等值线动画图（见图8）可以看出，边坡的初始破坏发生在坡顶，随着时间的增加，破坏逐渐向边坡的中部高程和坡脚地表处移动，且强度折减系数大于1.16时，有限元计算不收敛，所以可以认为动力强度折减安全系数约为1.15。

5 结语

本文采用考虑地震输入机制的强度折减动力有限元方法，进行了算例验证和实际边坡工程计算分析，研究结果表明，通过编写相应的计算机程序与ANSYS/LS-DYNA计算软件可无缝连接，模拟边坡理想弹塑性材料的摩尔-库仑屈服特性，进行有限元强度折减，采用“明显出现滑移区，动力计算不收敛”等综合判断方法，可合理确定边坡动力稳定安全系数。另外，本文采用的地震动输入方法，在有限元人工边界上将地震波动产生的自由场速度向量和应力张量转化为相应的节点力矢量进行加载，将地震波动问题转化为内源问题，可准确模拟地震作用下无限地基效应，为边坡抗震稳定分析提供了可供选用的方法。

［1］陈祖煜.土质边坡稳定分析－原理·方法·程序［M］.北京：中国水利水电出版社，2003.

［2］SL 386—2007，水利水电工程边坡设计规范［S］.北京：中国水利水电出版社，2007.

［3］DL/T 5353—2006，水电水利工程边坡设计规范［S］.北京：中国电力出版社，2007.

［4］DL 5073—2000，水工建筑物抗震设计规范［S］.北京：中国电力出版社，2001.

［5］Griffiths D V，Lane P A.Slope stability analysis by finite elements［J］.Geotechnique，1999，49（3）：387-403.

［6］Matsui T，San K C.Finite element slope stability analysis by shear strength reduction technique［J］.Soils and Foundations，1992，32（1）：59－70.

［7］郑颖人，赵尚毅，宋雅坤.有限元强度折减法研究进展［J］.后勤工程学院学报，2005（3）：1-6.

［8］Jibson R W.Methods for assessing the stability of slopes during earthquakes-A retrospective［J］.Engineering Geology，2011，122：43-50.

［9］Zhao T，Sun J，Zhang B，et al.Analysis of slope stability with dynamic overloading from earthquake［J］.Journal of Earth Science，2012，23：285-296.

［10］郭院成，陈涛，钱辉.基于强度折减的边坡动力安全系数确定方法研究［J］.土木工程学报，2012，45（2）：117-120.

［11］李颢，张风安，姚环.Ansys强度折减法在开挖边坡稳定分析中的应用［J］.电力勘测设计，2008（4）：10-13.

［12］刘英，于立宏.Mohr-Coulomb屈服准则在岩土工程中的应用［J］.世界地质，2010，29（4）：633-639.

［13］杨正权，刘小生，汪小刚，等.土石坝地震动输入机制研究综述［J］.中国水利水电科学研究学院学报，2013，11（1）：27-33.

［14］刘云贺，张伯艳，陈厚群.拱坝输入模型中黏弹性边界与黏性边界的比较［J］.水利学报，2006，37（6）：758-763.

［15］胡聿贤.地震工程学［M］.第二版，北京：地震出版社，2006.

［16］Zienkiewicz O C.有限元法（下册）［M］.北京：科学出版社，1985.

A strength reduction dynamic FEM including the seismic input mechanism

WANG Can，ZHANG Boyan，LI Deyu
（Earthquake Engineering Research Center，IWHR，Beijing100048，China）

In order to study the safety of slope stability during earthquakes and seismic wave propagation in slope media，on the basis of strength reduction theory，this paper introduces a slope seismic dynamic ex⁃plicit finite element method including unlimited foundation radiation damping effect and proposes some corre⁃sponding slope instability criteria.This paper also develops the related coding computer programs that seam⁃lessly match the corresponding ANSYS/LS-DYNA software.Moreover，some classical calculating examples show the correctness of strength reduction theory and instability criterion and display the utility of the nonre⁃flecting boundaries used in ANSYS/LS-DYNA.In addition，with some examples of actual slope engineering analyzing，the results that show the proposed method is feasible in slope stability analysis.This paper pro⁃vides an available method for future studies of slope stability during earthquakes.

slope；strength reduction；ground motion input；instability criterion；foundation radiation damp⁃ing

TV313

A

10.13244/j.cnki.jiwhr.2015.02.003

1672-3031（2015）02-0100-06

（责任编辑：王冰伟）

2014-10-08

水利部公益性行业科研专项资助项目（201001035）

王璨（1990-），女，河南南阳人，硕士生，主要从事工程结构抗震研究。E-mail：13381111269@163.com