一种最大共轭梯度连续泛函的网络峰值预测

陈卫军，金显华

(安阳师范学院 软件学院，河南 安阳 455000)

0 引言

随着网络的迅速发展，网络上承载的业务和应用日益丰富.因此加强网络管理是运营商们急需解决的问题.有效地提高网络运行速度和利用率，网络峰值起到决定性作用.网络峰值预测是业务管理的关键问题，网络峰值的精确性、实时性和广谱性直接关系到业务管理的效率和性能.网络峰值预测就是对尚未发生和目前还不明确的网络信息，根据过去和现在的网络信息进行预先的估计和推测，即在一定的算法模型下对未来一段时间内的网络峰值信息的发展趋势、方向和可能的状态做出合理的、在允许误差范围内的推断.网络峰值的预测涉及网络流量、网络信号强度和网路峰值范围等多种因素，因此研究网络峰值预测算法，具有重大的理论和实践意义，而相关模型的构建和算法研究受到人们的关注[1].

对网络峰值走势的预测模型构建，根本上是对一组影响网络峰值的样本数据的处理，这个处理过程是对这个样本序列进行估计预报的过程.传统方法中，主要采用线性模型或者等效近似的线性模型对网络峰值影响的样本序列进行处理和分析，并取得了一定的研究成果.文献[2]提出一种基于改进灰色神经网络的网络峰值走势分析模型,但算法仅仅考虑样本序列的线性成分，对灰色关联的非线性成分的处理没有纳入分析范畴，导致预测精度不高.文献[3]构建了一种网络流量、网络信号强度和网络峰值的关联模型,对网络峰值预测精度较好，但是算法模型需要从长期均衡角度上看网络流量对网络峰值的影响，实践中操作困难.文献[4]提出一种基于贝叶斯估计的动态随机一般均衡模型，实现对网络峰值与网络管理者的调控模型，但算法不能够准确地拟合诸多非线性动力模型影响下的网络峰值预测，导致对网络峰值预测精度不好，且算法开销较大.

针对上述问题，提出一种采用最大共轭梯度连续泛函的网络峰值预测算法.算法首先建立简单的SVM模型，在SVM模型的基础上，采用PCA方法实现对原始网络峰值波动序列的加权平滑处理，采用最大共轭梯度连续泛函的样本序列数学处理方法实现预测算法的改进.仿真实验验证了网络峰值预测算法的有效性.

1 网络峰值预测原理

1.1 网络峰值预测影响因素与模型设计

首先需要进行统计模型的构建，在网络峰值预测算法设计中，需要建立一个包含网络流量、网络信号强度和网络峰值的SVM模型，采用SVM模型的主成分分析方法实现对网络峰值的PCA估计系统设计[5].网络峰值估计和预测的SVM模型是基于数据的统计性质建立的模型，选取我国2006年3月到2013年10月的网络峰值月度数据作为原始数据样本序列，样本序列数学表达式为

U={U1,U2,U3,…,UN}，

(1)

其中Ui为维数为d维的随机变量，各个随机变量Ui之间是相互独立的.峰值影响的参量模型中，峰值增长率选取1～3年短期增长率数据[6-8]，增长率序列的概率密度函数为：

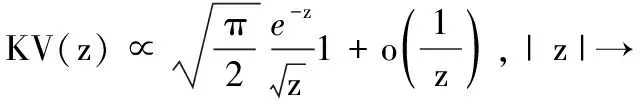
(2)

(3)

在建模前，对各变量数据进行自然对数变换，峰值波动数据X符合稳定分布特征，记为X～sα(σ,β,μ)，β的最大似然估计可通过求各数列的单位根检验和协整检验得到.当V为连续变量，则特征函数满足：

Φ(ω)=E[ejωX]=

(4)

式(4)表示一个包含网络流量、网络信号强度和网络峰值3个内生变量的网络峰值波动模型，其模型的数学表达式为

(5)

式(5)中，n=1,2,…,N；υi(x)为一个k维内生变量.在网络峰值关联参数估计中，增长率为m取得一维数组Xn，它表示约束算法下最大化消耗指数，与之最相关的网络流失率为Xη(n)，从而构建得到能影响网络峰值关联预测影响因素的均衡方程：

(6)

式(6)中，通过最大共轭梯度连续泛函，在奇异半正定性双周期性复分析下，得到迭代对数似然函数sgn(ω)的期望值，由此实现对网络峰值关联预测.峰值影响的参数取值面积示意图如图1所示.

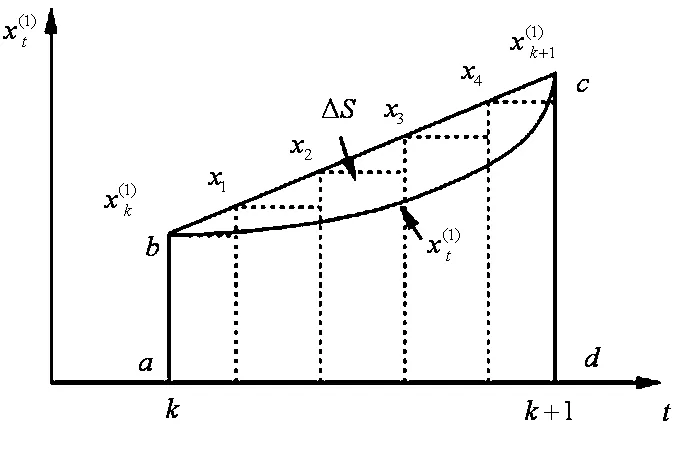
图1 网络峰值影响的参数取值面积示意图

1.2 网络峰值预测模型原始数据预处理

对网络峰值的研究，首先是把峰值样本序列当作一个时间序列，采用信号处理学科的理论进行.因此，要对网络峰值使用信号处理方法进行原始数据的预处理.

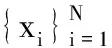
dm(0)=‖Xm-Xk‖.

(7)

式(7)中，Xm和Xk通过一步发展演变为Xm+1和Xk+1，由此为实现峰值的准确预测提供数据基础.采用最大共轭梯度连续泛函方法，得到n+m+k(k>0)时刻数据的预测值，它表示为两向量增长变化分类的指数：

‖Xm+1-Xk+1‖=‖Xm-Xk‖eλ1.

(8)

式(8)中，Xm+1的最末分量x(tn+1)未知，且唯有它是未知的.其计算式表达为：

Xm+1(m)=Xk+1(m)±

(9)

式(9)中:dm(0)表示脉冲响应函数分别分析利率，Xm+1(i)表示网络流量对网络峰值的影响贡献程度，Xk+1(i)表示样本个数.由此建立了简单的SVM模型，在SVM模型的基础上，结合最大共轭梯度连续泛函，实现对原始峰值波动序列的加权平滑处理与准确预测.

2 基于一种最大共轭梯度连续泛函的网络峰值预测模型

2.1 最大共轭梯度连续泛函的提出与峰值波动序列平滑处理

首先对初始条件不同的网络峰值进行在线评估，峰值波动曲线在运动发展的过程中,随着时间的进程呈现指数分离.考虑网络流量和网络信号强度对网络峰值的贡献，采用辅助矩阵的方法，进行最大共轭梯度连续泛函，最大共轭梯度为：

(10)

在考虑峰值因素和网络流失的情况下，采取一次性总付的形式增加的峰值预算约束化成本，引入网络峰值指数的同比增长率，得到新的状态项为

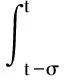
(11)

最大共轭梯度连续泛函下的峰值序列的主成分分析结构状态项和积分叉积项分别表示为：

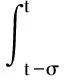
(12)

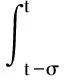
(13)

由于网络信号强度和网络峰值互为影响，因此可以对数据的统计模型进行连续泛函求导，得到峰值关联预测的目标函数为：

FY(χ;α,λ)=1-

(14)

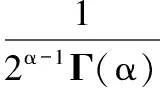
2.2 最大共轭梯度连续泛函算法的实现

根据上述分析，得到本文提出的最大共轭梯度连续泛函的网络峰值预测算法实现的关键步骤描述如下.

(1)分别对网络峰值对数hj-1(t)的局部极大值和极小值点进行插值拟合，对数据的处理以及模型估计采用方差分解的方法，对网络峰值进行SVM拟合，计算包络线的均值曲线mj-1(t).

(2)考察增长率波动以及网络流量对网络峰值的影响贡献程度，从hj-1(t)中去掉均值曲线得到hj(t)，即：

hj(t)=hj-1(t)-mj-1(t).

(15)

(3)考察hj-1(t)和hj(t)是否满足网络峰值对数和增长率的突发性变化和尺度特性筛选终止条件，即：

(16)

当满足上述条件，依据协整检验结果，可以得到协整方程，并利用支持向量机SVM模型对网络峰值波动的关联特征进行预测：

ri(t)=ti-1(t)-ci(t).

(17)

(4)若i=i+1的极值点不少于两个，则i=i+1，并转到(3)，否则分解完成，ri(t)为残余量.得到预测后的协整向量为：

(18)

(5)估计AR特征多项式的特征系数，对峰值关联特征进行状态信息融合处理，减少预测误差，得到预测结果为：

(19)

(20)

(6)令t=t+1，跳转到步骤(1)，重复计算下一时刻样本数据，直至结束.

(7)算法结束.

3 实验结果与分析

为了测试本文算法对网络峰值预测模型的性能，需要进行仿真实验,分析工具为Matlab,对网络峰值对数、网络流量对数等参数进行分析比对.上述参数分别表示为：

表1 网络峰值的协整向量估计表(104T)

在网络峰值影响因素中，网络流量具有持续性，网络信号强度起到关键作用，影响较大[9].根据上述参数设计和算法处理分析，得到原始峰值数据的样本波形图如图2所示.

以此为研究对象，对数据序列进行最大共轭梯度连续泛函预处理和平滑处理，然后采用本文算法和传统方法进行峰值关联预测，得到预测结果如图3所示.图3中给出了本文算法模型下对网络峰值预测结果和预测误差.

分析图3中的结果可见，采用本文算法，预测精度较高，预测误差控制在1.5%以内.采用传统方法对网络峰值进行预测，误差较大，对网络峰值的宏观调控指导意义受限.本文方法使得预测误差得到有效控制，且能实现对各种影响因素的关联性分析，实现关联预测.

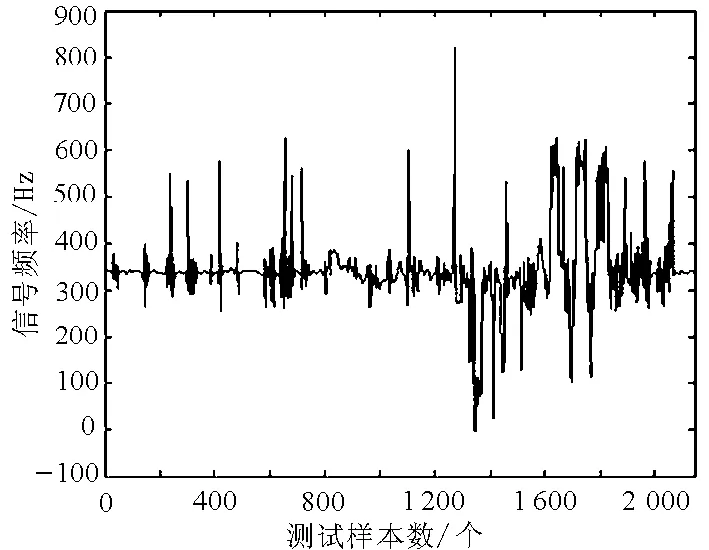
图2 原始的网络峰值数据的样本波形图

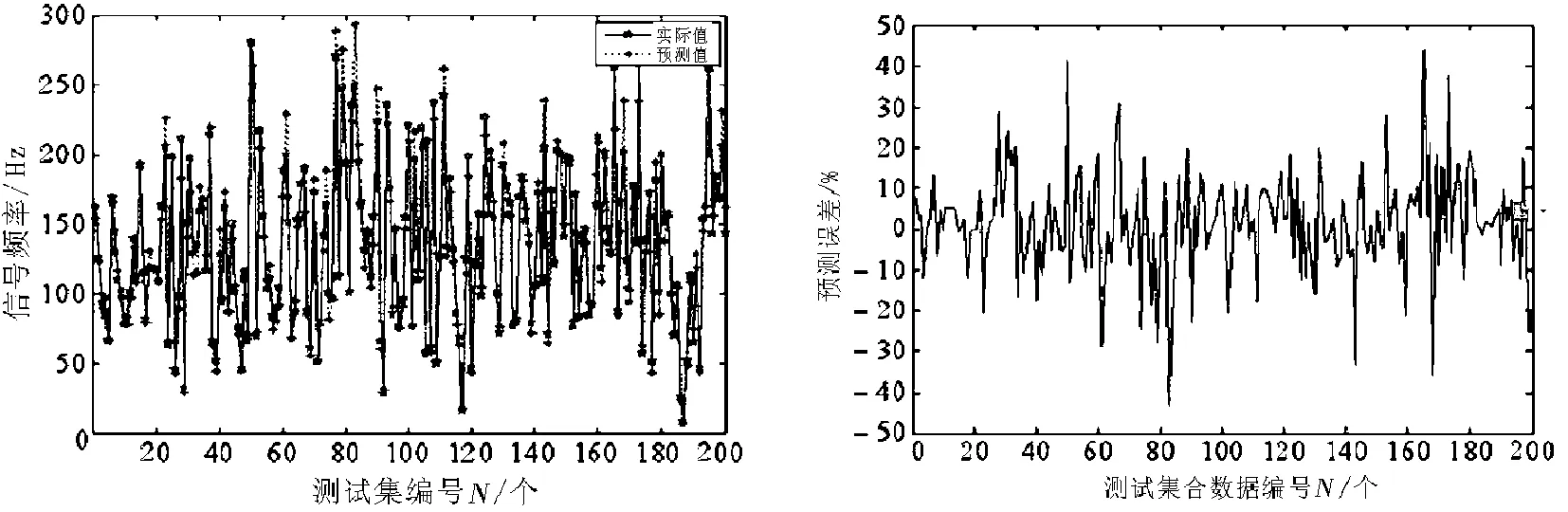
(a) 预测值 (b) 预测误差分析

4 结论

随着网络的迅速发展，网络上承载的业务和应用日益丰富.传统的方法对网络峰值进行预测只是单一采用线性或者非线性的方法进行处理，这种片面性造成预测的准确度和实时性难以保证.本文提出一种采用最大共轭梯度连续泛函的网络峰值预测算法，实现对原始峰值波动序列的加权平滑处理，采用最大共轭梯度连续泛函的样本序列数学处理方法，实现预测算法的改进.实验结果显示，本文的预测模型和算法设计，预测精度较高，预测误差控制在1.5%以内，且能实现对各种影响因素的关联性分析，性能优越，可以有效提高网络运行速度和利用率.