一类比例依赖的捕食系统局部能控性及最优控制

向会立，王 刚

(1.湖北民族学院 数学系，湖北 恩施 445000；2.河南城建学院 数理学院，河南 平顶山 467036)

0 引言

为了刻画生物种群及其之间相互作用的各种动力学行为，学者们建立了各种各样的数学模型[1-8].过去几十年来，动力学模型的渐近行为始终是生态学家们普遍关注的问题，与此相关的结果也比较丰富[2-3,5,7].近年来，关于生态模型的控制问题[4]，越来越受到研究者们的关注，尤其是有限时间内的最优控制问题.本文基于如下一类比例依赖的捕食模型[2]：

(1)

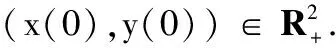
由于食饵种群的增长率在一定程度上依赖于食物源，这里不妨将食饵投放量作为控制输入.为此将方程(1)中的a用a+u来替换,从而得到如下控制系统：

(2)

下面将着重讨论系统(2)正平衡态的局部能控性、在给定的优化性能指标泛函下最优控制的存在性及最优控制的具体形式.

1 系统正平衡态的局部能控性

下面研究系统(2)正平衡态的局部能控性，并给出其局部能控的充分条件.

由文献[2]，有如下结论：

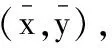
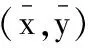
证明记

则系统(2)可以简化为：

(3)

(4)

式(4)可写为

(5)

其中

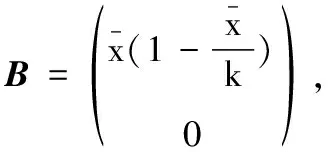
进而有

rank(BAB)=

显然，由条件f>d及cd>f(c-ma),易得

rank(BAB)=2,

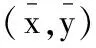
例1 在系统(2)中取a=0.02，k=50，c=0.03，d=0.01，f=0.05，m=2，得到如下系统：

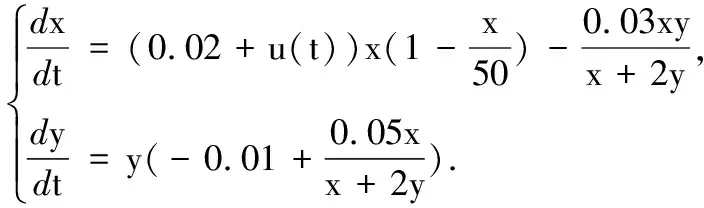
(6)

直接计算得

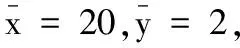
cd=0.000 3，f(c-ma)=-0.000 5，

显然满足定理1的条件.现将上述系统在平衡点(20,2)及u(t)=0处线性化得：

从而由Kalman 秩条件易知系统(6)在平衡点(20,2)局部能控.

2 系统最优控制的存在性及最优控制

本节主要讨论系统(2)的最优控制问题，根据现实情形，给定容许控制集

Φ={u∈L1[0,T],0≤u(t)≤b}.

(7)

我们的主要目的是最大化捕食者和食饵种群的密度，同时最小化食饵投放量，为此设定如下性能指标泛

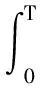
(8)

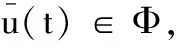
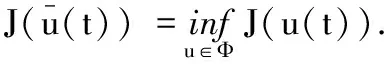
(9)

引理2[2]系统(2)的非负解(x(t),y(t))在[0,T]上一致有界.

基于上述结论，给出本文的第二个主要结论如下：

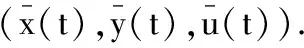
证明因为x(t)，y(t)，u(t)均有下界，故

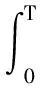
有下界，从而必有下确界，不妨记其为

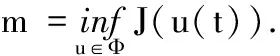
(10)

由下确界的定义，必存在一个最小化序列(xn,yn,un)使得对于任意的n∈N+有

(11)

而且序列(xn,yn,un)同时满足方程

(12)

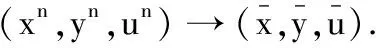
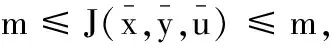
即

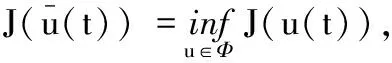
且同时成立

从而定理2得证.证毕.

下面我们给出本文的第三个主要结论：

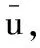
(13)

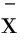
终值条件为:

λ1(T)=0,λ2(T)=0.

证明构造哈密尔顿泛函如下

H(x,y,u,t)=u(t)-x(t)-y(t)+

由庞德里亚金最小值原理有

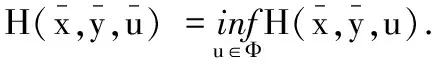
注意到

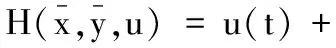
3 结论

将食饵投放量作为系统的控制量，讨论了一类具有比例依赖的食饵-捕食系统的局部能控性及最优控制问题.利用Kalman秩条件，得到了系统正平衡态局部能控性的充分条件，并证明了相应的最优控制为Bang-Bang 控制.结果表明系统在平衡态附近能够较好地控制和调节，而且开关形式的最优控制具有较强的可操作性.