单机上考虑运输的退化工件的在线排序问题

刘其佳, 冯 琪

(1.郑州大学 数学与统计学院, 河南 郑州 450001； 2.中原工学院 理学院, 河南 郑州 450007)

0 引言

在经典排序问题中，一般将工件的加工时间视为常数.而在实际问题中，工件的加工时间会随着机器老化等问题而增加.文献[1]首次提出了具有退化效应工件的排序问题.文献[2]对工件的加工时间是开工时间的简单线性函数的单机问题进行了讨论.而文献[3]是在具有退化效应的基础上考虑了工件的可拒绝性,给出了两种模型，分别是目标函数为最大时间表长加上误工工件的惩罚费用和加权完工时间、加上误工工件的惩罚费用.对于这两个问题，文献[3]均给出了NP-hard证明，并分别给出了拟多项式算法和一个FPTAS.但在实际问题中，一个决策者并不一定在一个决策时刻知道所有工件的所有信息.因此近些年在线排序也被越来越多的人研究.文献[4]对三类在线模型，其目标函数分别为最大时间表长、完工时间及最大运输完工时间的排序问题加以研究，均给出了最优的在线算法.

另外这些年考虑工件运输的在线排序问题也得到深入的研究.文献[5]考虑单机上的在线排序问题，其中每个工件都有一个运输时间，而且运输工具充分多.在这个模型下，他们给出了最好可能的在线算法.文献[6]研究了单机上运输有限制的在线排序问题，给出了问题的下界和一个在线算法.文献[7]研究了单台平行批处理机上的在线排序问题，每个工件有各自的运输时间且运输车辆充分多，并且工件的加工时间均限制在一个区间内.对这个问题，文献[7]给出了最好可能的在线算法.文献[8]则研究了单台机器上只有一台运输车辆的在线排序问题，对于不同的情形，分别给出了在线算法.

对于一个在线排序问题，通常是先找到问题的下界，即通过设计一个实例，使得任意一个在线算法应用到该实例上得到的目标值与离线最优值的比尽可能地大.决策者在设计在线算法时，算法的竞争比越接近于问题的下界，算法的性能越好.当在线算法的竞争比与问题的下界相吻合时，该在线算法就是最好可能的在线算法,这也意味着该在线排序问题被彻底解决.本文研究了单台机器上工件具有退化效应且只有一台运输车辆的在线排序问题，给出了该问题的一个下界，并给出了达到下界的最好可能的在线算法.

1 排序问题的描述

设有n个工件J1,…,Jn按时间在线到达.只有当工件Ji到达后，才能知道它的加工时间pi、退化率ai及到达时间ri.设工件的加工时间依赖于工件的开工时间，即pi=ait，其中ai≥0，1≤i≤n.由于工件的加工时间和其开工时间有关，一般假定所有的工件均在t0时刻及之后到达的.工件先在机器上加工，然后完工的工件再由运输车辆将其运送给某个顾客.目标是最小化最大运输完工时间.记T是机器和顾客之间一个来回所花费的时间.由于事先不知道要送给哪个顾客，所以假定当第一个工件到达时立刻知道顾客的位置，进而确定T的大小.每个工件Ji的运输完工时间用Di表示，指车辆将工件运送给顾客并返回到机器的时刻.所研究的问题用三参数表示法表示为

1→D|online,rj≥t0,pj=ajt,v=1,c=∞|Dmax,

令Bi是一个运输批，下面给出将要用到一些记号：

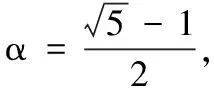
•U(t):时刻t已经到达还未加工的工件集合；

•A(t):时刻t已经在机器上完工并等待运输的工件集合；

•ρ(Bi):运输批Bi的准备时间，即Bi工件的最大完工时间；

•δ(Bi):车辆开始运送Bi的时刻，显然在任意一个可行排序中有δ(Bi)≥ρ(Bi);

•D(Bi)=δ(Bi)+T，指运输批Bi的运输完工时间.

2 排序问题的下界

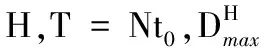
α(t0+T)+t0+T,

而最优排序是在t0时刻加工工件J1并在完工时立刻运输，进而有

因此

接下来，考虑t*<α(t0+T)的情形.假定算法H是在时刻s开始运送工件J1.如果s≥α(t0+T)，则不再有新工件到达.这时

而在最优排序中依然是在t0时刻加工工件J1并在完工时立刻运输，进而有

因此，当N→+∞时，有

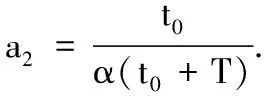
最优排序中先在t0时刻加工工件J1,然后在s+ε时刻加工工件J2，最后将这两个工件一起运送，因此有

进而，当ε→0,N→+∞时，

由上面工件实例的分析可得到引理1.

引理1 排序问题

1→D|online,rj≥t0,pj=ajt,v=1,c=∞|Dmax

的下界为1+α.

3 在线算法及竞争比分析

在本节中将给出排序问题

1→D|online,rj≥t0,pj=ajt,v=1,c=∞|Dmax的一个最好可能的在线算法.首先给出排序问题的在线算法：

算法D

加工阶段：在时刻t，如果机器是空闲的且U(t)≠∅，则从U(t)中选出工件Jj，其中工件Jj满足aj=min{ai:Ji∈U(t)}，并在时刻t在机器上加工工件Jj.否则，只需等待.

表1为某城市轨道交通列车运营日计划表。早高峰车次为0202、0402、0702、1002，晚高峰车次为1702、1802、1902、2002；每个车次都有其发车方向， 0102、0302、0402、0602、0902、1102为上行方向，其余车次为下行方向。

运输阶段：在时刻t且A(t)≠∅时，将A(t)中的工件看作一个运输批.如果机器是空闲的，t≥αT，且U(t)=∅，则在时刻t立即运输批A(t).否则，只需等待.

事实上，算法D的加工阶段执行的算法是一个贪婪算法，而一个贪婪算法是说只要有已经到达的可用工件，算法可以以任意一个顺序将其安排在机器上加工.而对于算法的运输阶段，机器是空闲的就说明此时没有工件正在机器上加工.而U(t)=∅说明此刻没有已经到达且未加工的工件.而这两个条件说明只有在没有正在加工的工件同时没有已经到达且未加工的工件时，车辆才有可能开始运送一个运输批.

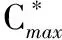
引理2[4]对于排序问题1|rj≥t0,pj=ajt|Cmax贪婪算法可以得到最优的排序.

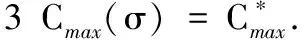
证明由算法D的加工阶段执行的算法是一个贪婪算法，再由引理2可知，排序σ是排序问题

1|rj≥t0,pj=ajt|Cmax

在本文讨论的排序模型中，运输车辆的容量是充分大的，由此可以得到以下的引理.

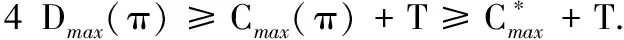
下面由以上这些引理来分析算法的竞争比.

定理1 算法D的竞争比为1+α，即

Dmax(σ)/Dmax(π)≤1+α.

证明令B1,…,Bk是排序σ中按此顺序运输的运输批.令nB=|{B1,…,Bk}|.并假定rl是工件的最晚到达时刻.由算法D运输阶段的算法，对于1≤i≤k，有δ(Bi)≥αT.如果δ(Bk)=αT，那么nB=1.进而

Dmax(σ)=δ(Bk)+T≤(1+α)Dmax(π),

从而此情形得证.接下来假定δ(Bk)>αT.分两种情形来讨论：

情形1δ(Bk)=Cmax(σ)，则有

从而此情形得证.

情形2δ(Bk)≠Cmax(σ).这说明运输批Bk是紧跟在运输批Bk-1之后运输的，因而有

δ(Bk)=δ(Bk-1)+T,

进而得到

Dmax(σ)=δ(Bk-1)+2T.

(1)

由于运输车辆的容量充分大，由算法D的执行可知，rl>δ(Bk-1).注意到对于1≤i≤k，有δ(Bi)≥αT，从而得到

Dmax(π)≥rl+T>δ(Bk-1)+T≥αT+T,

即T≤αDmax(π).

式(1)可以重新写为

Dmax(σ)=δ(Bk-1)+2T

从而定理得证.证毕.

由引理1及定理1可得以下结论.

定理2 对于排序问题

1→D|online,rj≥t0,pj=ajt,v=1,c=∞|Dmax，

在线算法D是最好可能的，且竞争比为1+α.

4 结论

本文所考虑的工件实际加工时间与工件的开始加工时间有关，目标函数是与实际生产环境对应的，考虑了单机上工件具有退化性并考虑工件运输的在线排序问题，给出了该问题的下界1+α，并给出了达到下界的最好可能的在线算法D.在今后的研究中，可以考虑车辆容量有限制的情形及其他更为复杂的目标函数.