出行分布观测数据中的稀疏矩阵问题研究

罗小强

（长安大学建筑学院，西安710064）

出行分布观测数据中的稀疏矩阵问题研究

罗小强*

（长安大学建筑学院，西安710064）

对出行分布观测数据中的稀疏矩阵问题进行分析，提出了部分矩阵估计、补零矩阵估计和增量矩阵估计3种不同方法来标定双约束重力模型的参数.通过定义估计的精确性和有效性两个不同的估计效果测度，将双约束重力模型等价为带有约束的数学规划，并采用解析方法比较3种不同标定方法的估计精度差异.在此基础上，通过数值方法模拟计算，并比较3种标定方法的估计有效性.通过研究可以发现，补零矩阵估计的参数精确性最好，而增量矩阵估计的有效性最好.研究成果能够作为实际城市交通规划中观测稀疏矩阵参数标定工作的理论依据.

城市交通；稀疏矩阵；参数标定；重力模型；误差估计

1 引言

在城市交通规划实践中，通过实际调查所得到的出行矩阵往往含有很多零元.假如某城市共划分了100个交通小区，每个交通小区平均2万人左右.若为分析需要而划分了9种出行目的、5个出行时段及7种交通方式，那么在分目的分时段分方式的出行矩阵分析中要使每个点对之间至少有一次出行被观测到，观测出行量至少为315万人次.但总的出行量即使按照2.5人次/人·日计算，一天也不过500万人次，加之出行分布在空间上的不均匀性，故观测矩阵毫无疑问地会存在很多零元.

由于从出行生成到出行分布的预测分析过程主要是一种乘积运算，这就意味着观测矩阵中的零元将被保持到对未来的估计中去.这明显有悖于常识.为了避免这样的情形出现，实践中有三种可行的方法用以解决这一问题：

（1）部分矩阵法[1]：将含有大量零元的观测矩阵视为部分矩阵来估计参数，而后用模型估计整个矩阵，并将其视为观测矩阵的“真实态”.这种办法显然损失了零元部分的阻抗信息.

（2）补零矩阵法[1]：采用一个较小的数来替换零元.但这样的方法对实际观测矩阵而言，无疑是一种结构上的变形.

（3）增量矩阵法：采用一个全部单元格都为相同较小数的满阵与原观测矩阵相加.显然这种办法能够最大程度地保留原有分布结构.

那么，当面对稀疏矩阵时应该如何选择合理的标定方法就成了交通需求预测理论与实践过程中亟待解决的问题.

重力模型的参数标定并不是一个新问题，早在上世纪70年代Williams I[2]就提出了受Hyman M[3]启发的采用平均阻抗为收敛性判据的参数标定算法，在实际中得到相当广泛的应用.近些年来，随着交通规划建模技术的广泛应用，对一些非常规状态下的重力模型参数标定问题有很多新的研究成果.Lam W等对部分观测矩阵和交通量的组合估计提出了一种随机校准方法[4].Celik M证明了重力模型的标定中小样本观测数据与大样本观测数据同样有效[5].Foulds H.等针对出行矩阵观测数据中的不完备和不精确问题提出了模糊逐次线性逼近的标定算法[6].Guo A等提出了对数线性回归方法用以估计矩阵缺失数据[].这些研究成果都涉及到了实践中出行矩阵的标定问题，但对于城市交通规划中经常遇到的稀疏矩阵问题还缺少与实践相对应的分析成果.实际上在交通规划理论的发展过程中，稀疏矩阵的问题被提出了很长时间[1,8]，但由于实践中重力模型不需要完整的观测数据也能进行标定，所以这一问题在实践中往往被忽视.

本文从重力模型参数估计的有效性和精确性两个不同的效果出发，对出行分布观测数据中的稀疏矩阵问题进行了分析，并通过对重力模型作等价数学规划变换，用拉格朗日乘数法分析了对观测稀疏矩阵的三种不同处理方法的参数估计精确性，最后通过数值计算比较了三种不同处理方法的参数估计有效性.研究结论表明，参数估计的精确性和有效性并不一致，增量矩阵的估计精度最高，但补零矩阵的有效性最好.本文研究结论可以作为实践中观测稀疏矩阵参数标定的理论依据.

2 相关概念界定

为了分析问题，定义真实的出行分布所定义的矩阵结构为“原象”，记为A；通过居民出行调查所得到的观测结果为“观测矩阵”，记为A0；对观测矩阵中原来为零的单元加上小量a后得到的矩阵称为“补零矩阵”，记为A1；对全部单元都加上小量a后得到的矩阵称为“增量矩阵”，记为A2.

那么现在需要比较通过A1和A2标定所得到的重力模型参数与原象矩阵参数的相对关系.但前提条件是双约束重力模型相对于待标定参数而言是单调增的.为了便于问题表述，假定双约束重力模型的阻抗函数为

式中f(xij)为交通小区i到j的交通阻抗，由费用、时间和距离等表达；θ为待定系数.

2.1 重力模型的单调性

按照交通规划理论，一般双约束重力模型可以写为

式中qij为交通小区i到j的估计出行量；Oi为交通小区i的出行发生量；Dj为交通小区j的出行吸引量.

将qij视为关于θ的函数，对式（2）两端求关于θ的导数，得到

考虑到模型的实际意义，显然有Oi＞0，Dj＞0，cij＞0成立.故∂qij∂θ＜0成立.即qij是关于参数θ的单调减函数.

2.2 阻抗函数的一般形式

假设矩阵的所有单元可以划分为两个集合，分别记为S和U.其中S代表观测矩阵中不为0的单元所组成的集合，U代表观测矩阵中为0的单元所组成的集合.则平均费用函数为

式中a和b分别为对非0单元和0单元的调整量，显然有a≥0 a≥0且b≥0b≥0成立.

不妨称式（6）为费用函数的一般形式，容易看出：当a=b=0时为观测矩阵的平均费用函数0，当a=0，b＞0时为补零矩阵的平均费用函数1，当a＞0,b＞0时为增量矩阵的费用函数2.

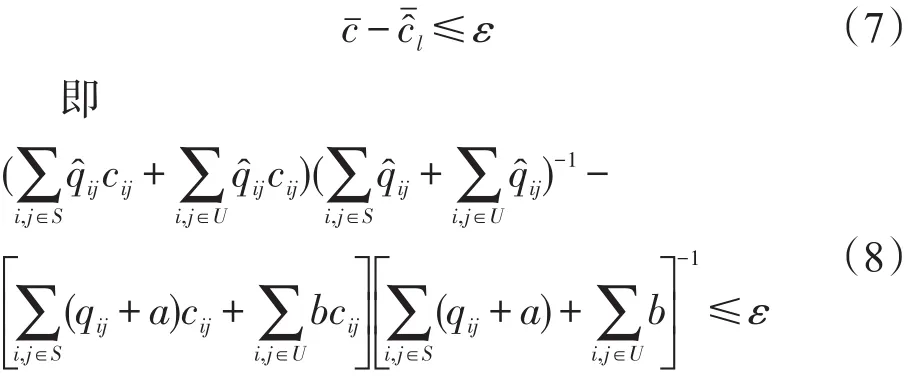
其中，出行量的估计值通过式（9）～式（11）计算得到.

这样就建立了出行观测量与参数之间的关系.

2.3 参数估计有效性和精确性

尽管重力模型的参数标定是依靠迭代求得估计值所对应的估计平均费用与观测平均费用尽量靠近时所对应的参数.然而，通过迭代所得出的参数估计值尽管可能具有较高的精确性，但不一定有对预测工作来说具有有效性.在预测理论中，估计参数的精确性和有效性是两个不同的概念[9].陈华友最早提出了预测有效度概念[10].受此启发，给出估计的精确性和有效性的定义.

定义1参数估计的精确性：将根据对现象的观察所标定的参数值与客观上存在的参数值之间的接近程度定义为参数估计的精确性[11].一般情况下，采用参数的估计值与真值之间的相对距离来表示，即

式中δk为稀疏矩阵的不同处理方法所导致的参数估计误差，下标k为0代表观测矩阵、为1代表补零矩阵、为2代表增量矩阵；为原象矩阵所对应的参数估计值，可以视为参数估计的真值；k为稀疏矩阵的第k种处理方法所得到的参数估计值.

定义2参数估计的有效性：应用参数估计出行矩阵时估计出行量与实际出行量之间的差距[12,13].定义估计的有效性为[14]

式中Δk为稀疏矩阵的不同处理方法所导致的出行量估计误差，下标k为0代表观测矩阵、为1代表补零矩阵、为2代表增量矩阵；tij为原象矩阵第i行、j列的出行量，可以视为矩阵估计的真值；ij,k为稀疏矩阵的第k种处理方法所得到的第i行、j列的出行量的估计值；n为出行矩阵的维数.

3 估计精确性的理论分析

按照交通规划理论，式(2)～式(4)所表达的双约束重力模型与式（14）～式（18）是等价的[15].

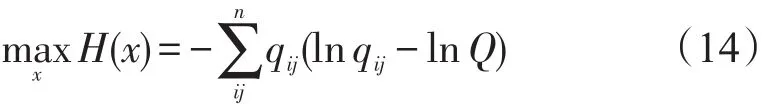
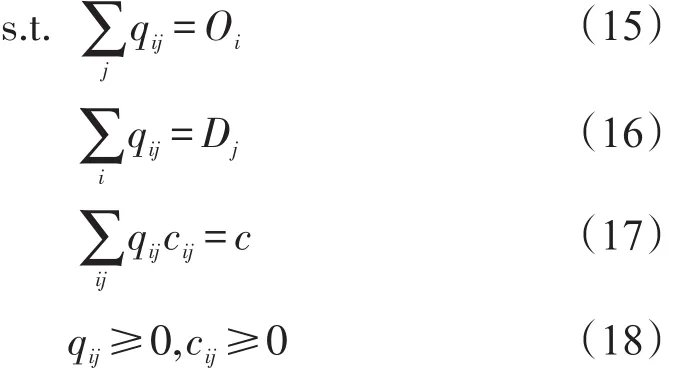
式中Q为出行总量，那么采用拉格朗日乘数法将式(14)～式(18)转化为无约束极值问题，即

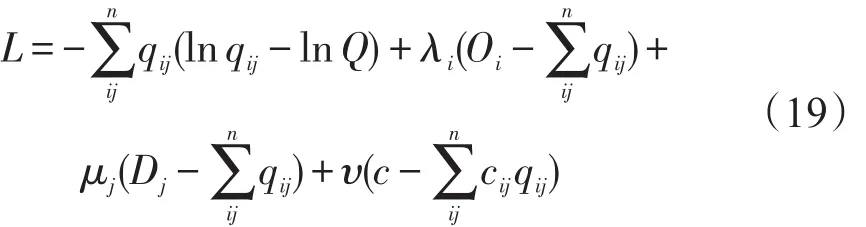
式中λi，μj为拉格朗日系数.

同理，对于观测矩阵而言，其无约束极值问题为

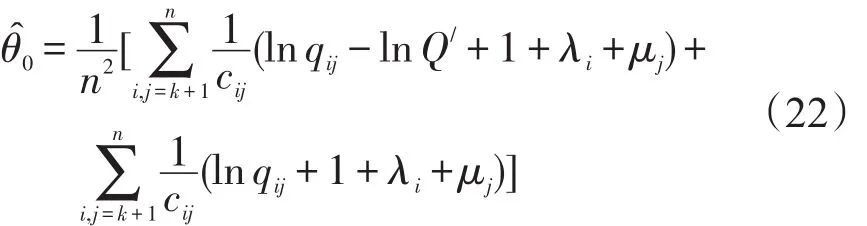
同理，对于补零矩阵而言，其无约束极值

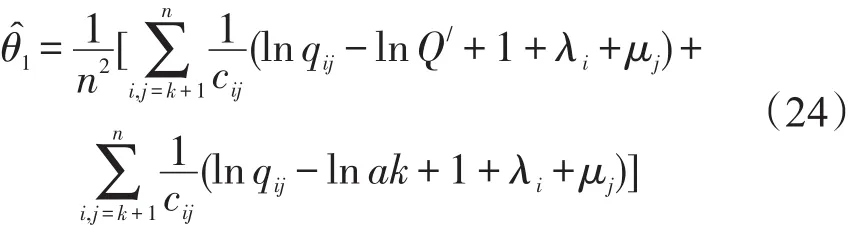
同理，对于增量矩阵而言，其无约束极值问题为

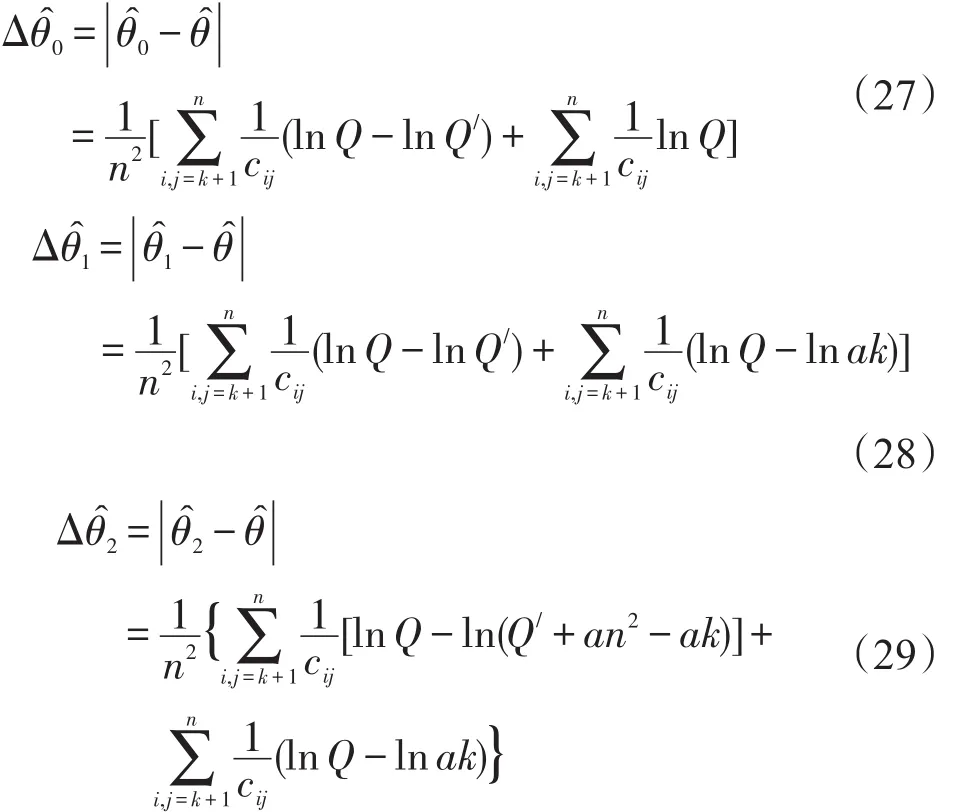
4 估计有效性的数值分析

由于双约束重力模型的结构形式较为复杂，要从解析角度进行参数的有效性估计是十分困难的.但通过数值运算模拟的办法则相对较为可行.借助一个简单的算例来分析稀疏矩阵估计中不同处理方法的有效性差异.

假设有如图1所示的交通小区划分，各小区之间的出行阻抗如表1所示，（观测）部分矩阵为表2，其所对应的出行矩阵原象如表3所示.表4和表5分别为补零矩阵和增量矩阵.

图1 交通小区划分Fig.1 Traffic zone division

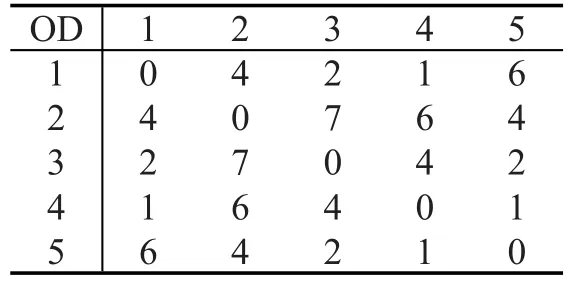
表1 阻抗矩阵Table 1Impedance matrix

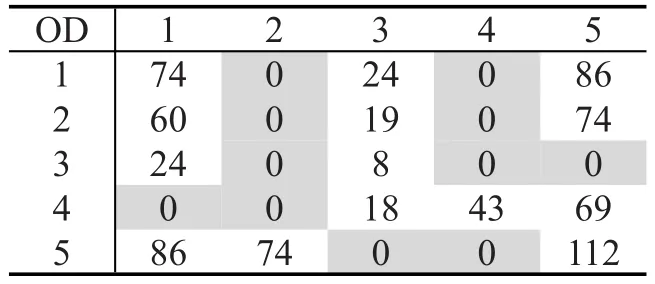
表2 （观测）部分矩阵Table 2Segment matrix(observation)

表3 原象矩阵Table 3The original matrix

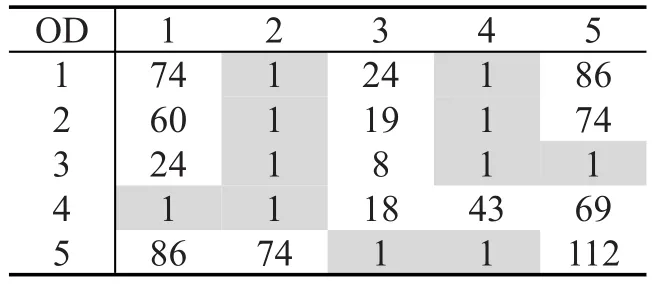
表4 补零矩阵Table 4Zero padding matrix

表5 增量矩阵Table 5Incremental matrix

需要说明的是，对于图1所示的交通小区划分而言，其阻抗是固定不变的，而其原象矩阵可以视为在实际中真实发生的出行分布情况.要了解出行分布状况，就需要对出行的分布进行观测.但需要注意的是，这样的观测往往是不完备的.

按照三种不同的处理方式得到的参数估计结果与原象矩阵的估计结果比较如表6所示.

表6 参数标定结果的精确性比较分析Table 6The accuracy comparative analysis of the calibration results of parameters

在表6中，分别列出了根据原象矩阵、部分矩阵、补零矩阵和增量矩阵分别进行双约束重力模型的标定运算之后的结果，为了比较参数标定的结果，表6中同时也列出了相应于模型参数估计值的平均费用情况.

各个单元格的编号规则如表7所示.为了分析不同参数估计值在矩阵估计中的有效性，将上述依据原象矩阵、部分矩阵、补零矩阵和增量矩阵所估计得到的参数值代入模型当中，并输入阻抗矩阵计算得到各个单元格的估计出行量如表8所示.

表7 各个单元格的编号规则Table 7The numbering rule of each cell

从计算结果上来看，不同参数值的双约束重力模型估计结果表明：采用原象矩阵、部分矩阵、补零矩阵和增量矩阵估计得到的不同参数应用于模型之后所得到的出行矩阵估计效果是不同的.这种差距最主要地表现在估计出行量与实际中真实发生的原象之间的差距上.

从结果上来看，就估计的有效性而言，补零矩阵＞部分矩阵＞增量矩阵.

该结果揭示了重力模型参数标定并不唯一地依赖于对出行现象的观测结果的准确性.除了数据之外，还有一些模型本身的标定算法及计算机存储的舍入等因素对参数标定的结果起着不可忽略的作用[16,17].

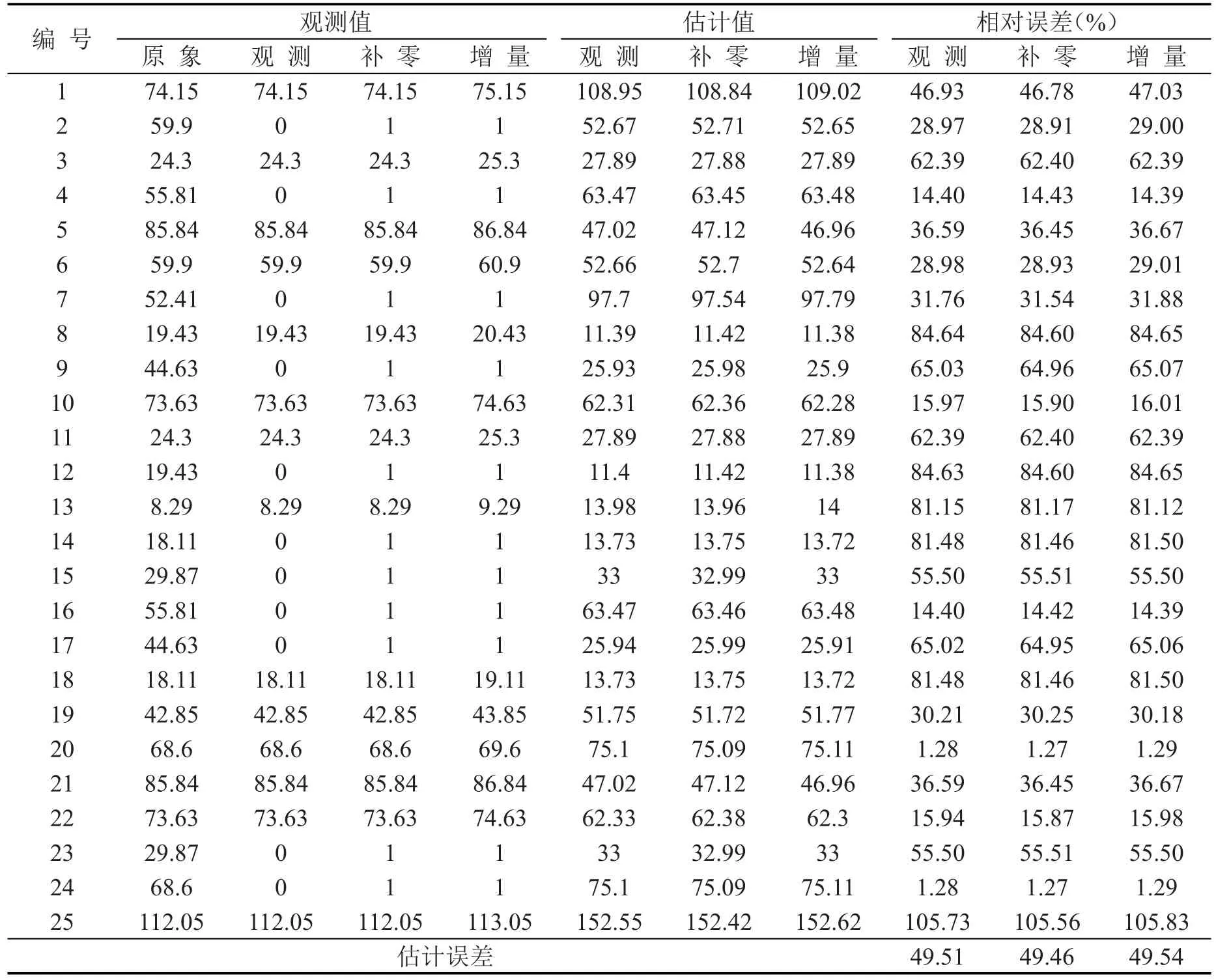
表8 不同参数值的出行矩阵估计结果的有效性分析Table 8The efficiency analysis of the trip matrix estimation results about different parameter values

5 研究结论

本文通过对出行分布观测中常见的稀疏矩阵问题的三种不同处理方式（部分矩阵法、补零矩阵法、增量矩阵法）的比较分析和数值计算，得到以下几点研究结论：

（1）从精确性的角度来看，增量矩阵法相对于补零矩阵法、部分矩阵法具有优势，尽管在数值计算的过程中展现出的优势相对比较微弱.但也有可能随着所研究矩阵的维数增加而表现地更为显著.

（2）从有效性的角度来看，补零矩阵法比增量矩阵法和部分矩阵法更有优势.

（3）虽然本文对稀疏矩阵的处理方法问题作了一定辨析，但依然存在很多尚未解决的问题.例如：不同维数矩阵、不同标定算法结构、不同计算精度要求等情况下三种处理方法的差别等等.这些问题还需要更进一步的分析和研究.

[1]毛保华,曾会欣,袁振洲.交通规划模型及其应用[M].北京:中国铁道出版社,1999.[MAO B H,ZENG H X, YUANZZ.Trafficplanningmodelandits application[M].Beijing:China Railway Press,1999.]

[2]Williams I.A comparison of some calibration techniques for doubly constrained models with an exponential cost function[J].Transportation Research,1976,10(2):91-104.

[3]Hyman M.The calibration of trip distribution models[J]. Environment and Planning,1969,1(3):105-112.

[4]Lam W,Huang H J.Calibration of the combined trip distribution and assignment model for multiple user classes[J].TransportationResearchPartB: Methodological,1992,26(4):289-305.

[5]Celik H M.Sample size needed for calibrating trip distribution and behavior of the gravity model[J].Journal of Transport Geography,2010,18(1):183-190.

[6]Foulds H,Nascimento D,Calixto I,et al.A fuzzy setbased approach to origin-destination matrix estimation inurbantrafficnetworkswithimprecisedata[J]. European Journal of Operational Research,2013,231 (1):190-201.

[7]Guo A,Shen Q,Gizem S.Origin-destination missing data estimation for freight transportation planning:a gravity model-based regression approach[J].General Information,2014,37(6):505-524.

[8]HensherD,ButtonK.Handbookoftransport modelling[M].Oxford,U.K.:Elsevier Science Ltd.,2000.

[9]郎茂祥,傅选义,朱广宇.预测理论与方法[M].北京:清华大学出版社,北京交通大学出版社,2011. [LANG M X,FU X Y,ZHU G Y.Forecasting theory and method[M].Beijing:TsingHua University Press,Beijing Jiaotong University Press,2011.]

[10]陈华友.基于预测有效度的非负变权组合预测模型研究[J].运筹与管理,2001,10(1):48-52.[CHEN H Y. Research on combination forecasting model with nonnegative and time-variant weights based on effective measure of forecasting methods[J].Operations Research and Management Science,2001,10(1):48-52.]

[11]王丽霞.概率论与数理统计:理论、历史及应用[M].大连:大连理工大学出版社,2010.[WANG L X. Probability theory and mathematical statistics:Theory, history and application[M].Dalian:Dalian University of Technology Press,2010.]

[12]陈华友,侯定丕.基于预测有效度的优性组合预测模型研究[J].中国科学技术大学学报,2002,32(2):172-180.[CHEN H Y,HOU D P.Research on superior combination forecasting model based on forecasting effective measure[J].Journal of University of Science and Technology of China,2002,32(2):172-180.]

[13]陈华友,侯定丕.基于标准差的预测有效度的组合预测模型[J].系统工程学报,2003,18(3):203-210+223. [CHEN H Y,HOU D P.Combination forecasting model based on forecasting effective measure with standard deviate[J].Journal of Systems Engineering,2003,18(3): 203-210+223.]

[14]张令刚,牛德宁,孟兆民.基于预测有效度的组合模型在交通量预测中的应用[J].道路交通与安全,2010,10 (1):24-27.[ZHANG L G,NIU D Y,MENG Z M. Application of combination forecasting model based on effective measure in traffic volume forecasting[J].Road Traffic and Security,2010,10(1):24-27.]

[15]刘灿齐.现代交通规划学[M].北京:人民交通出版社, 2001.[LIU C Q.Modern transportation planning[M]. Beijing:China Communications Press,2001.]

[16]陈国强.精密运动控制、设计与实现(原书第2版)[M].北京:机械工业出版社,2011.[CHEN G Q.Precision motion control,the design and implementation(Version 2)[M].Beijing:China Machine Press,2011.]

[17]刘胜.最优估计理论[M].北京:科学出版社,2011. [LIU S.The optimal estimation theory[M].Beijing: Science Press,2011.]

The Sparse Matrix Problem in Trip Distribution Observational Data

LUO Xiao-qiang
（School ofArchitecture,Chang'an University,Xi'an 710061,China）

The problem of sparse matrix in the trip distribution observational data are analyzed,and three different methods are put forward to calibrate the parameters of the double restraint gravitational model,as Parted Matrix Estimation,Zero Replaced Matrix Estimation and Incremental Matrix Estimation.By defining the Estimate Accuracy Index and the Estimate Effectiveness Index to measure the effects of estimation,this paper through the double restraint gravitational model equivalent mathematical programming with constraints,and compares three different analytical method of the estimation precision of the calibration method.On the basis of analysis,it used the methods of numerical simulation calculation,and contrasted the three estimation methods in accuracy and effectiveness.The conclusion finds that the calibration parameters by the method of the Zero Replaced Matrix Estimation have the best results in accuracy,and the calibration parameters by the method of the Incremental Matrix Estimation have the best results in effectiveness.The research results can be used as a theoretical basis of parameters calibration of observation sparse matrix in urban traffic planning in practical.

urban traffic;sparse matrix;parameter calibration;gravity model;error estimation

1009-6744(2015)05-0216-07

U491.1

A

2015-05-21

2015-07-25录用日期：2015-08-11

中央高校基金(2013G1411077)；陕西省社科基金（2014D39）.

罗小强（1979-），男，陕西南郑人，讲师，博士. ＊

luoxq37@yeah.net