例说数学思想在数据收集、整理、描述中的应用

朱志伟

数学是一门非常重要的工具学科，有些学生在学习数学的时候，由于没有掌握好正确的数学学习方法，从而陷入题海，茫然不知所措.如果学生领会数学思想，则可以较快地提高学习质量和数学能力.

一、特殊到一般的思想

例1 （2014·呼和浩特）以下问题，不适合用全面调查的是（ ）

A.旅客上飞机前的安检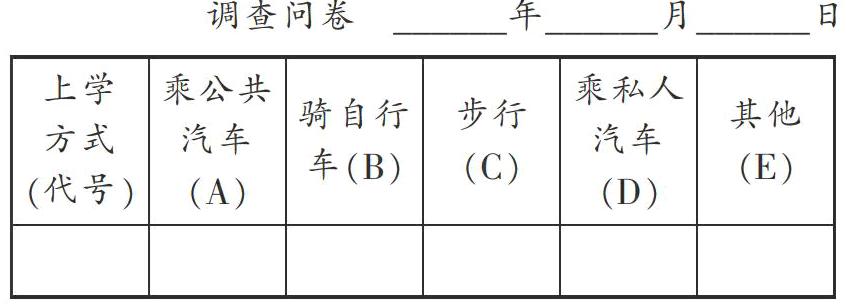

B.学校招聘教师，对应聘人员的面试

C.了解全校学生的课外读书时间

D.了解一批灯泡的使用寿命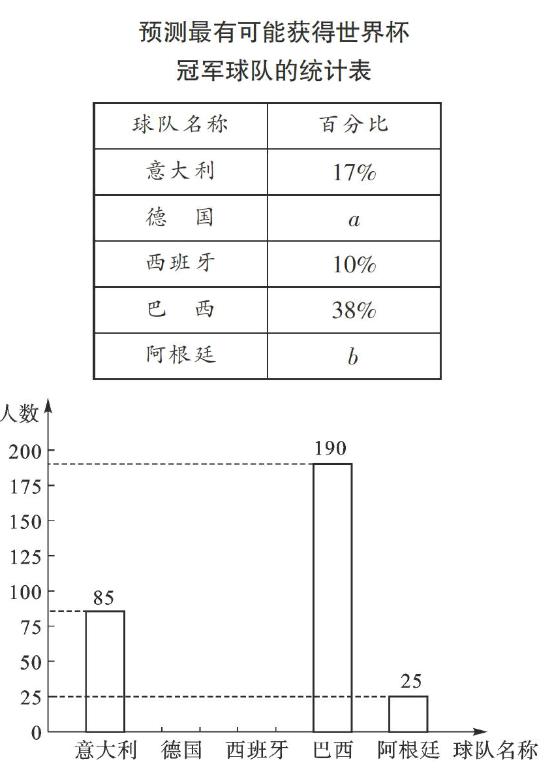

【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似.

【解答】

A、旅客上飞机前的安检，意义重大，宜用全面调查，故此选项错误；

B、学校招聘教师，对应聘人员面试必须全面调查，故此选项错误；

C、了解全校同学课外读书时间，数量不大，宜用全面调查，故此选项错误；

D、了解一批灯泡的使用寿，具有破坏性，工作量大，不适合全面调查，故D选项正确.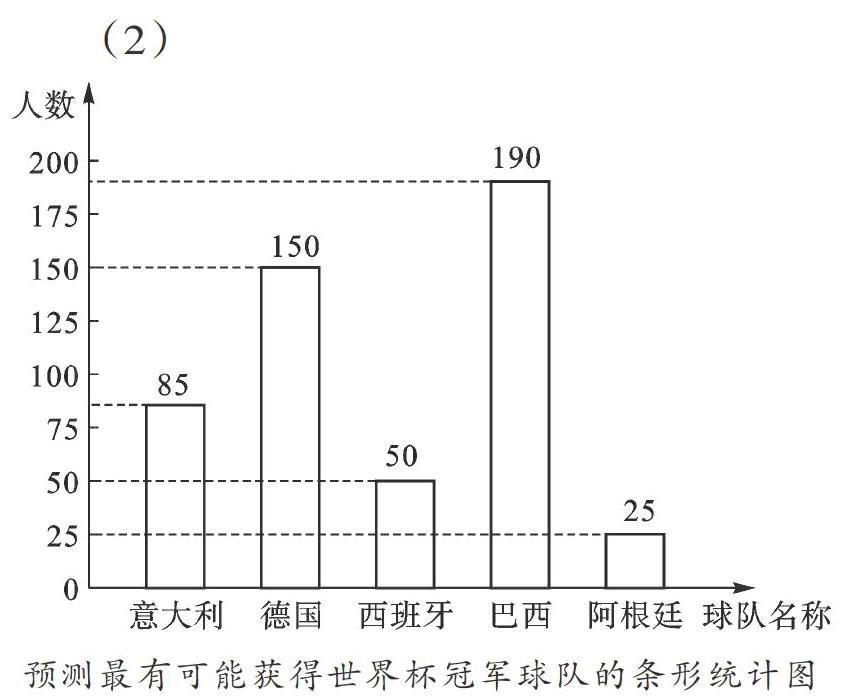

【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查.

例2（2014·青岛）在一个有15万人的小镇，随机调查了3000人，其中有300人看中央电视台的早间新闻.据此，估计该镇看中央电视台早间新闻的约有（ ）

A.2.5万人 B.2万人 C.1.5万人 D.1万人

【分析】求得调查样本的看早间新闻的百分比，然后乘以该镇总人数即可.

【解答】

该镇看中央电视台早间新闻的约有

15× =1.5万，故选B.

【点评】本题考查了用样本估计总体的知识，解题的关键是求得样本中观看的百分比.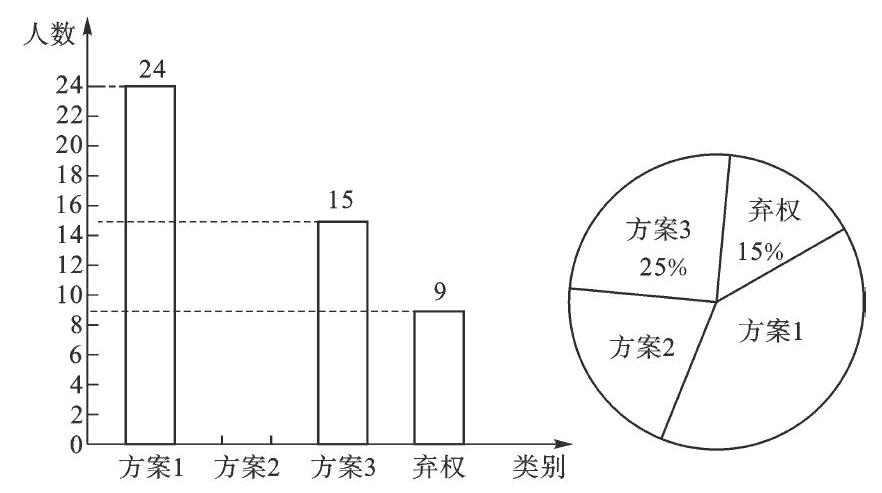

由特殊到一般、由一般到特殊的过程是认识事物的基本过程，数学也不例外.抽样调查，又称抽样推断，是一种重要的、科学的非全面调查方法.它根据调查的目的和任务要求，按照随机原则，从若干单位组成的事物总体中，抽取部分样本单位来进行调查、观察，用所得到的调查标志的数据来推断总体.即抽样调查是根据部分实际调查结果来推断总体标志总量的一种统计调查方法，属于非全面调查的范畴.其中蕴涵了重要的统计思想——样本估计总体.用样本估计总体是特殊到一般的数学思想的一种形式，是本节重点介绍的统计调查方法.

二、分类讨论思想

例3（苏科版八年级下册P10第4题）利用下面的调查问卷对全班同学的上学方式进行调查，并整理调查结果，列出统计表，画出条形统计图.

【点评】这个活动是让学生通过普查的方式去经历收集、整理、描述和分析数据得出结论的统计过程，在经历这个统计调查的过程中，感受统计的思想，建立统计的观念，体验统计的作用，逐步建立用数据说话的习惯.要完成这项活动，学生必须将各种情况分类讨论.如果学生能理解并掌握分类讨论的思想方法，在解题中进行正确、合理、严谨的分类，这既有利于把复杂的问题转为简单的问题来处理，同时也可以培养学生的综合分析能力和发展他们思维的条理性、严谨性和完整性.

三、数形结合思想

我国著名的数学家华罗庚说过“数缺形时少直观，形无数时难入微”，这是对数形结合思想的高度概括.数形结合培养学生的空间观念和数感，是使学生进行形象思维与抽象思维互相促进，和谐发展的主要形式；数形结合教学又有利于培养学生灵活运用知识的能力.

例4（2014·辽宁沈阳）2014年世界杯足球赛于北京时间6月13日2时在巴西开幕，某媒体足球栏目从参加世界杯球队中选出五支传统强队：意大利队、德国队、西班牙队、巴西队、阿根廷队，对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效，每位被调查者只能填写一份问卷，在问卷中必须选择这五支球队中的一队作为调查结果，这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计，绘制了统计图表的一部分如下：

（2）根据以上信息，请直接在答题卡中补全条形统计图；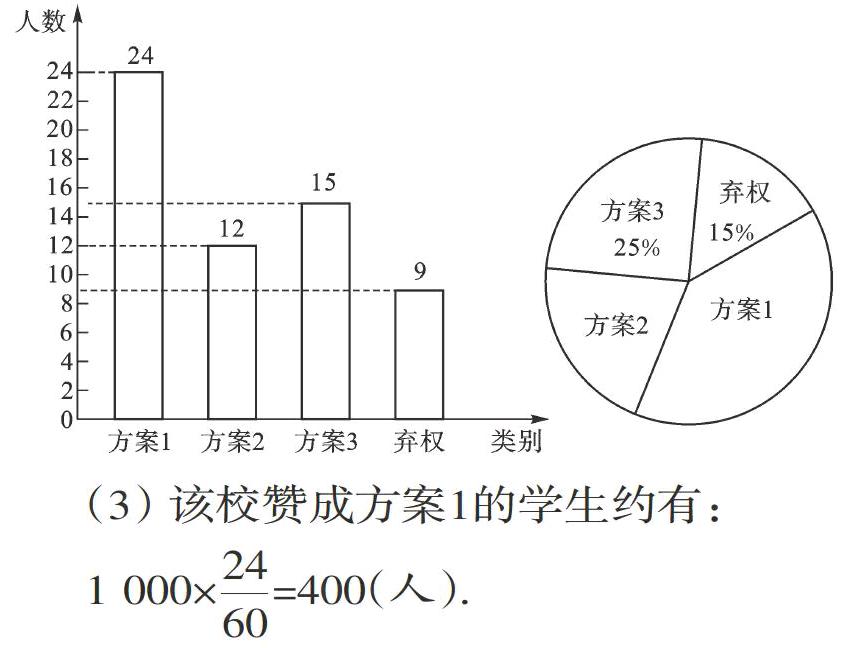

（3）根据抽样调查结果，请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.

【分析】（1）首先根据意大利有85人，占17%，据此即可求得总人数，则根据百分比的定义求得b的值，然后利用1减去其它各组的百分比即可求得a的值；

（2）根据百分比的定义求得德国、西班牙的人数，即可解答；

（3）利用总人数4800，乘以对应的百分比即可求解.

【点评】本题考查的是条形统计图的综合运用.读懂统计图，从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.

例5 （2014年广西钦州）某校为了解学生对三种国庆活动方案的意见，对该校学生进行了一次抽样调查（被调查学生至多赞成其中的一种方案），现将调查结果绘制成如图两幅不完整的统计图.

请根据图中提供的信息解答下列问题

（2）请把条形统计图补充完整；

（3）已知该校有1000名学生，试估计该校赞成方案1的学生约有多少人？

【分析】（1）根据赞成方案3的有15人，占25%，据此即可求得调查的总人数，利用360°乘以对应的比例即可求得图中方案1所对应的圆心角的度数；

（2）利用总人数减去其它各组的人数，即可求得赞成方案2的人数，从而作出直方图；

（3）利用总人数1000乘以对应的比例即可求解.

【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小.

总之，数学思想方法只有在反复的运用中才能被学生所熟悉掌握，这需要数学教师有意识的渗透到平时的教学之中.一旦学生领悟到这些数学思想方法的内涵与真谛，将会更深刻地理解知识，灵活运用知识解决问题，从而形成分析、解决问题的能力.就像日本著名数学教育家米山国藏曾说的：“我搞了多年的数学教育，发现学生在初中、高中阶段学习的数学知识……离校后不到一二年，便会很快遗忘掉了.然而无论他们从事什么工作，唯有深深铭刻于头脑中的数学精神、数学思维方法、研究方法……却随时随地发生作用，使他们受益终生.”

（作者单位：苏州市吴江区实验初级中学）