振动对带肋通道内流动与传热影响的数值模拟
宋 平,沈佳欢,王宏光
(上海理工大学能源与动力工程学院,上海市动力工程多相流动与传热重点实验室,上海200093)
现代燃气轮机涡轮进口的燃气温度已远远高于叶片材料的承受极限,涡轮叶片需要进行冷却,其中肋片强化传热被广泛用于涡轮叶片内部对流冷却[1-3].涡轮的动叶片在实际工作中由于受到静叶尾迹和转子不平衡[4]等因素的激励,工作在小振幅高频率的振动状态[5].叶片振动可以使其内部冷却流体产生扰动,对强制对流换热产生影响[6].Faircloth等[7]通过实验研究了水平圆柱的水平振动,结果表明:振动雷诺数高于临界值时,瞬时对流传热系数增大20%~30%.Rishema等[8]采用数值方法分析了竖直振动对圆柱外部绕流换热的影响,结果表明:振动能强化换热.宿艳彩等[9]采用数值方法模拟了振动方向对圆柱外部绕流传热的影响,结果表明:振动方向对圆柱外部绕流传热的影响不大,而振动速度远大于来流速度时,振动强化换热效果显著.姜波等[10]结合数值分析和实验研究了低频振动管外流动与传热特性,结果表明:振动有利于强化换热.王一平等[11]通过实验研究了流体低速错流流过振动平板的传热特性,结果表明:振动能有效强化换热,与频率相比振幅对传热的影响较大.吴艳阳等[12]运用Fluent软件分析了圆管在振动条件下管内流体的流动与传热特性,结果表明:在同一振动参数下,雷诺数越小,强化传热效果越好;对每一来流速度,存在临界振幅和频率,低于临界值不能强化传热.这些研究表明,在一定的条件下,换热面振动对对流传热有强化作用,强化传热效果主要与主流速度、振动频率和振幅有关.因此,笔者采用数值模拟方法研究叶片振动对叶片内部带肋通道流动和换热的影响.
1 计算模型及边界条件
1.1 计算模型
以Han等[3]所研究的叶片内部对流冷却实验模型为基础,为减少计算量,将该几何模型简化为二维模型,并对入口段和出口段适当延长,如图1 所示.正方形肋片边长e=2.38mm,肋间距P=10×e=23.8mm,入口高度Hi=152.4 mm,出口高度Ho=50.8mm,实验段长Lm=211.82mm,入口段长Li=305 mm,出口段长Lo=711.2 mm,O点坐标为(0,0).运用ICEM 软件对计算区域划分网格,采用四边形结构化网格,对靠近壁面处进行加密,经过网格无关性验证,网格总数大于103 400时,网格密度对计算结果影响不大,此时靠近壁面第一层网格高度为1.3×10-2mm.
1.2 边界条件及求解设置

图1 简化后的几何模型Fig.1 Simplified geometry model
使用Fluent软件,采用标准k-ε模型,近壁面采用scalable-wall的处理方式.流体为不可压缩空气,空气参数如下:密度ρ=1.225kg/m3,黏度μ=1.789×10-5kg/(m·s),导热系数λ=0.242 W/(m·K),比定压热容cp=1 006.43J/(kg·K).肋片材料为铜,密度ρCu=8 978kg/m3,比定压热容cp,Cu=381J/(kg·K),导热系数λCu=387.6 W/(m·K).对肋片内部导热与表面对流传热进行耦合传热分析;肋片与空气的交界面设为耦合壁面,OP和MN壁面给定热流密度q,其余壁面设置为绝热壁面;入口给定流体速度与温度,出口给定静压为0Pa.
1.3 参数定义
为进行数据处理与分析,定义实验段入口、出口温差为
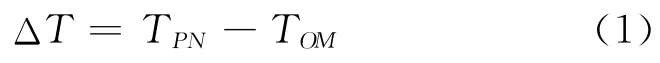
忽略热辐射和流动耗散产生的热量,由能量守恒有
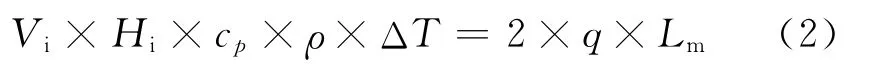
实验段空气平均温度为

对流传热系数为

式中:Tw为壁面温度.
Nu定义如下:
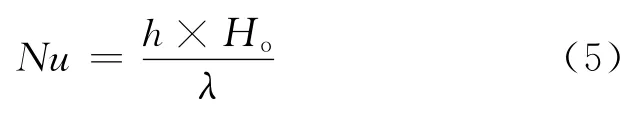
为表征振动对流动阻力的影响,定义入口静压波动值Δp为
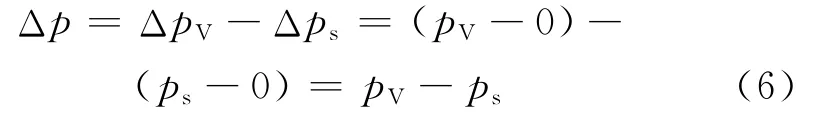
式中:pV为壁面振动时入口流体瞬时静压;ps为稳态(壁面不振动)时入口流体瞬时静压.
2 计算结果及分析
2.1 稳态壁面计算结果
分别对Re为1×104和3×1042个工况(工况条件分别见表1和表2)进行了稳态数值模拟,模拟结果与Han等[3]实验结果的比较见图2和图3.由图2和图3可以看出,在第3个肋片以后模拟结果与实验结果吻合较好.前2个肋片偏差较大是由于模型从三维简化为二维后前台阶对流动的影响减弱造成的.忽略前2个肋片后,相对于实验结果,模拟结果误差在20%以内,表明计算模型的选择以及边界条件的设置合理.

表1 Re=1×104 时壁面的边界条件Tab.1 Boundary conditions of stationery wall for Re=1×104
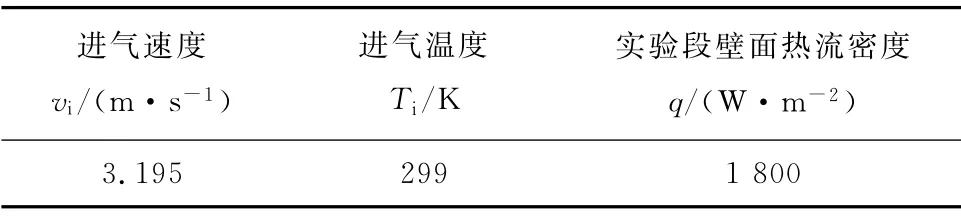
表2 Re=3×104 时壁面的边界条件Tab.2 Boundary conditions of stationery wall for Re=3×104
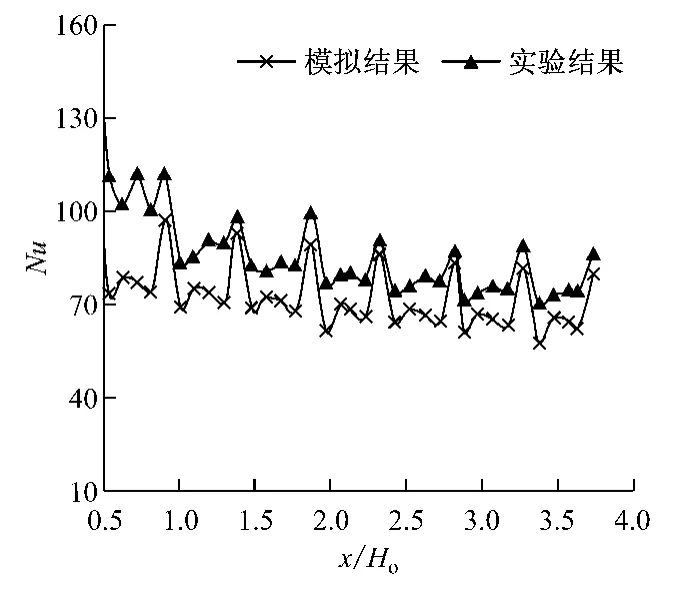
图2 Re=1×104 时模拟与实验Nu的比较Fig.2 Comparison of Nubetween simulation results and experimental data,Re=1×104

图3 Re=3×104 时模拟与实验Nu的比较Fig.3 Comparison of Nubetween simulation results and experimental data,Re=3×104
2.2 振动壁面计算结果
设实验段做Bo型振动[13],则肋片跟随壁面振动,设定上、下2个壁面做同相位振动,实验段的振型如图1中虚线所示,壁面振动位移方程为

式中:y为壁面振动位移;f为振动频率;A为壁面最大振幅;x为振动位置的x坐标.
壁面振动通过Fluent UDF 编程实现,边界条件如表3所示.

表3 振动壁面的边界条件Tab.3 Boundary conditions of vibration wall
图4给出了A=2mm、f=2kHz、Re=3×104、x/Ho=1.985 处上、下壁面的Nu.由图4 可以看出,Nu随时间呈周期性变化,变化周期与壁面振动周期一致.
定义振动时换热效果时均值为:

定义换热增长率[8]为

式中:Nus为稳态时的Nu.
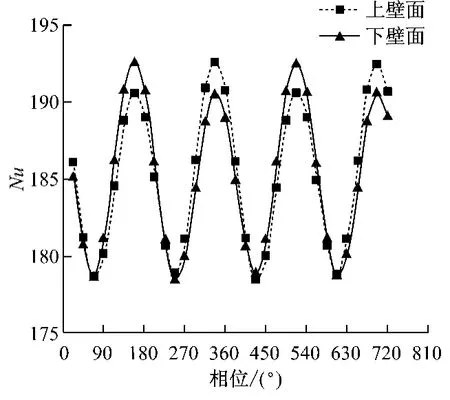
图4 上、下壁面Nu的比较Fig.4 Comparison of Nubetween upper and lower part of wall
2.2.1Re的影响
分析壁面振动时不同入口速度对换热的影响.分别取实验段Re为5×103、1×104、2×104和3×104,对应入口速度分别为0.532 5m/s、1.065m/s、2.15m/s和3.195m/s,边界条件如表3所示.图5给出了不同Re对换热的影响.由图5可以看出,Re越大,振动强化传热效果越不明显,这是由于入口速度越大,振动造成的扰动相对于无振动时的扰动越小,此结果与文献[9]中的结果吻合.图6给出了不同Re下壁面振动造成的入口、出口静压差值的变化.由图6可以看出,Re越大,入口静压波动幅度越大,且其峰值相位相对于振动峰值相位也逐渐超前.

图5 不同Re对换热的影响Fig.5 Effect of Re on heat transfer
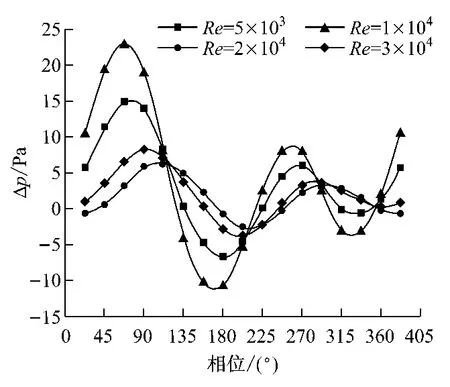
图6 振动时不同Re对静压差值的影响Fig.6 Effect of Re on static pressure in vibration case
2.2.2 相同振动强度时振幅(或频率)的影响
分析相同振动强度(A×f=4m·Hz)下,不同振幅(或频率)对流动与换热的影响.振幅A分别为0.5mm、1.0mm、1.5mm 和2.0mm,对应的频率分别为8kHz、4kHz、2.67kHz和2kHz,边界条件见表3.图7给出了Numax-Numin沿流向的变化.图8给出了相同振动强度下不同A对换热的影响.由图7可知,振幅A越大,振动引起的换热波动越小.由图8可知,振幅A越大,换热强化效果越不明显;当A>1.5mm 时,振幅增大对换热的影响不明显,总体上振动强化了换热,但是由于肋片扰流的作用,局部区域可能出现抑制换热的情况.图9为在相同振动强度下,不同A对入口静压差值的影响.由图9可以看出,随着振幅的增大,入口静压波动幅度增大,其原因是振幅越大,壁面振动引起的流道变化越剧烈,导致流动阻力的变化越剧烈,即入口静压波动越剧烈.
3 结 论

图7 Numax-Numin沿流向的变化Fig.7 Change of Numax-Numinalong flow direction
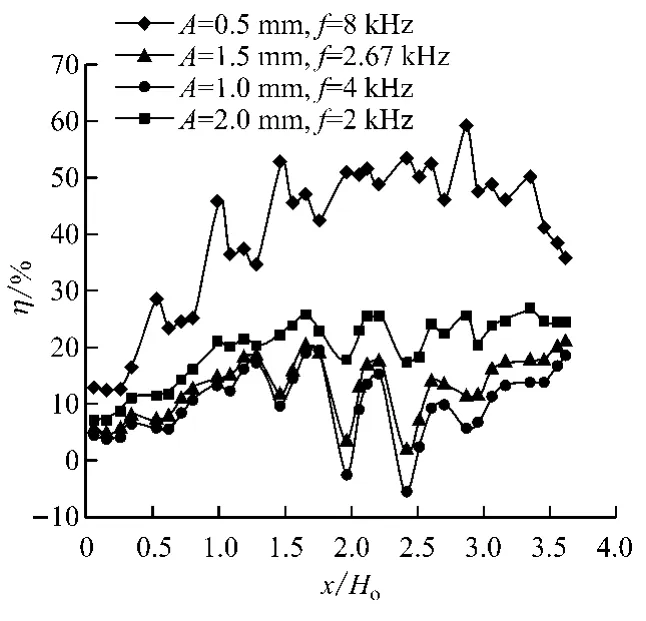
图8 相同振动强度下A 对换热的影响Fig.8 Effect of Aon heat transfer at same vibration intensities

图9 相同振动强度下A 对入口静压差值的影响Fig.9 Effect of Aon static pressure at same vibration intensities
(1)在壁面振动条件不变时,Re越大,振动引起的扰动相对于主流速度就越小,从而导致强化换热效率越低;壁面振动导致近壁面流体产生横向运动速度,形成流阻和主流速度的周期性变化,引起入口静压波动,且其峰值相位相对于振动峰值相位逐渐超前.
(2)在相同振动强度下,振幅越大,振动引起的换热波动越小,换热强化率越低;当A>1.5 mm时,振幅增大对换热的影响不明显;振幅越大,壁面振动引起的流道变化越剧烈,导致入口静压波动越剧烈.
(3)总体上振动可以强化换热,但是随着Re和振幅的增大,局部区域会抑制换热.
[1]HAN J C,PARK J S.Developing heat transfer in rectangular channels with rib turbulators[J].International Heat and Mass Transfer,1988,31(1):183-195.
[2]HAN J C,PARK J S,LEI C K.Heat transfer enhancement in channels with turbulence promoters[J].Journal of Engineering for Gas Turbines and Power,1985,107(3):628-635.
[3]HAN J C.Heat transfer and friction characteristics in rectangular channels with rib turbulators[J].ASME Journal of Heat Transfer,1988,110(2):321-328.
[4]张艾萍,谢媚娜,林圣强.椭圆滑动轴承油膜厚度对汽轮机振动的影响[J].动力工程学报,2013,33(9):677-681.
ZHANG Aiping,XlE Meina,LIN Shengqiang.Effect of oil film thickness of elliptic sliding bearing on steam turbine vibration[J].Journal of Chinese Society of Power Engineering,2013,33(9):677-681.
[5]艾书民,王克明,廖辉,等.稳态温度场作用下涡轮叶片振动特性的研究[J].沈阳航空航天大学学报,2011,28(4):17-21.
AI Shumin,WANG Keming,MIAO Hui,etal.Research on turbine blade vibration characteristic under steady state temperature field[J].Journal of Shenyang Aerospace University,2011,28(4):17-21.
[6]RICHARDSON P D.Effects of sound and vibrations on heat transfer [J].Applied Mechanics Reviews,1967,20(3):201-217.
[7]FAIRCLOTH J M,SCHAETZLE W J.Effect of vibration on heat transfer for flow normal to a cylinder[J].Journal of Heat Transfer,1969,91(1):140-144.
[8]RISHEMA M,AL-HAFIDH M H.The effect of longitudinal vibration on laminar forced convection heat transfer in a horizontal tube[J].Journal of Engineering,2006,13(3):863-879.
[9]宿艳彩,葛培琪,闫柯,等.流体绕流不同方向振动圆柱换热特性数值分析[J].振动与冲击,2011,30(10):221-223.
SU Yancai,GE Peiqi,YAN Ke,etal.Heat transfer characteristic of a vibrating cylinder with fluid flow[J].Journal of Vibration and Shock,2011,30(10):221-223.
[10]姜波,田茂诚,冷学礼,等.低频振动管外流动与传热特性研究[J].工程热物理学报,2009,30(5):811-813.
JIANG Bo,TIAN Maocheng,LENG Xueli,etal.Research on flow and heat transfer characteristics outside flow frequency vibration tubes[J].Journal of Engineering Thermophysics,2009,30(5):811-813.
[11]王一平,卢艳华,朱丽,等.振动平板的传热性能实验[J].天津大学学报,2010,43(6):549-552.
WANG Yiping,LU Yanhua,ZHU Li,etal.Experiment on heat transfer performance of vibrating plate[J].Journal of Tianjin University,2010,43(6):549-552.
[12]吴艳阳,刘利军,喻九阳,等.振动圆管内对流传热特性及场协同分析[J].石油化工设备,2011,40(6):1-5.
WU Yanyang,LIU Lijun,YU Jiuyang,etal.Convective heat transfer characteristics and field synergy analysis inside vibration circular tube[J].Petro-Chemical Equipment,2011,40(6):1-5.
[13]华东电力试验研究所.汽轮机叶片的振动特性和调整[M].北京:电力工业出版社,1981:63-67.

