汽车装配车间物流超市分散化程度决策模型研究

王 叶，张 镓，蔡三发

（同济大学 经济与管理学院，上海 200092）

汽车装配车间物流超市分散化程度决策模型研究

王 叶，张 镓，蔡三发

（同济大学 经济与管理学院，上海 200092）

基于物流成本最小化角度，分析了物流超市在汽车装配车间的分散化程度与成本结构中各部分之间的关系，引入多生产线分组的概念，构建物流超市分散化程度决策模型。

物流超市；分散化程度；物流成本；多生产线；汽车装配车间

1 前言

随着消费者对汽车多样性的需求越来越大，汽车行业装配生产对汽车物流的实时性和准确性要求也越来越高。由于汽车生产具有小批量、多频次的特点，同时汽车生产需要上千种零配件，越来越多的汽车生产企业引入JIT策略来进行场内物流管理。物流超市应运而生。

物流超市，狭义的来说，是分散在装配车间，临近生产线旁，服务于临近生产线的零部件存储区域。但近年来，随着物流超市在汽车装配生产中的应用和发展，物流超市逐渐衍生出了卸货、捡货、备货、排序、返空箱、订货、物料上线配送以及破损物品返修等功能。与传统场内物流相比，物流超市可以实现更短的交付时间，更稳定的交付能力（货箱大小固定，运输叉车时间固定），更快的订单响应速度，更灵活的应对变化。

正是由于物流超市存在诸多优点，近年来国内外学者逐渐开始关注研究物流超市。国外对物流超市的研究主要集中在装配企业对物流超市的应用研究。其中，Persom A（2007）[1]认为，装配企业需求的零部件众多，对库存安排提出了更高的要求。Daria Battini（2010）[2]研究了在装配企业内部多生产线条件下，物流超市的最优数量与分布问题。Akcay Y（2004）[3]研究了在集中库存基础上，物流超市的分散库存对生产的保障作用。Golz（2011）[4]研究了物流超市操作人员的数量和每个操作员负责装配线的数量，以及在超市中的活动路径。Emde和Boysen（2012）[5]研究了物料运作调度问题。国内学者对于物流超市的研究还停留在定性分析层面，并没有从定量角度分析物流超市的布局优化。其中，郑秀恋和刘陆（2013）[6]分析了传统汽车生产物流面临的问题，把物流超市引入汽车生产物流中，并提出物流超市数量和位置的设定应该遵循与生产线相适应的原则。他们认为物流超市的位置可以位于生产区域，或者直接设置在生产线旁。俞杰（2004）[7]以某工厂为实例介绍了物流超市的具体定义，研究了物流超市在工厂内的具体实施情况和实施效果。

从国内外的研究成果中可以看出，目前学术界对物流超市分散化程度的研究还比较匮乏，而物流超市分散化程度对汽车装配生产效率的影响是不容小觑的。因此，本文从成本角度入手，研究以降低成本为目标的物流超市分散化程度决策模型。

2 物流超市分散化问题的主要矛盾

2.1 装配车间内物流超市相关成本分析

装配车间内物流超市的分散化程度主要关系到物流超市的数量，以及各物流超市与所服务的生产线间的距离，即物流超市的位置。汽车装配车间的物流生产目标是降低成本，因此衡量物流超市分散化程度优劣的主要标准是物流总成本的多少。本文中，对于汽车装配车间中物流总成本，主要考虑四个方面：存货成本、投入与运营成本、运输成本以及缺货风险成本。了解这四类成本与物流超市分散化程度的关系，就能找出解决问题的关键。

存货成本。物流的存货成本，指由于货物的存储造成的物流费用增加。在本文中，物流超市中的存货主要指用于汽车装配生产的汽车零配件。基于物流超市的功能，超市中存储的零配件主要用于满足短时间内的装配生产需求。由于物流超市中的零部件存储满足实时性的特点，因此超市中各零部件的存储量普遍较小。超市中各零部件的存储量需满足最小安全库存量的要求。因此，当物流超市的数量增加时，相应的满足装配生产的所有汽车零部件总库存量相应增加，导致物流存货成本增加。简单的来说，当同一零部件供应不同的装配生产线时，服务于生产线的物流超市数量越多，该零部件在物流超市中的总库存量越大，库存成本越高。即物流超市分散化程度越高，则物流超市存货成本越高。

投入与运营成本。物流超市的建设初期需要投入大量的人力和物力，这就造成了一部分固定成本。显然，当物流超市的数量增加时，总建设成本会增加。与此同时，基于物流超市的功能，如卸货、拣货、配货以及物料配送上线等，这些都需要一定数量的运作工具以及运作人员。并且，物流超市的数量越多，装配车间对其运作越复杂，产生的间接运作成本越高。因此，物流超市数量的增加同样会导致投入与运营成本的增加。即物流超市分散化程度越高，则物流超市的投入与运营成本越高。

运输成本。顾名思义是由于汽车零部件从物流超市配送到生产线旁而引起的成本。这主要受运输距离的影响。因此，物流超市距离生产线越近，零部件的物流运输总成本越小。而物流超市数量越多，允许的与生产线的距离越近，运输成本越低。即物流超市分散化程度越高，则物流超市的运输成本越低。

缺货风险成本。汽车装配生产是一项系统化，综合性的生产运作。因此，任何生产环节的问题都将影响整个装配生产线的运作情况。汽车零部件能否及时准确的配送到相应的生产线旁，是保证生产安全稳定的关键之一。因此，当物流超市数量越少，导致零部件在物流超市中的总库存量变小时，其应对突发事件的能力越弱，存在的缺货风险成本越高。即物流超市的分散化程度越高，则物流超市的缺货风险成本越低。

2.2 分散化问题关键点

根据上一小节物流超市成本结构分析可知，物流超市的总成本包括：存货成本、投入与运营成本、运输成本以及缺货风险成本公式（1）。其中，存货成本、投入与运营成本，与物流超市分散化程度呈正相关关系；而运输成本、缺货风险成本，与物流超市的分散化程度呈负相关关系。这种关系可以粗略的描述为图1的情况。从图中分析可知，如何平衡两者情况的成本，是决定物流超市分散化程度的关键。

总成本=存货成本+投入与运营成本+运输成本+缺货风险成本（1）

图1 物流超市分散化程度与成本关系图

3 物流超市分散化程度决策模型

3.1 模型描述与假设条件

在构建物流超市货架决策模型前，需要引入一些变量，并对模型中出现变量的涵义以及变量间的简单关系进行明确的解释。与此同时，由于分析模型的构建必然存在一些合理的理想化分析，因此，本文有必要交代清楚模型的假设条件。

（1）变量描述及变量关系

其中，CW为物流超市总成本，CI为物流超市所有零部件总库存成本，CBO为物流超市投入与运营成本，CT为物流超市总运输成本，CR为物流超市缺货风险成本；Pi：汽车零部件种类i，其中i=1,...,N；Lj：汽车装配生产线 j，其中 j=1,...,M；Ui,j：单位时间内汽车零部件i在汽车装配生产线 j中的平均需求量；σi,j：单位时间内汽车装配生产线 j对汽车零部件i平均需求量的标准差。

Ui：单位时间内汽车零部件i在所有汽车装配生产线中的总平均需求量。

σi：单位时间内汽车零部件i在所有汽车装配生产线中总平均需求量的标准差，其中，模型假设每种零件平均需求量之间相互独立；Ki：汽车零部件i的单次运输容量；Ci：汽车零部件i的单位成本；ti：汽车零部件i的库存成本指数，在本文中这些库存成本为Ci的一定比例ti，即零部件i的单位库存成本等于tiCi。

SSi,j：单位时间内汽车零部件i在汽车装配生产线 j中的安全库存量[8];ki,j：表示零部件i满足生产线 j的安全库存量，由服务水平决定；σi,j：单位时间内汽车装配生产线 j对汽车零部件i平均需求量的标准偏差，该需求量服从正态分布；LTi,j：补货提前期，即从汽车装配生产线 j发出指令，到汽车零部件i配送到生产线的时间，由于是短距离运输，这里假定每种汽车零部件i的补货提前期相同；(x,y)：汽车装配生产线及物流超市货架的分布坐标。在本文的模型中，把生产线与超市置于二维平面中，生产线的位置是固定的，物流超市货架的位置是非固定的。但是，物流超市货架的位置不是随机的，而是离散的存在于生产线旁的几个可选位置中，货架位置数量取值为1,...,M。

d( ) Lk,Wq：固定位置的装配生产线Lk与固定位置的物流超市货架Wq的距离，其中，q是物流超市货架W的位置选择之一。

（2）模型假设

假设1：一个汽车装配生产车间内存在多条生产线，并且生产线间存在一定的零部件共用情况。

假设2：对于一条固定的装配生产线，其需求的每种零部件来自于唯一的物流超市，通常情况下为距离最近的物流超市。换句话说，每一条装配生产线由单一物流超市供应零部件。

假设3：在给定距离下的运输成本由运输距离和单位运输费用决定。

其中，C0表示单位距离的运输成本，通常由运输工具的年采购与维修成本和年运营成本决定。

假设4：由于物流超市的分散化程度对订货成本的影响不大，因此本模型中不予考虑。

假设5：当物流超市服务于单一生产线时，物流超市位于该生产线旁；当物流超市服务于多生产线时，物流超市位于若干生产线中间位置。即物流超市服务的生产线固定，则物流超市在装配生产车间中的位置固定。

3.2 模型构建

物流超市的分散化程度即为确定物流超市的数量和位置。从假设5中可以看出，物流超市的数量直接影响了物流超市的位置，所以该决策模型的首要目的是确定物流超市的数量。同时，从第三节可以看出，物流超市的数量直接影响物流成本，而决策模型的目标是使物流总成本最小。这就可以找到两者间的关系，确定决策模型。

（1）生产线分组。本文引入生产线分组的概念。所谓生产线分组，即根据生产线间的相似度，把相似度较近的生产线划归为同一组，从而可以为每组生产线安排一个物流超市。而本文中，由于相似度标准不同，从而产生不同的分组情况，即不同的物流超市分散化程度。

其中，ni,j表示生产线i和生产线 j之间相同零部件数量，Ni，Nj分别表示生产线i和生产线 j所需的所有零部件数量。 ηi,j表示生产线 i和生产线 j之间的相似度，且0≤ηi,j≤1.ηi,j越接近1，两条生产线间的相似度越高；反之，两条生产线间的相似度越低。当ηi,j为0时，表示两条生产线间完全不存在共用的零部件；当ηi,j为1时，表示两条生产线所需的零部件完全相同。

根据相似性程度，把多条生产线分成G组，其中G=1,2,...,M。同时，生产线的分组遵循相近原则，即当一条生产线与其他若干条生产线间的相似度相同时，选距离该生产线最近的生产线与其组成一组。

（2）计算库存成本。由于库存成本与零部件的安全库存量和单位库存成本相关，根据这样的关系，可以首先计算每个分组的库存成本如下：

其中，Cp表示由于分组p中各生产线对零部件的需求而引起的库存成本；则所有分组的总库存成本计算如下：

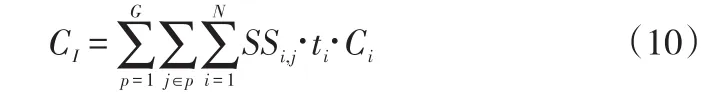
（3）计算投入与运营成本。由于投入与运营成本仅简单与物流超市的数量有关，因此计算如下：

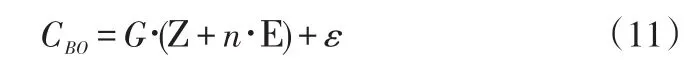
其中，Ζ表示单个物流超市的建设投入成本，Ε表示每年的运营成本，包括管理成本、存储设施维护成本等。n为运营年限，这里以10年记。ε为由于忽略等原因造成的偏差估计。

（4）计算运输成本。在确定不同数量前提下的装配生产线最优分组情况后，需要为每个最优分组确定相应的物流超市货架位置。物流超市货架与其供货的装配生产线的相对位置，决定了运输成本的大小。因此，运输成本最小化可以作为决定最优位置的标准。

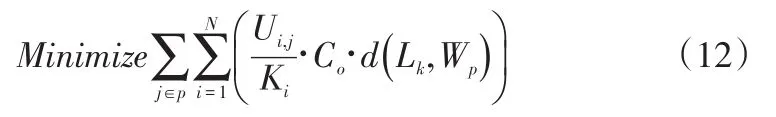
其中，Wp为服务于生产线分组p的物流超市货架位置。这里，分组p的装配生产线的位置是固定的。生产线与物流超市货架间的距离用公式（6）计算，运输成本的计算参考公式（7），Ui,j表示一定时间内零部件i在装配生产线 j中的平均使用率，Ki表示汽车零部件i的单次运输容量。

则所有分组的运输成本计算如下：

（5）计算缺货风险成本。物流超市的缺货风险成本主要与汽车零部件的安全库存量相关，库存量越低，则存在的缺货风险越高。因此，物流超市的缺货风险成本计算如下：

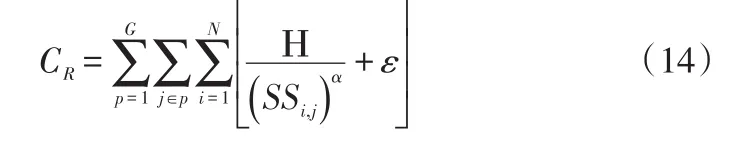
其中，α为影响因子，是大于等于1的系数固定值参数，Η为单位缺货风险成本，ε为由于每种汽车零部件的安全库存量对缺货风险影响的偏差估计。

（6）目标函数。本文对于物流超市分散化决策模型的研究是基于物流成本考虑的。因此，该决策模型以成本最优化为原则，目标函数如下：

3.3 决策方法

从上一节中可以看出，根据生产线间相似度对生产线进行分组是解决问题的首要关键，而不同的相似度标准可导致若干种类的生产线分组。在确定分组的基础上，确定相应分组下物流超市的四种成本总和，最后比较计算结果选出最优解。但是，在这种情况下，当汽车装配车间内生产线较多时，这种穷举法将出现计算困难的情况。因此，本文引入交叉相近计算法解决该问题。

从图1中可以看出，当物流超市的库存成本、投入与运营成本之和等于运输成本、缺货风险成本之和时，物流超市的总成本最小。但是，由于物流超市分散化程度呈离散型，因此，物流超市成本数值应该也呈离散型。根据公式：

可估算当穷举法中出现的结果逐渐向式（16）靠近时，该计算结果越接近最优解。同理，当库存成本、投入与运营成本之和与运输成本、缺货风险成本之和，两者差距越大，物流超市总物流成本越大。根据该原则，可以有效提高计算结果的计算速度，以减少冗余计算过程。

4 算例

以某汽车厂装配车间情况为例。该装配生产厂内共有三条生产线，分为L1，L2，L3。汽车装配车间零部件较多，但这里仅以若干零部件做代表，模拟实际装配车间运营状况进行数据的计算和分析。假设该装配车间共需12种零配件，其中P1-P7仅为生产线L1所需零件，P2-P5,P8-P10为生产线L2所需零件，P4,P5,P8,P9,P11,P12为生产线L3所需零件。根据公式（8），计算得该车间生产线间相似度矩阵见表1。

根据该相似度矩阵，可对三条生产线进行分组，可分为四种情况，见表2。

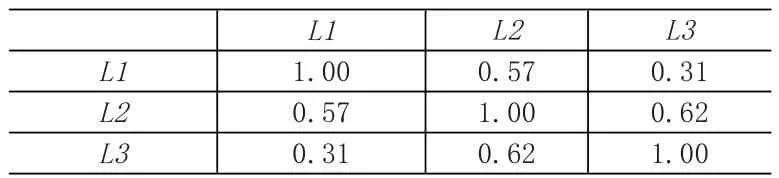
表1 装配生产线相似度矩阵

表2 生产线分组情况

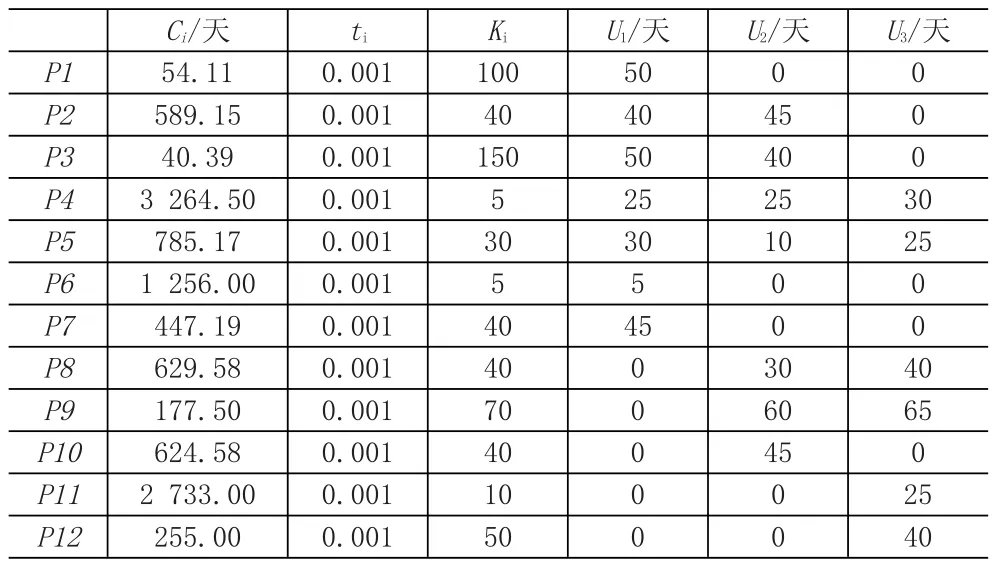
表3 各零部件基础参数表

对于求解中需要用到的固定值，这里做统一说明。其中，所有零部件提前运输时间LT均为1天；单位运输距离成本Co为0.18元；单个物流超市建设投入成本Ζ为1 200 000元；单个物流超市每年运营成本Ε为100 000元；这里假设每个物流超市的使用年限为10年，在计算物流超市的其他成本时也以10年的总量为准；表示单位缺货风险成本的Η为4 355元；表示缺货风险的影响因子α为1。对于物流超市的选址和位置关系，示例如表4、如图2所示。

表4 生产线与物流超市位置

图2 汽车装配生产线及物流超市分布举例

根据如上所列举的数据，按照第三节中的方法和步骤，可得到结果如下，见表5。

表5 不同分组下的物流超市成本

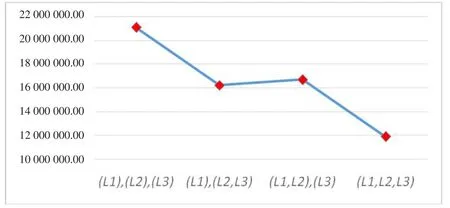
图3 不同分组情况的物流超市总成本对比

其中，第一种情况分组物流超市分散化程度最高，即(L1), (L2),(L3)的物流超市位置为A，B，C点；第二种情况分组物流超市分散化程度居中，即（L1），（L2,L3）的物流超市位置为A，E点；第三种情况分组与第二种情况相似，即（L1，L2），（L3）的物流超市位置为D，C点；第四种情况分组物流超市的分散化程度最低，即（L1，L2，L3）仅设置一个物流超市，其位置为B点。

根据以上结果可知，第四种情况，即仅设计一个物流超市的情况下，物流超市总成本最低，即在本例中，物流超市分散化程度最低为最优结果。

5 总结

本文基于物流成本的角度，考虑汽车装配车间内的物流超市分散化程度。本文首先在对物流超市成本结构与物流超市分散化程度之间的关系进行分析，把物流超市成本分为存货成本、投入与运营成本、运输成本和缺货风险成本。然后从物流超市的数量和位置两方面入手，引入装配生产线分组的概念，计算物流超市各项成本。最后得出使物流超市总成本最小的最优解，即基于多生产线情况的物流超市的最优分散化程度。然而，本文仍然存在很多局限性和不足。之后的研究可以针对更复杂的位置布局和更精准的分组方式角度进行研究，从而建立更完善的物流超市分散化决策模型。

[1]Persona A,Battini D,Manzini R,Pareschi A.Optimal safety stock 1evels of subassemblies and manufacturing component[J].Int J Prod Econ, 2007,110(1-2)：147-159.

[2]Daria Battine,Maurizio Faccio，Alessandro Persona.“Supermarket warehouse”:stocking policies optimization in an assembly-to-order environment[J].Int Ado MaufTechnol,2010,50:775-788．

[3]Akcay Y,Xu S H.Joint inventory replenishment and component allocation optimization in an assembly-to-order system[J].ManagSci,2004 50 (1):99-116．

[4]GolzJ,R Gujjula,H-O.Günther,S Rinderer,M Ziegler.Part feeding at high-variant mixed-model assembly lines[J].Flexible Services and Manufacturing Journal,2011,24:119-141.

[5]Emde S,and N.Boysen.Optimally locating in house logistics areas to facilitate JIT-supply of mixed-model assembly lines[J].International Journal of Production Economics,2012a,135:393-402.

[6]郑秀恋,刘陆.物流超市在汽车生产物流中的应用研究[J].物流技术,2013,32(7):80-85.

[7]俞杰.物流超市在工厂内部的应用[J].工业工程与管理,2004,(9): 131-133．

[8]Persona A,Battini D,Manzini R,Pareschi A.Optimal safety stock levels of subassemblies and manufacturing components[J].Int J Prod Econ, 2007,110(1-2):147-159.

Study on Decision Model for Distributiveness Degree of Logistics Supermarket for Automobile Assembly Workshops

Wang Ye,Zhang Jia,Cai Sanfa
(School of Economics&Management,Tongji University,Shanghai 200092,China)

In this paper,from the angle of logistics cost minimization,we analyzed the relationship of the distributiveness degree of the logistics supermarket for automobile assembly workshops with the different parts of the cost structure of the workshop,and then after introducing the concept of multiple production lines grouping,established the decision model for the distributiveness degree of the logistics supermarket.

logistics supermarket;distributiveness degree;logistics cost;multiple production lines;automobile assembly workshop

U468.22；F426.471

A

1005-152X(2015)10-0232-05

2015-08-30

王叶（1991-），女，辽宁人，硕士研究生，研究方向：物流与供应链管理；张镓（1975-），男，天津人，博士研究生，研究方向：物流与供应链管理；蔡三发（1973-），男，福建人，博士，研究员，研究方向：物流与供应链管理。

10.3969/j.issn.1005-152X.2015.10.062