电子和空穴掺杂CdO热电材料的第一性原理研究

张欣然（河北大学,物理科学与技术学院,河北省光电信息材料重点实验室,河北保定071002）

电子和空穴掺杂CdO热电材料的第一性原理研究

张欣然
（河北大学,物理科学与技术学院,河北省光电信息材料重点实验室,河北保定071002）

摘要：采用密度泛函理论下的第一性原理计算方法结合波尔兹曼输运理论，讨论不同电子和空穴掺杂浓度对CdO材料的电子结构及其热电输运特性的影响。通过能带结构以及态密度的计算，分析掺杂后CdO的导带底和价带顶在费米能级附近的变化情况;在高温区电子和空穴掺杂CdO的赛贝克系数的绝对值都是随温度的升高而升高。空穴掺杂后的载流子浓度比电子掺杂大,且空穴掺杂对CdO赛贝克系数的提高比电子掺杂要多。

关键词：第一性原理方法；热电材料；电子结构；赛贝克系数

热电材料是将热能与电能直接相互转换的一种环境友好型功能材料，在温差发电和制冷领域有着广阔的应用潜力，寻找并开发高性能的热电转换材料是当务之急。金属氧化物陶瓷材料引起了研究人员极大的兴趣，被认为是最具潜力的热电材料之一[1]。

氧化镉（CdO）是宽带隙的金属氧化物半导体材料，存在的氧空位和镉间隙缺陷使其具有较高的载流子浓度，具有优异电学性能，而被应用于平板显示装置以及光电子装置等领域[2]。本文中，利用波尔兹曼输运理论计算不同电子和空穴掺杂浓度的CdO赛贝克系数随温度的变化情况，这为理解CdO的热电输运性质及设计CdO基的热电材料提供了理论依据[3]。

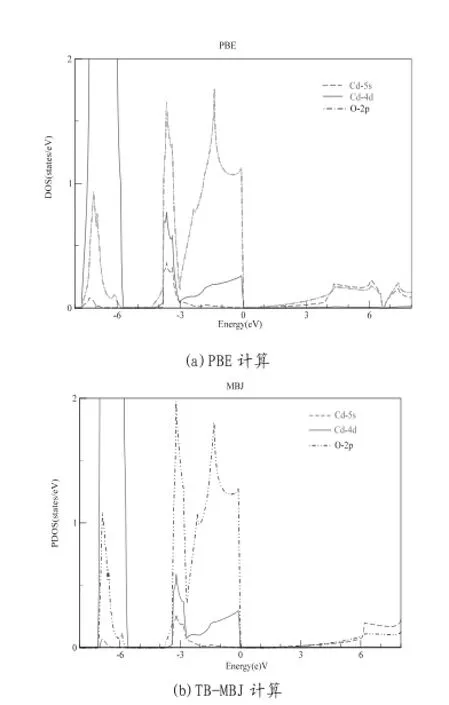
图1 本征CdO的分波态密度图

1计算方法

CdO属于面心立方结构，其空间群为Fm-3m，晶格常数为a=4.69Å。计算中采用基于密度泛函理下的第一性原理软件包（Wien2k）和基于波尔兹曼输运理论的基础上的BoltzTrap程序软件包，电子之间的交换关联势采用Tran和Blaha修正的Becke-Johnson（TB-MBJ）泛函，以进一步提高计算的精确度。对第一布里渊区采用54×54×54网格K点积分求和，进行自洽电子结构计算，停止后达到收敛[4]。

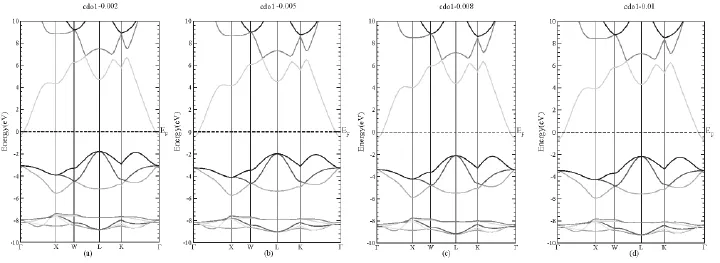
图2　不同电子掺杂浓度的CdO的能带结构

2CdO的电子结构

文中利用虚晶近似方法来模拟体系的不同电子和空穴掺杂浓度。图1（a-b）分别为采用广义梯度近似下的PBE关联泛函和TB-MBJ近似方法计算的本征CdO分波态密度图。从图1(a)中可以看出CdO是一种具有半金属特性的氧化物材料，经过TB-MBJ修正计算后得到的带隙展开，但仍低于实验值。观察图1(b),在价带的低能处(-7.18ev~-5.6ev)Cd3d电子态为主要贡献，O2p电子态的贡献较小，而在价带的高能态(-3.45ev~0ev)是Cd4d和O2p轨道杂化的共同作用。对于体系的导带部分，导带底的能带具有较大的展宽，主要是Cd5s和O2s、2p轨道重叠在一起的结果，且Cd5s态电子更靠近于导带[5-6]。

利用TB-MBJ交换关联泛函计算得到了不同电子和空穴掺杂浓度的CdO的能带图（如图2和图3）。图2中价带最高点在L点，导带最低点在处，CdO的能带结构显示为间接带隙，带隙大小约1.56eV，与实验值（2.26eV）相比偏小，这是密度泛函理论通常低估了半导体的带隙所致。图2（a-d）分别对应为CdO晶体原胞中掺入不同电子浓度(1.94×1019cm-3，4.85×1019cm-3，7.75×1019cm-3，9.69×1019cm-3)的能带图。从图可知，电子掺杂导致导带下移并穿过费米能级，使掺杂后的CdO呈现出N型半导体的特性。图3（a-d）分别为掺入不同空穴浓度（4.84×1020cm-3，9.69×1020cm-3，1.45×1021cm-3，1.94×1021cm-3）的能带图。相比于电子掺杂导致费米能级上移进入导带，空穴掺杂将会导致费米能级向下平移进入价带，CdO由原来的N型变为P型半导体材料[7]。随着空穴掺杂浓度的增加，CdO的费米能级向下移动的距离越大，穿过费米能级的空穴载流子越多。载流子浓度的增加导致赛贝克系数减小。因此，寻找合适的电子和空穴掺杂浓度，可以使CdO材料的优值达到最大。

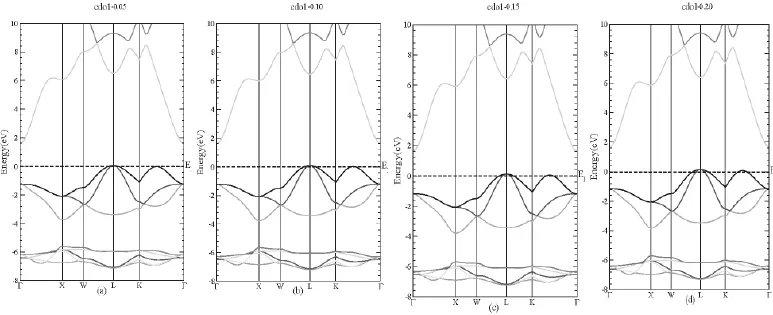
图3　不同空穴浓度掺杂CdO的能带结构图

3CdO的热电性质

图4和图5分别给出了不同电子和空穴掺杂浓度的CdO的赛贝克系数随温度(300～1000K)变化的曲线。从图4中可以看出掺杂电子后CdO的赛贝克系数为负值，为N型导电。在高温区，赛贝克系数的绝对值都是随着温度的升高而增加。当电子的掺杂浓度增加时，同一温度下的赛贝克系数的绝对值减小，最优掺杂电子浓度为1.94×1019cm-3,赛贝克系数值与载流子浓度呈反比。尽管载流子浓度增加导致材料的电导率增加，但对于金属氧化物热电材料，好的热电优值需要大的赛贝克系数和高的电导率以及低的热导率共同作用。图5中可以看出空穴掺杂后CdO的赛贝克系数为正值，是P型半导体。随着空穴掺杂浓度的增加，同一温度下的赛贝克系数将会减小。我们得到的最优掺杂空穴浓度为4.84×1020cm-3。

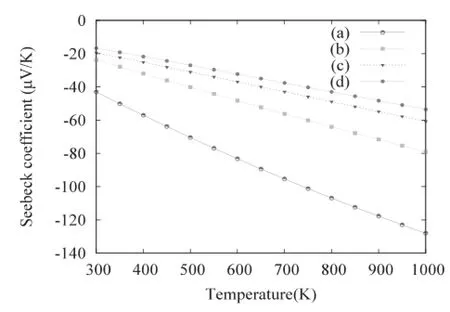
图4

不同电子（图4）和空穴（图5）掺杂浓度CdO的赛贝克系数随温度的变化规律。

在1000K时，最佳电子掺杂浓度为1.94×1019cm-3时的CdO晶体的赛贝克系数约为126，而最佳空穴掺杂浓度为4.84×1020cm-3时的CdO晶体赛贝克系数是其2倍多，约为250,因此空穴掺杂使CdO晶体赛贝克系数提高的更多。然而，本征CdO由于Cd间隙和O空位缺陷的存在而表现出N型半导体[7]。因此，提高CdO材料赛贝克系数的有效方法之一就是使CdO材料通过掺杂成为P型半导体。

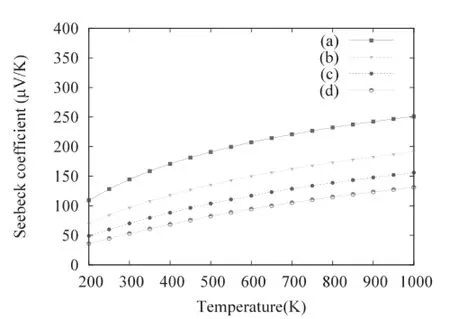
图5

4结论

本文利用第一性原理计算方法和波尔兹曼输运理论相结合，采用虚晶近似理论对CdO晶体进行不同浓度的电子和空穴掺杂，计算和讨论了它们的电子结构以及赛贝克系数随载流子浓度和温度的变化关系。结果表明：N型和P型CdO半导体的赛贝克系数都是随着温度的升高而升高，且随着载流子浓度的增加而降低。同时，空穴掺杂对CdO赛贝克系数的提高比电子掺杂对CdO赛贝克系数提高的更多，这对于提高CdO热电材料性能是一个可行的尝试，对发掘或设计新的热电材料具有很大的应用价值。

参考文献：

[1]NOUDEMJG,LEMONNIERS,PREVELM,etal.Thermoelectricceramicsforgenerators[J].JEurCeramSoc,2008,28(35):41-48.

[2]DOUY,EGDELLRG,LAWDS,etal.AnexperimentalandtheoreticalinvestigationoftheelectronicstructureofCdO[J]. JPhys:CondensMater,1998(10):8447-8458.

[3]唐鑫,吕海峰.Cd掺杂纤锌矿ZnO电子结构的第一性原理研究[J].物理学报,2008,57(02):1066-07.

[4]MADSENGKH,SINGHDJ,BOLTZTRAP.Acodeforcalculatingband-structuredependentquantities[J].ComputerPhysicsCom munications,2006,175(01):67-71.

[5]PENGFeng,LIUQiang,FUHongzhi,YANGXiangdong.First-principlescalculationsonphasetransitionandelasticityofCdOunderpressure[J].SolidStateCommunications,2008(148):6-9.

[6]CHENXin,PARKERD.Potentialthermoelectricperformanceofhole-dopedCu2O[J].NewJournalofPhysics,2013(15):043029.

[7]WONGCHAROENAN,GAEWDANGAT,WONGCHAROENBT.ElectricalPropertiesofAl-DopedCdOThinFilmsPreparedbyThermalEvaporationinVacuum[J].EnergyProcedia,2012(15):361-370.