大失准角SINS初始对准的UPF算法

王磊,万超（导航技术研究所,西安710068）

大失准角SINS初始对准的UPF算法

王磊,万超
（导航技术研究所,西安710068）

摘要：针对大失准角条件下捷联惯导系统（SINS）初始对准误差模型呈严重非线性的特点，设计了大失准角SINS的无迹粒子滤波（UPF）初始对准算法；并针对UPF算法实时性不强的特点，采用残差系统重采样对其重采样方法进行改进；再结合三轴转台静基座采集得到的实测数据，分别进行了UPF和无迹卡尔曼滤波（UKF）算法仿真，仿真结果表明：UPF算法比UKF算法具有更高的对准精度和更快的对准速度；改进后的UPF算法在对准精度上略差一些，但比原算法具有更强的实时性。

关键词：捷联惯导系统;大失准角;初始对准;UPF滤波;重采样

大失准角条件下，SINS初始对准误差模型呈线性化假设不再成立，线性姿态误差模型不再可用，于是使用传统的滤波方法进行初始对准状态估计受到局限。

目前，针对大失准角非线性误差模型，初始对准滤波方法主要有扩展卡尔曼滤波（EKF）、UKF、粒子滤波（PF）。EKF通过对非线性函数的泰勒级数展开式进行一阶线性化截断，从而将非线性问题转化为线性问题。但当非线性函数泰勒级数展开式的高阶项无法忽略时，EKF将导致很大的线性化误差，造成滤波器精度变低。文献[3]在大失准角SINS初始对准条件下推导了简化UKF算法，并通过仿真试验证明了算法的有效性。粒子滤波是英国学者Gorden等于1933年提出的。该算法能得到基于物理模型的近似最优数值解，而且简单实用，对系统的动态模型概率分布形式具有良好的鲁棒性，受滤波初始误差影响小，可适用于任何非线性系统模型，但随着算法的迭代会出现权值退化现象。文献[2]将EKF作为粒子滤波的重要性函数，证明了EPF算法在一定程度上解决了权值退化现象，而且具有比传统的EKF算法对准时间快，对准精度高的特点。

本文在粒子滤波的基础上通过将UKF作为其重要性分布函数来解决粒子退化问题，结合实测数据，研究比较UPF算法与UKF算法在SINS大失准角初始对准条件下的优劣性，并针对UPF算法实时性差的缺陷，使用残差系统重采样对其重采样方法进行改进，以达到提高实时性的目的。

1SINS大失准角误差模型

1.1SINS大失准角非线性状态误差方程̓̓

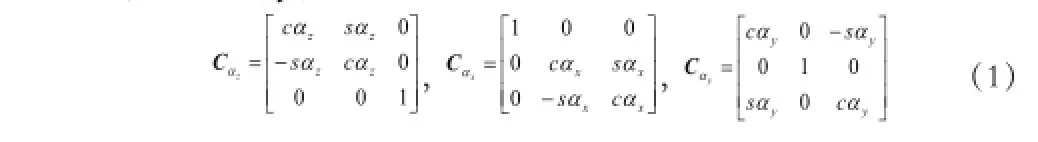
将（1）式三个矩阵逆序相乘得系至系的变换矩阵：̓̓

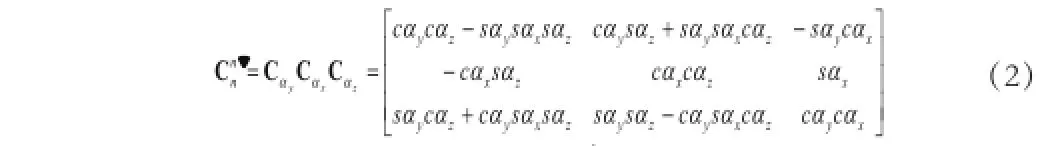
从而由（3）式得欧拉平台误差角微分方程：̓̓

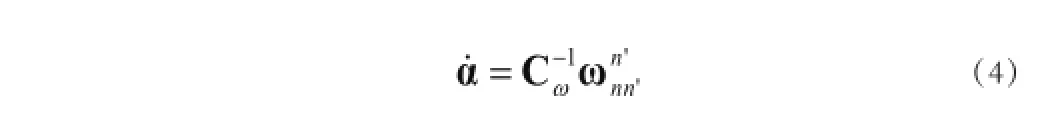
其中有：̓̓

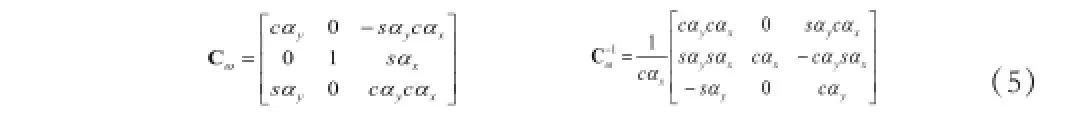
由（4）式，根据文献[3]，以欧拉平台误差角表示的SINS非线性姿态误差方程为: ̓̓

速度误差方程: ̓̓

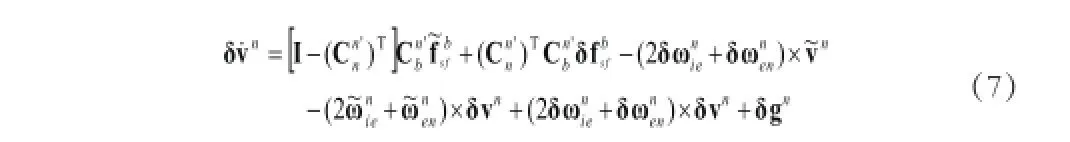
1.2静基座初始对准误差模型̓̓

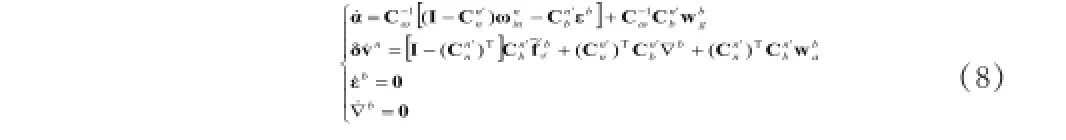
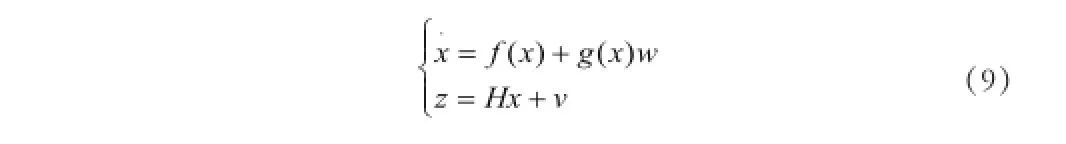
2UPF算法及其改进

2.1UPF算法̓̓

UPF算法是一种考虑到先验密度和观测信息的作用，把UKF和PF相结合的滤波方法，利用UKF实时的进行状态的均值和方差估计，以正态分布作为PF粒子采样的重要性函数，从而可以将采样粒子从高先验密度区向高似然密度区移动。其三个主要步骤是：产生新的粒子、计算粒子权重和重采样，解算主要流程如下：̓̓

（7）设定k=k+1，返回第2步。̓̓





UPF改进了一般PF滤波方法中重要性函数的选择方法，有利于将采样粒子从高先验密度区向高似然密度区移动，可以提高滤波精度。相对与一般PF滤波而言，UPF解算计算量有所增加，且同样需要重采样过程，所以在它具有良好的对准精度的同时，却不可避免的带来了实时性不强的缺点。

2.2UPF重采样方法及其改进̓̓

重采样是决定解决粒子权值退化问题和提高算法实时性的关键步骤。UPF算法中的重采样方法是系统重采样法，其算法代码简述

如下：̓

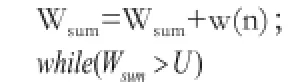
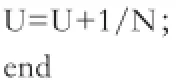
从上述代码可以看出，系统重采样通过循环比较Wsum与U值大小，来确定原粒子分解的个数。其中包含了两层循环和比较运算，所需要的存储空间为而残差系统重采样算法只需要一层循环，且无比较运算，其算法代码简述如下：̓

产生一个随机数U~u[0,1/N]；̓

forn=1:N ̓

i(n)=[(w(n)-U·n]+1；（[]为取整运算）

U=U+i（n)/N-w(n)；

end ̓̓

残差系统重采样的U值随机产生后并不进行累加运算，而是通过每次粒子分解结果进行调整，而且没有比较运算，所需要的存储空间为而且只需要一层循环，理论上提高了代码的运行效率，因此考虑用残差系统重采样方法代替原有重采样方法，可以提高UPF算法的实时性。将改进后的UPF称为IRUPF(improvedresamplingUPF)。

3仿真分析

仿真中实际量测数据由三轴转台静基座下采集获得。具体方法是：三轴转台归零（“东北天”位置）后，驱动内、中、外三个框都静止在5，开启光纤捷联系统，预热30min，室温条件下，以100Hz采样频率采集30min陀螺和加速度计数据。陀螺的随机漂移为，加速度计零偏和随机偏差都为，速度误差为0.1m/s，初始位置为[34.24.108.9,380]，状态初值x(0)均为0，失准角为，粒子数为200，仿真时间为10秒，时刻更新1000次，分别采用UKF和UPF仿真，并使用滤波结果闭环对速度和姿态进行修正，得到如下仿真结果见下图。

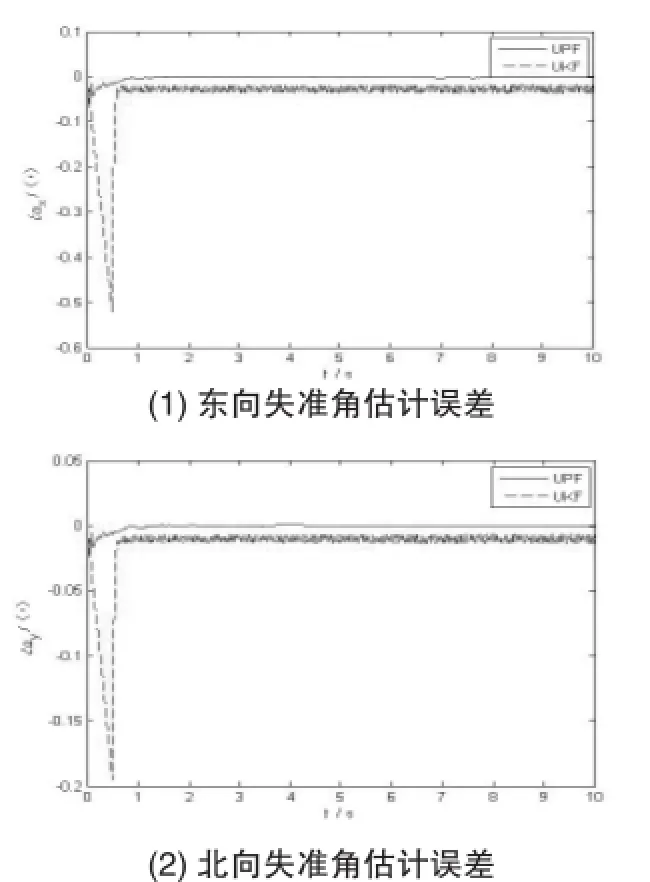
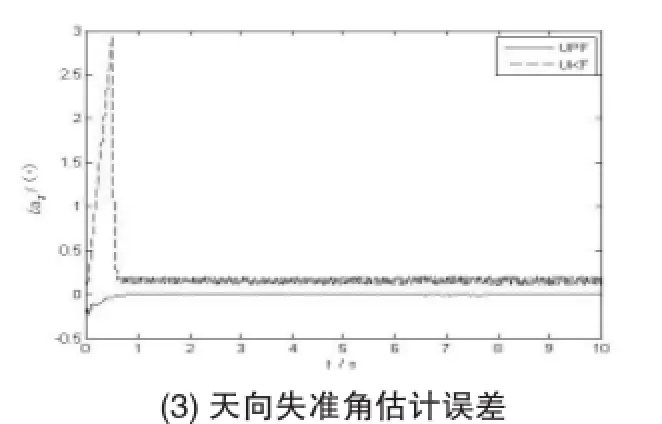
图1大失准角初始对准误差

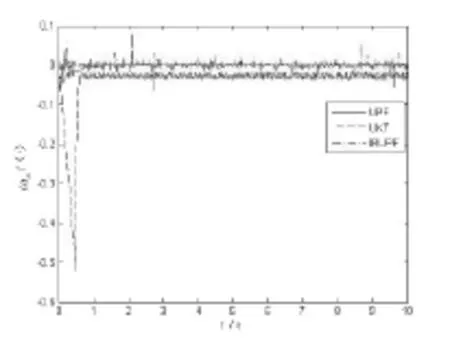
图2改进后的UPF在对准精度上和其他两种算法对比

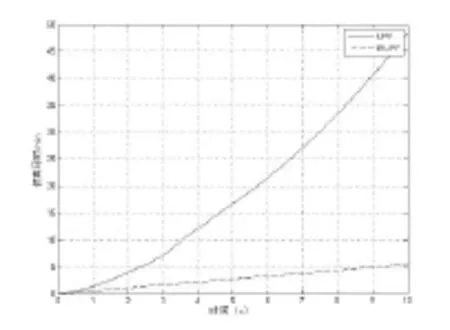
图3改进前后UPF算法在实时性上的对比

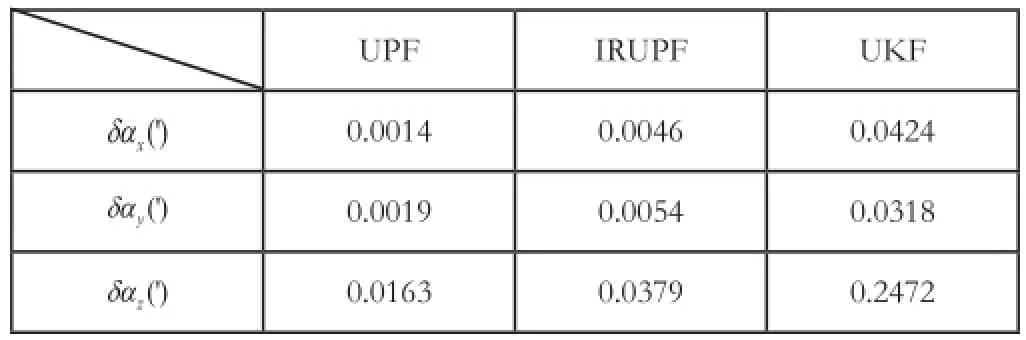
表1失准角估计的均方误差值

结合表1，从图1可以看出，在三个方向的对准精度上，UPF明显要高于UKF，在对准时间上，UPF在北向和东向失准角的第30次时刻更新时就已经开始进入收敛状态，而UKF要推迟到第70次时刻更新。即使在一般收敛速度比较慢的天向失准角上，UPF也保持了这种优越性。从图中还可以看出两种曲线收敛后，UPF的抗干扰能力要比UKF强，而且不易发散。

图2是IRUPF在对准精度上和其他两种算法的比较，介于篇幅，只给出东向误差仿真图。从表1中可以得出IRUPF在精度上要比UPF略差一些，而且从图1中可以看到IRUPF的毛刺比较多，但总体效果仍旧比UKF好，同时在图3中，UPF完成仿真需要近50分钟，而IRUPF只需要5分钟，很明显在实时性上IRUPF要优于UPF。在图3中，横坐标为代码设定的仿真时间，纵坐标为实际完成仿真所需时间，本文所采用的计算平台为Intel(R)CPUE65502.33GHZ,内存为1G，仿真软件为Matlab7.8.0。

另外，粒子数目越多，粒子滤波的精度就会越高。但是随着粒子数目的增加，迭代时刻的延长，就造成计算量增大，使得运算时间比较长，反而严重影响了初始对准的性能。在实际工作中，粒子数目的选择需在对准精度和实时性这两种性能之间做取舍。

4结论

文中将UKF作为PF的重要性分布函数，设计了大失准角SINS的无迹粒子滤波（UPF）初始对准算法。通过实测数据的试验仿真，验证了在状态方程为非线性，量测方程为线性的SINS大失准角条件的对准模型中，UPF算法在对准精度和对准时间上的有效性；并使用残差系统重采样对原始的UPF重采样方法进行改进，使得原UPF的重采样方法由两层循环变为一层，且舍去了比较运算，提高了代码运行效率，并通过试验仿真验证了改进后的算法极大的提高了初始对准的实时性。

参考文献：

[1]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西北工业大学出版社,1998.

[2]王志刚,陈良友,边少峰.EPF算法在惯导非线性初始对准中的应用[J].中国惯性技术学报,2007,15(02):165-166.

[3]严恭敏,严卫生,徐德民.简化UKF滤波在SINS大失准角初始对准中的应用[J].中国惯性技术学报,2008,16(03):364-368.

[4]JohnL.Crassidis,F.LandisMarkley.UnscentedFilteringforSpacecraftAttitudeEstimation[J].JournalofGuldanceandDynamics,2003,26(04):536-542.

[5]JulierSJ,UlmanJK.Uhlmann.Unscentedfilteringandnonlinearestimation[J].prodeedingsoftheIEEE,2004,92(03):401-422.

[6]冯池,赵娜,王萌.一种改进残差重采样算法研究[J].哈尔滨工程大学学报,2010,31(01):120-124.