λ－f域抛物Radon变换多次波压制方法

王维红，张 振，石 颖，李 莹

（东北石油大学地球科学学院，黑龙江大庆 163318）

λ－f域抛物Radon变换多次波压制方法

王维红，张 振，石 颖，李 莹

（东北石油大学地球科学学院，黑龙江大庆 163318）

空间截断效应降低传统Radon变换压制多次波的精度.提出一种λ－f域抛物Radon变换方法，与传统最小二乘抛物Radon变换相比，地震数据变换到λ－f域后表现为直线的映射，更便于设计滤波函数，从而有效消除传统多次波压制过程中空间截断效应的影响.另外，新变量λ的引入，使Radon正反算子成为与频率无关的矩阵，可大幅度提高计算效率.理论模型和实际海洋地震数据多次波压制试算结果表明，提出的λ－f域抛物Radon变换法可有效实现多次波压制，提高地震数据的信噪比，具有较强的实用性.

Radon变换；多次波压制；λ－f域；计算效率

0 引言

多次波压制是海洋地震资料处理中的重要预处理环节［1－4］，因为多次波的存在降低地震数据的分辨率，影响地震数据的成像质量［5－7］和后续地震解释的精度［8］，有效地压制多次波在地震数据处理中显得尤为重要.Radon变换是叠前地震数据处理中压制多次波的有效方法，人们研究Radon变换压制多次波的方法，Hampson D［9］提出频率域最小二乘抛物Radon变换方法，但是在Radon域存在剪刀状“拖尾”现象，致使滤波函数设计困难，从而导致多次波压制效果不理想.Sacchi M等［10］改进Hampson方法，提出频率域高分辨率抛物Radon变换方法；该方法在处理简单数据时可以有效地解决变换域“拖尾”现象，但对复杂介质的地震数据，无法得到高精度多次波压制效果.也有学者提出时间域Radon变换方法［11－12］弥补频率域Radon分辨率较低的缺陷，但时变矩阵的求解无法应用Levinson递推快速计算方法，导致计算效率大幅度降低.

笔者提出一种基于λ－f域抛物Radon变换压制多次波的方法，通过变量λ的引入，该方法的Radon变换算子与频率无关，从而比传统的Radon变换具有更高的计算效率［13］.同时，经λ－f域抛物Radon变换，抛物线型的地震同相轴在λ－f域变为具有一定斜率的直线，在一定程度上避免多次波压制过程中“拖尾”现象的干扰［14］.经过理论模型及实际地震资料的地震道集数据多次波压制试算，该方法具有较好的多次波压制效果.

1 最小二乘抛物Radon变换

抛物Radon正反变换时间域离散积分形式为

式（1－2）中：d（x，t）为时间—炮检距域地震数据；u（q，τ）为对应的Radon域的模型空间；q为曲率参数；τ为Radon域零偏移距截距时间；t为双程旅行时；Nx为地震数据的道数；Nq为曲率参数q的个数；xn为偏移距.

由于时间t与截距时间τ存在线性关系，可经由频率域高效计算抛物Radon变换，所以方程式（1）、（2）沿时间方向做傅里叶变换后，频率域形式表示为

式（3－4）中：u（q，f）、d（x，f）分别为u（q，τ）和d（x，t）对应的傅里叶变换；f为频率；j为虚数单位.对于单个频率成分，方程式（4）的矩阵形式为

其中，Radon算子为

由于L与LH不是互逆的，一般不直接采用算子LH计算Radon变换，而是采用最小二乘方法定义抛物Radon正变换，即

式中：I为单位矩阵；μ通常取LHL矩阵主对角线数据的0.01倍［15］，增强矩阵求解的稳定性.

式（5）、（7）即为正反Radon变换的关系式，由于式（5）、（7）中的Radon算子与频率有关，所以在式（5）、（7）求解过程中，每计算一个频率分量，需要计算一次Radon算子及算子的逆，降低计算效率.

2 λ－f域抛物Radon变换

定义新变量λ＝fq，式（4）在λ－f域的Radon变换定义为

式中：M为变量λ的个数.

与式（7）对应的λ－f域抛物Radon正变换为

其中，Radon算子L（λ）表达式为

λ－f域抛物Radon变换的算子L（λ）是关于偏移距参数xn及λ的复数矩阵，与频率无关，在整个λf域抛物Radon正反变换过程中仅需计算一次，相比于传统τ－q域抛物Radon变换，计算效率有很大程度的提高.并且LHL为主对角线元素相等的Toeplitz矩阵，所以Levinson递推法快速求解依然适用.

理论模拟炮记录的Radon变换域见图1.图1（a）为含有3个同相轴的单炮地震记录，共100道，道间距为20m，时间采样间隔为4ms，每道600个采样点.对图1（a）的地震数据采用最小二乘τ－q域抛物Radon正变换，理论上在Radon域得到3个点，然而实际上是3个含有很大假象的剪刀状的结果（“拖尾”现象）（见图1（b））.这是因为在Radon变换离散运算中，地震数据的有限孔径引起截断效应.在Radon变换压制多次波过程中，由于存在截断效应的干扰，有效波与多次波在Radon域的假象可能交织在一起，使得有效波与多次波的假象得不到完全分离，进而导致波场分离不彻底.

为消除空间截断效应的影响，对图1（a）的地震数据进行λ－f域抛物Radon变换，得到λ－f域剖面（见图1（c）），地震数据在经过λ－f域抛物Radon变换后，能量分布在以q为斜率的直线上，并未因空间截断效应在λ－f域产生假象，在一定程度上避免“拖尾”现象的干扰.

3 离散采样及滤波函数

3.1 离散采样

为避免在λ－f域抛物Radon变换过程中出现假频，对采样间隔参数Δλ和λ的范围进行合理离散采样，其中：

式（11－12）中：λmax、λmin分别为λ的最大和最小值；xmax、xmin分别为数据的最大和最小偏移距；ΔTmax、ΔTmin分别为地震数据在时空域的最大与最小动校正时差；fmax为数据最大有效频率.

3.2 滤波函数

根据λ定义，地震数据d在经过λ－f域抛物Radon变换后，一次波与多次波呈现过原点以不同曲率参数q为斜率的直线，引入滤波矩阵G（λ，f），对有效波和多次波进行分离.

式中：ΔT0为有效波与多次波分离所对应的动校正时差.有效波在λ－f域可表示为

变换到x－f域的有效波可表示为

4 数据试算

4.1 理论模型

为验证λ－f域抛物Radon变换在压制多次波中的有效性，合成含表面多次波的模型数据，见图2（a）.理论模型数据共100道，道间距为20m，时间采样间隔为4ms，每道601个采样点.分段部分动校正后的剖面见图2（b），一次波同相轴向上弯曲，曲率参数q为负值，为校正过量；多次波同相轴向下弯曲，曲率参数q为正值，为校正不足.地震数据在经过部分动校正后，有效波与多次波在变换域内得到更加有效的区分.对图2（b）的地震数据应用文中方法得到λ－f域剖面（见图2（c））.根据λ定义，一次波与多次波在λ－f域剖面上为经过原点且分布在原点两侧不同斜率的直线上.根据式（13）选取合适的滤波算子对图2（c）进行多次波切除，得到滤波后λ－f域剖面（见图2（d））.λ－f域剖面变换到时空域得到的单炮记录见图2（e），压制多次波后炮记录只有5个有效波同相轴，在图2（a）的其他多次波得到有效压制，即地震资料的信噪比得到有效提高.对理论模型数据应用最小二乘抛物Radon变换方法压制多次波后的剖面见图2（f），模拟的地震数据在1.8s处，有效波同相轴与多次波同相轴在时间域难以分开，在Radon变换域由于受空间截断效应的影响，两者的像在变换域也难以有效分开，所以影响滤波函数的设计，使最小二乘抛物Radon变换多次波压制的效果不理想，即多次波有较大残余能量，同时有效波的振幅也受到一定程度的损失.

图2 合成炮记录的多次波压制效果Fig.2 Multiple suppression result on synthetic shot record

4.2 实际地震数据多次波压制

为进一步测试文中方法在压制多次波中的稳定性和效果，对海洋地震数据进行多次波压制试算（见图3）.图3（a）为某工区海洋地震资料的一个CMP道集，数据共60道，道间距为50m，时间采样间隔为4 ms，时间方向8×103个采样点.图3（a）箭头在0.8s处的一阶表面多次波较为发育，应用λ－f域抛物Radon变换方法对该地震数据进行滤波处理，得到多次波压制后的道集记录见图3（b），能量很强的一阶表面多次波得到有效的压制，一次波的同相轴清晰可见，地震数据的信噪比得到有效提高，可为后续地震资料成像处理提供数据基础，实际数据的计算表明文中方法在压制海洋地震资料的多次波方面具有有效性和实用性.

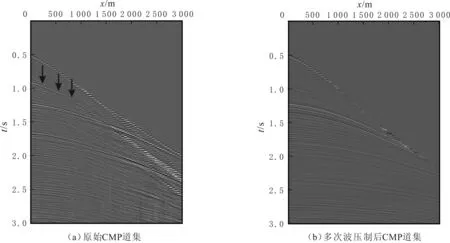
图3 实际数据多次波压制结果Fig.3 Multiple suppression result on field data

5 结论

（1）λ－f域抛物Radon变换通过引入新变量λ，Radon算子的特点和传统最小二乘方法不同，其正反算子仅需计算一次，大幅提高该方法的计算效率.

（2）抛物线型同相轴在λ－f域抛物Radon变换域为过原点的具有一定斜率的直线，在一定程度上避免传统抛物Radon变换压制多次波过程中空间截断效应的影响，并且其多次波压制滤波函数的设计也更为简单.

（3）应用λ－f域抛物Radon变换可有效提高地震数据的信噪比，具有稳定、有效和实用的特点.

（References）：

［1］ 薛东川.几种叠前逆时偏移成像条件的比较［J］.石油地球物理勘探，2013，48（2）：222－227.

Xue Dongchuan.Comparison of several imaging condition for prestack reverse－time migration［J］.Oil Geophysical Prospecting，2013，48（2）：222－227.

［2］ 马继涛，Sen M K，陈小宏.平面波域反数据处理压制多次波方法研究［J］.地球物理学报，2009，52（3）：808－816.

Ma Jitao，Sen M K，Chen Xiaohong.Multiple attenuation using inverse data processing in the plane－wave domain［J］.Chinese Journal of Geophysics，2009，52（3）：808－816.

［3］ 刘伊克，Sun Hongchuan，常旭.基于波射线路径偏移压制多次波［J］.地球物理学报，2004，47（4）：697－701.

Liu Yike，Sun Hongchuan，Chang Xu.Multiple removal by wavepath migration［J］.Chinese Journal of Geophysics，2004，47（4）：697－701.

［4］ 熊登，赵伟，张剑锋.混合域高分辨率抛物Radon变换及在衰减多次波中的应用［J］.地球物理学报，2009，52（4）：1068－1077.

Xiong Deng，Zhao Wei，Zhang Jianfeng.Hybrid－domain high－resolution parabolic Radon transform and its application to demultiple［J］.Chinese Journal of Geophysics，2009，52（4）：1068－1077.

［5］ 郭雪豹，王建民，王维红，等.基于GPU并行加速的VSP数据逆时偏移［J］.东北石油大学学报，2014，38（2）：58－62.

Guo Xuebao，Wang Jianmin，Wang Weihong，et al.VSP data reverse－time migration based on GPU parallel acceleration［J］.Journal of Northeast Petroleum University，2014，38（2）：58－62.

［6］ 石颖，陆加敏，柯璇，等.基于GPU并行加速的叠前逆时偏移方法研究［J］.东北石油大学学报，2012，36（4）：111－115.

Shi Ying，Lu Jiamin，Ke Xuan，et al.Prestack reverse time migration based on GPU parallel accelerating algorithm［J］.Journal of Northeast Petroleum University，2012，36（4）：111－115.

［7］ 田东升，王云专，李义鹏，等.单程和双程波动方程叠前深度偏移方法［J］.东北石油大学学报，2014，38（4）：39－44.

Tian Dongsheng，Wang Yunzhuan，Li Yipeng，et al.One－way and two－way wave equation pre－stack depth migration approaches［J］.Journal of Northeast Petroleum University，2014，38（4）：39－44.

［8］ 张进铎.地震解释技术现状及发展趋势［J］.地球物理学进展，2006，49（2）：578－587.

Zhang Jinduo.Present status and future trend of seismic data interpretation techniques［J］.Progress in Geophysics，2006，49（2）：578－587.

［9］ Hampson D.Inverse velocity stacking for multiple elimination［J］.Journal of the Canadian Society of Exploration Geophysicists，1986，22（1）：44－55.

［10］ Sacchi M，Ulrych T.High－resolution velocity gather and offset space reconstruction［J］.Geophysics，1995，60（4）：1169－1177.

［11］ Trad D，Ulrych J，Sacchi M.Accurate interpolation with high－resolution time－variant Radon transform［J］.Geophysics，2002，67（2）：644－656.

［12］ Ng M，Perz M.High resolution Radon transform in the t－x domain using"intelligent"prioritization of the Gauss－Seidel estimation sequence［J］.G xandd Abra，2004，18（3）：260－263.

［13］ 石颖，张振，李婷婷，等.λ－f域加权抛物Radon变换地震数据重建方法研究［J］.地球物理学进展，2014，29（4）：1752－1757.

Shi Ying，Zhang Zhen，Li Tingting，et al.Investigation on seismic data reconstruction by domain weighted parabolic Radon transform method［J］.Progress in Geophysics，2014，29（4）：1752－1757.

［14］ 谢俊法，孙成禹，韩文功.迭代抛物Radon变换法分离一次波与多次波［J］.石油地球物理勘探，2014，49（1）：76－81.

Xie Junfa，Sun Chengyu，Han Wengong.Iterative parabolic Radon transform for primary and multiple separations［J］.Oil Geophysical Prospecting，2014，49（1）：76－81.

［15］ Schonewille M A，Duijndam A J W.Parabolic Radon transform，sampling and efficiency［J］.Geophysics，2001，66（2）：667－678.

DOI 10.3969／j.issn.2095－4107.2015.01.003

TE132.1，P631

A

2095－4107（2015）01－0017－06

2014－12－01；编辑：陆雅玲

国家自然科学基金项目（41474118）；国家高技术研究发展计划（863计划）项目（2012AA061202）

王维红（1975－），男，博士，副教授，主要从事地震资料数字处理方面的研究.